Стандартные метрические пространства
Похожие статьи вашей тематики
1. 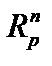 – n-мерное арифметическое пространство с радикальной метрикой. При – n-мерное арифметическое пространство с радикальной метрикой. При 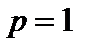  (проверка неравенства треугольника: (проверка неравенства треугольника:  ) При ) При 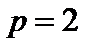 метрику метрику 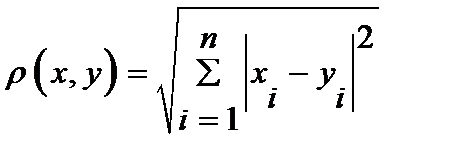 называют называют  евклидовой, а пространство евклидовой, а пространство 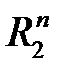 - арифметическим n -мерным пространством. - арифметическим n -мерным пространством.
2.  – –  -мерное арифметическое пространство с супремальной метрикой. -мерное арифметическое пространство с супремальной метрикой.
3. 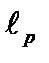 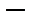 пространство ограниченных последовательностей с радикальной метрикой пространство ограниченных последовательностей с радикальной метрикой 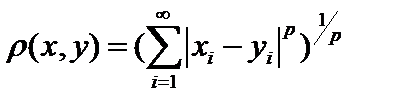 . При . При 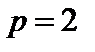 это такие последовательности, сумма квадратов элементов которых конечна (то есть ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно (координатное гильбертово пространство). это такие последовательности, сумма квадратов элементов которых конечна (то есть ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно (координатное гильбертово пространство).
4.  или или  или или 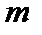  пространство ограниченных последовательностей с супремальной метрикой. пространство ограниченных последовательностей с супремальной метрикой.
5. 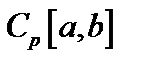  пространство непрерывных функций с радикальной метрикой. Его пополнение пространство непрерывных функций с радикальной метрикой. Его пополнение  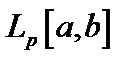 - лебегово пространство.Метрика пространстваЛебега - лебегово пространство.Метрика пространстваЛебега  : :  . При . При 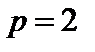 пространство пространство 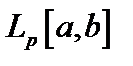 гильбертово и обозначается как гильбертово и обозначается как 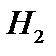 . .
6. 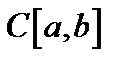 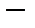 пространство непрерывных функций с супремальной метрикой (чебышевское). пространство непрерывных функций с супремальной метрикой (чебышевское).
7. 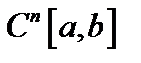 или или  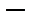 пространство пространство 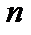 раз непрерывно дифференцируемых функций с супремальной метрикой (такая метрика называется дифференциальной): раз непрерывно дифференцируемых функций с супремальной метрикой (такая метрика называется дифференциальной): 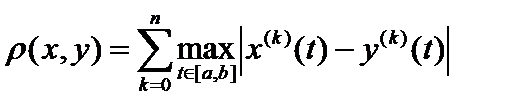 . .
8.   пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение 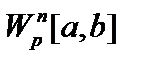  пространства Соболева.Метрика пространств Соболева пространства Соболева.Метрика пространств Соболева 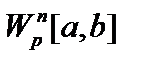 : :  . При . При 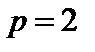 пространство пространство  гильбертово и обозначается как гильбертово и обозначается как  . .
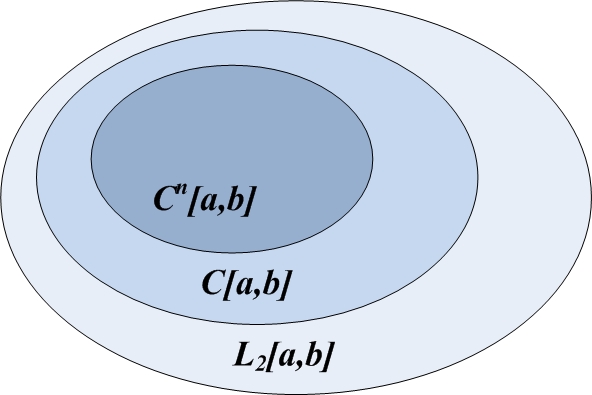
Комментарий. Будем говорить, что пространство X вложено в пространство Y, если все элементы пространства X принадлежат Y, то есть 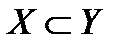 .На рисунке схематично изображено взаимное соотношение между основными пространствами функций. Самое широкое пространство — пространство суммируемых с квадратом функций, самое узкое — пространство .На рисунке схематично изображено взаимное соотношение между основными пространствами функций. Самое широкое пространство — пространство суммируемых с квадратом функций, самое узкое — пространство 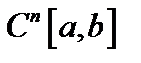 . В математике используются не только эти, наиболее употребительные, но и другие типы пространств, которые могут быть шире или уже рассмотренных пространств, а могут занимать и некоторое промежуточное положение. . В математике используются не только эти, наиболее употребительные, но и другие типы пространств, которые могут быть шире или уже рассмотренных пространств, а могут занимать и некоторое промежуточное положение.
Пример 1. На плоскости 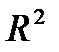 для точек для точек 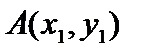 и и 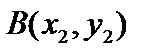 определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом. определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.
1.Метрика  . Это евклидова метрика при . Это евклидова метрика при 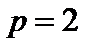  . .
 Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки 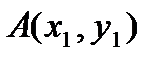 , ,  , , 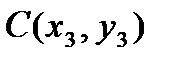 и докажем следующее неравенство: и докажем следующее неравенство:
 . .
Возведем это неравенство в квадрат:
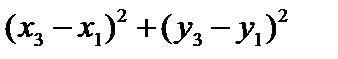 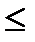 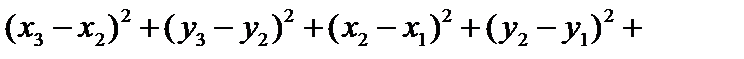
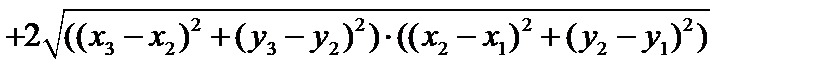 . .
Так как 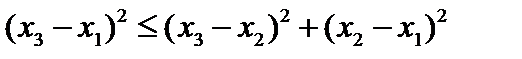 и и  (поскольку (поскольку 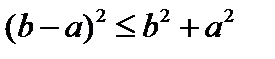 ) и выражение ) и выражение 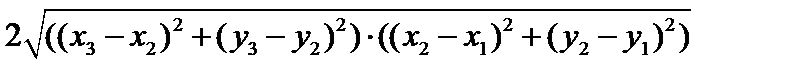 есть величина неотрицательная, то неравенство является верным. есть величина неотрицательная, то неравенство является верным.
2. Метрика  .Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки .Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки 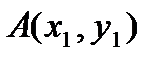 , ,  , , 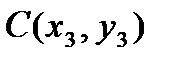 и докажем следующее неравенство: и докажем следующее неравенство: 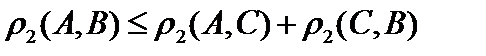 . .
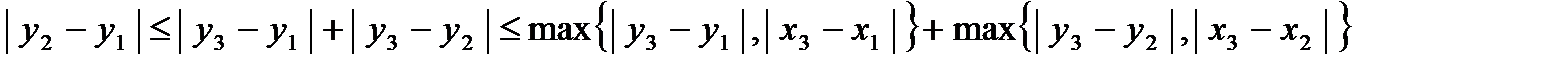 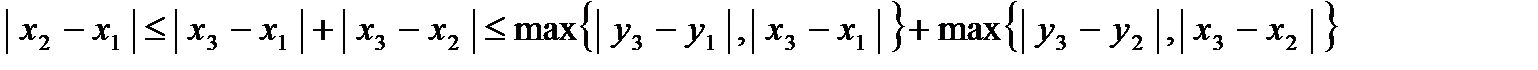 Тогда и Тогда и 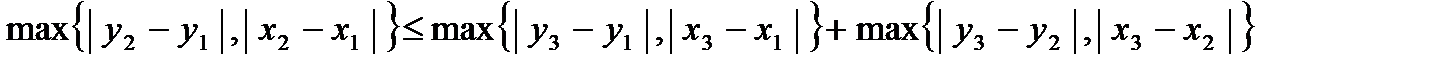 . .
3. Метрика 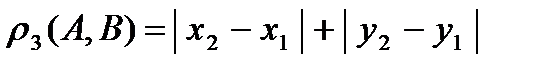 . Это двумерное арифметическое пространство с радикальной метрикой при . Это двумерное арифметическое пространство с радикальной метрикой при 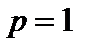 . Такую метрику называют манхеттенской, но можно назвать и таганрогской, потому что исторически вторым после Нью-Йорка городом мира с линейной, а не круговой системой улиц, был Таганрог. Кратчайшее расстояние между точками . Такую метрику называют манхеттенской, но можно назвать и таганрогской, потому что исторически вторым после Нью-Йорка городом мира с линейной, а не круговой системой улиц, был Таганрог. Кратчайшее расстояние между точками  и и 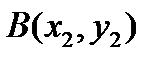 такого города будет определяться формулой такого города будет определяться формулой  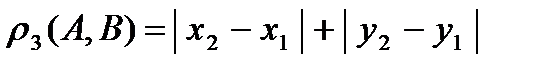 . .
Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки 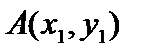 , ,  , , 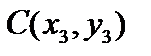 . Неравенство: . Неравенство:  - очевидно. - очевидно.
Комментарий. 1.Понятие пополнения употреблено впрок и будут определено позднее.
2. Любое нормированное пространство является метрическим с метрикой 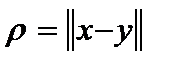 . Выполнение первых аксиом очевидно. Третья выполняется в силу . Выполнение первых аксиом очевидно. Третья выполняется в силу 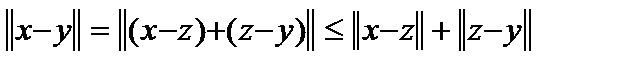 . Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть . Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть 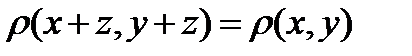 и однородностью относительно растяжений, то есть и однородностью относительно растяжений, то есть  , то тогда верно и обратное и норма элемента есть метрика, второй элемент которой есть ноль. , то тогда верно и обратное и норма элемента есть метрика, второй элемент которой есть ноль.
Для стандартных метрических пространств это так, так что все вышеприведённые примеры являются одновременно и примерами стандартных норм с геометрией, отличной от эвклидовой. Единичные шары в этих метриках изображены в примере 3.
Пример 2. Покажем, что  является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы
проверить третью, то есть 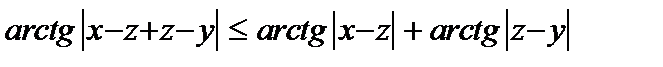 , докажем, что для любых , докажем, что для любых 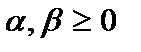 имеет место неравенство имеет место неравенство 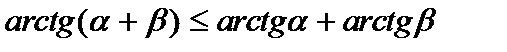 . .
Для этого зафиксируем 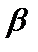 и рассмотрим функцию и рассмотрим функцию  . Так как . Так как 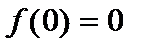 , а , а  , то , то 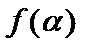 возрастающая функция. Однако, метрика возрастающая функция. Однако, метрика 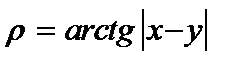 при при 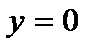 не будет нормой, так как не будет нормой, так как 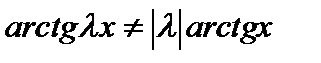 . . 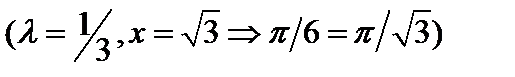 . .
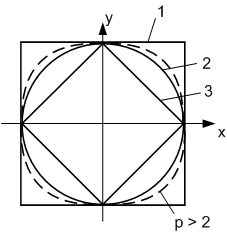
Пример 3. Рассмотрим пространство  . Положив . Положив  , а , а 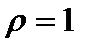 , мы получим единичную сферу в пространстве , мы получим единичную сферу в пространстве  . .
При  уравнение этой сферы имеет вид: ||x||1 = |x| + |y| и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае уравнение этой сферы имеет вид: ||x||1 = |x| + |y| и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае 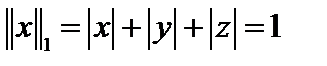 будет октаэдр. будет октаэдр.
При  уравнение этой сферы имеет вид: ||x||2 = (|x|2 + |y|2)1/2 – и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера. уравнение этой сферы имеет вид: ||x||2 = (|x|2 + |y|2)1/2 – и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.
Чебышёвская (кубическая) метрика: ||x||∞=max{|x|,|y|}, потому что единичной сферой в трёхмерном случае  будет куб. будет куб.
На рисунке: 1  чебышёвская(кубическая) метрика; 2 чебышёвская(кубическая) метрика; 2  евклидова (сферическая) метрика; 3 евклидова (сферическая) метрика; 3  октаэдрическая метрика. Случай октаэдрическая метрика. Случай  изображен пунктиром. При изображен пунктиром. При 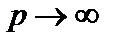 гёльдеровская группа метрик стремится к чебышевской. гёльдеровская группа метрик стремится к чебышевской.
Примеры. 1. Пространство изолированных точек (дискретное пространство): 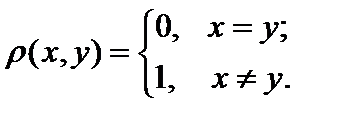 Здесь Здесь   любое непустое множество. любое непустое множество.
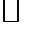 Первые две аксиомы очевидны. Проверим третью. Первые две аксиомы очевидны. Проверим третью.
 Пусть неверно, что Пусть неверно, что 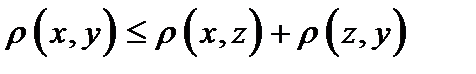 . Тогда . Тогда  Но тогда Но тогда 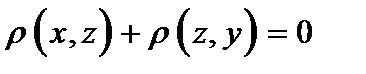 , то есть , то есть  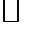
2. Ограниченные последовательности 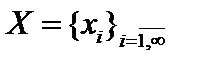 , с метрикой , с метрикой 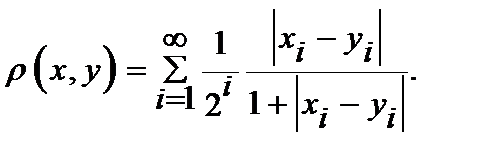
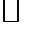 Проверим третью аксиому. Рассмотрим возрастающую функцию Проверим третью аксиому. Рассмотрим возрастающую функцию  .Так как .Так как  , то , то  , то есть , то есть 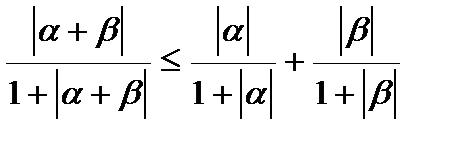 . Пусть . Пусть 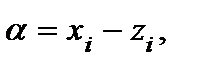  , тогда , тогда  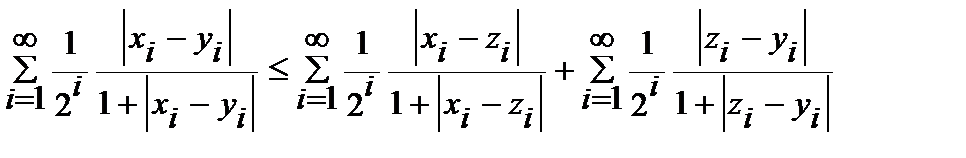 , или , или  
Комментарий. Пусть 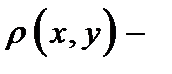 метрика на носителе метрика на носителе 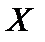 .Тогда .Тогда 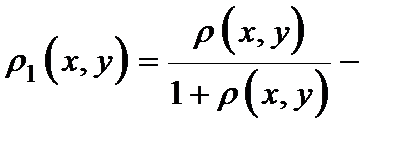 тоже метрика на носителе тоже метрика на носителе 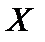 . Это позволяет дать . Это позволяет дать
Определение. Пусть 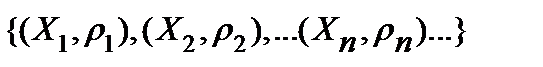  последовательность метрических пространств. Прямым (декартовым) произведением этих метрических пространств называется пара последовательность метрических пространств. Прямым (декартовым) произведением этих метрических пространств называется пара  , где , где 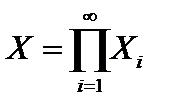 , а , а 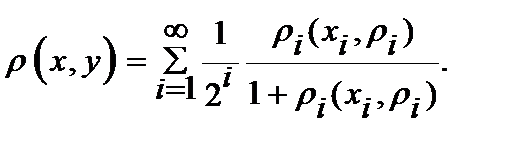
3. Показать, что пара 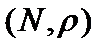 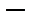 метрическое пространство, если метрика на носителе метрическое пространство, если метрика на носителе 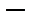 натуральных числах натуральных числах 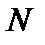 задана так: задана так: 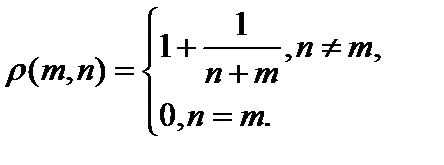 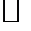 Неравенство треугольника для несовпадающих точек Неравенство треугольника для несовпадающих точек 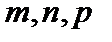 очевидно: очевидно: 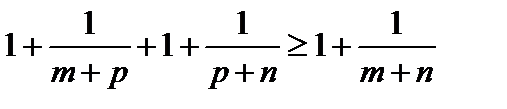 . .  В этой метрике при В этой метрике при  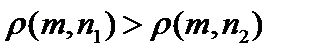 то есть натуральные числа чем дальше они расположены на числовой оси, тем ближе по метрике то есть натуральные числа чем дальше они расположены на числовой оси, тем ближе по метрике 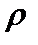 . .
4. Является ли метрикой функция а)  ; ;
б)  ; в) ; в) 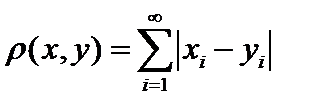 на множестве ограниченных последовательностей? на множестве ограниченных последовательностей?
5. В пространстве 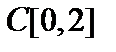 найти расстояние между функциями а) найти расстояние между функциями а) 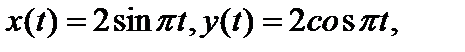 ( (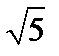 ); б) ); б) 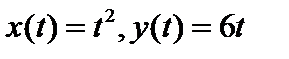 (8); (8);
в) 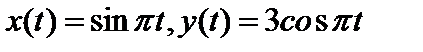 (5); г) (5); г) 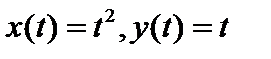 ( ( ). ).
6. В пространствах  найти расстояние между функциями найти расстояние между функциями 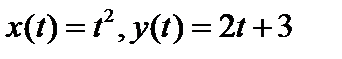 . .
7. В пространствах 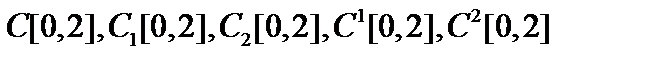 найти расстояние между функциями а) найти расстояние между функциями а)  ; б) ; б) 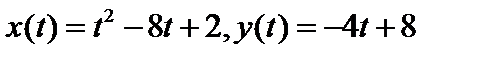 . .
8. В пространствах 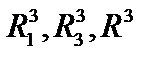 найти нормы элементов найти нормы элементов 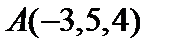 и и 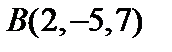 и расстояние между ними. и расстояние между ними.
9. В пространствах 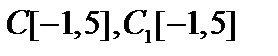 найти норму элемента найти норму элемента 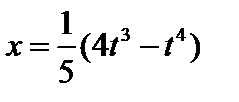 . .
10. Показать, что пространство 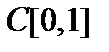 не гильбертово. не гильбертово.
 Пространство Пространство 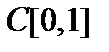 полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма полное нормированное пространство, то есть банахово. (Полноту покажем в следующем пункте.) Уже отмечалось, что норма порождается скалярным произведением, если и только если выполняется равенство параллелограмма 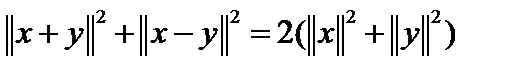 . Пусть . Пусть 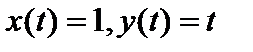 .Тогда, вычисляя норму в пространстве .Тогда, вычисляя норму в пространстве 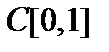 , сразу получим , сразу получим  
11. Можно ли в качестве нормы в пространстве 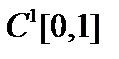 использовать норму пространства использовать норму пространства 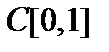 ? ?  Проверим аксиоматику. Проверим аксиоматику.
1. 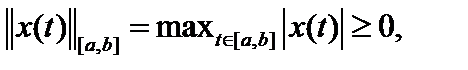 причём причём 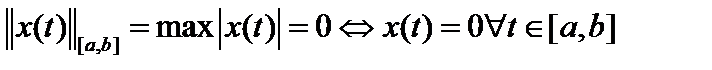 . 2. . 2.  . .
3. 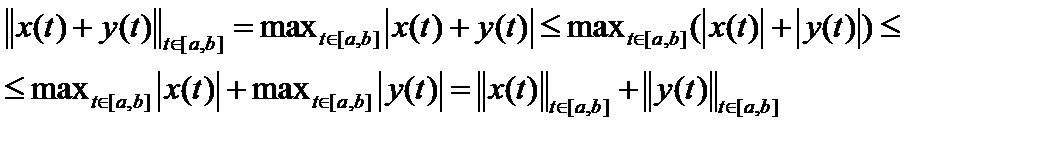
12. Можно ли в качестве нормы в пространстве 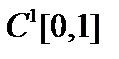 использовать норму использовать норму 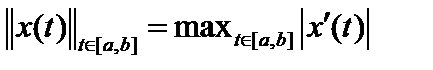 ? ? 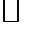 Нет, так как не выполняется первая аксиома нормы: Нет, так как не выполняется первая аксиома нормы: 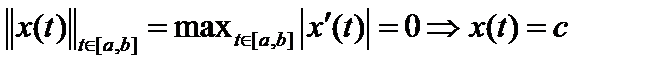 , где , где 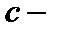 произвольная константа. произвольная константа.
13. Доказать, что подпространство 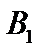 банахова пространства банахова пространства 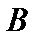 является банаховым пространством. является банаховым пространством.
 Пусть последовательность Пусть последовательность  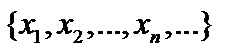 фундаментальна в подпространстве фундаментальна в подпространстве 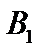 банахова пространства банахова пространства 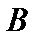 (нормы, естественно, одинаковы). Эта последовательность является фундаментальной и в (нормы, естественно, одинаковы). Эта последовательность является фундаментальной и в 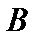 , так как , так как 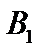 подпространство. Но подпространство. Но 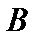 – банахово, то есть – банахово, то есть 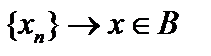 . Так как . Так как 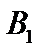 – –
подпространство, то по определению подпространства оно замкнуто,
следовательно, 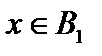 . Таким образом, произвольная фундаментальная последовательность в подпространстве . Таким образом, произвольная фундаментальная последовательность в подпространстве 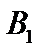 сходится к сходится к 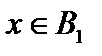 .А это значит, что .А это значит, что 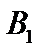  банахово по определению. банахово по определению. 
|



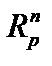 – n-мерное арифметическое пространство с радикальной метрикой. При
– n-мерное арифметическое пространство с радикальной метрикой. При 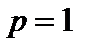
 (проверка неравенства треугольника:
(проверка неравенства треугольника:  ) При
) При 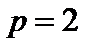 метрику
метрику 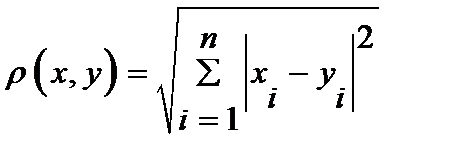 называют
называют  евклидовой, а пространство
евклидовой, а пространство 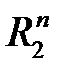 - арифметическим n -мерным пространством.
- арифметическим n -мерным пространством. –
–  -мерное арифметическое пространство с супремальной метрикой.
-мерное арифметическое пространство с супремальной метрикой.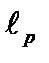
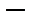 пространство ограниченных последовательностей с радикальной метрикой
пространство ограниченных последовательностей с радикальной метрикой 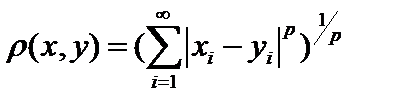 . При
. При 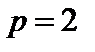 это такие последовательности, сумма квадратов элементов которых конечна (то есть ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно (координатное гильбертово пространство).
это такие последовательности, сумма квадратов элементов которых конечна (то есть ряд сходится). Эту сумму квадратов, т.е. сумму ряда, назовем квадратом длины вектора. Операции сложения и умножения на число определим как для конечномерных векторов-столбцов, то есть поэлементно (координатное гильбертово пространство). или
или  или
или 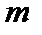
 пространство ограниченных последовательностей с супремальной метрикой.
пространство ограниченных последовательностей с супремальной метрикой.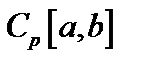
 пространство непрерывных функций с радикальной метрикой. Его пополнение
пространство непрерывных функций с радикальной метрикой. Его пополнение 
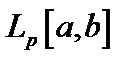 - лебегово пространство.Метрика пространстваЛебега
- лебегово пространство.Метрика пространстваЛебега  :
:  . При
. При 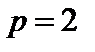 пространство
пространство 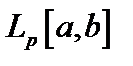 гильбертово и обозначается как
гильбертово и обозначается как 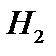 .
.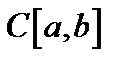
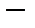 пространство непрерывных функций с супремальной метрикой (чебышевское).
пространство непрерывных функций с супремальной метрикой (чебышевское).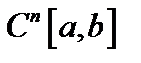 или
или 
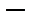 пространство
пространство 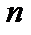 раз непрерывно дифференцируемых функций с супремальной метрикой (такая метрика называется дифференциальной):
раз непрерывно дифференцируемых функций с супремальной метрикой (такая метрика называется дифференциальной): 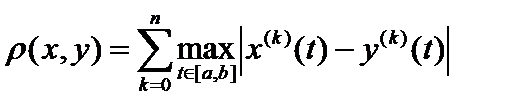 .
.
 пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение
пространства непрерывно дифференцируемых функций с радикальной метрикой. Их пополнение 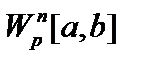
 пространства Соболева.Метрика пространств Соболева
пространства Соболева.Метрика пространств Соболева 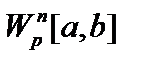 :
:  . При
. При 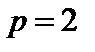 пространство
пространство  гильбертово и обозначается как
гильбертово и обозначается как  .
.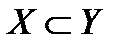 .На рисунке схематично изображено взаимное соотношение между основными пространствами функций. Самое широкое пространство — пространство суммируемых с квадратом функций, самое узкое — пространство
.На рисунке схематично изображено взаимное соотношение между основными пространствами функций. Самое широкое пространство — пространство суммируемых с квадратом функций, самое узкое — пространство 
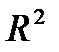 для точек
для точек 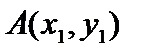 и
и 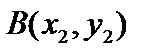 определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом.
определим расстояние тремя различными способами и покажем, что введенные расстояния являются метриками, то есть проверим выполнимость аксиом. . Это евклидова метрика при
. Это евклидова метрика при  .
. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки
Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки 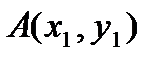 ,
,  ,
, 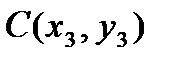 и докажем следующее неравенство:
и докажем следующее неравенство: .
.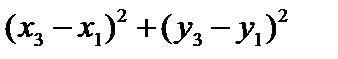
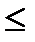
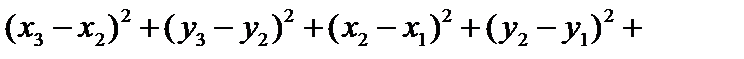
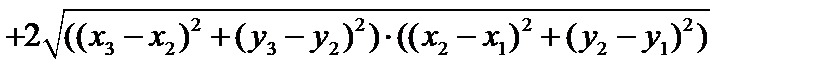 .
.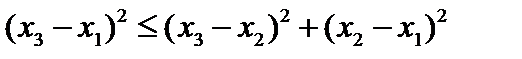 и
и  (поскольку
(поскольку 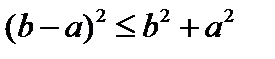 ) и выражение
) и выражение 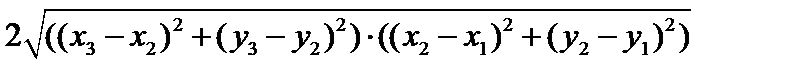 есть величина неотрицательная, то неравенство является верным.
есть величина неотрицательная, то неравенство является верным. .Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки
.Это двумерное арифметическое пространство с супремальной метрикой. Первые аксиомы очевидны. Проверим третью аксиому. Рассмотрим точки 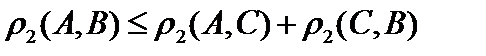 .
.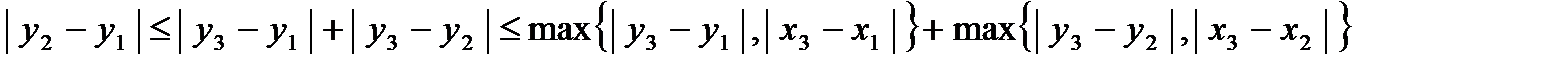
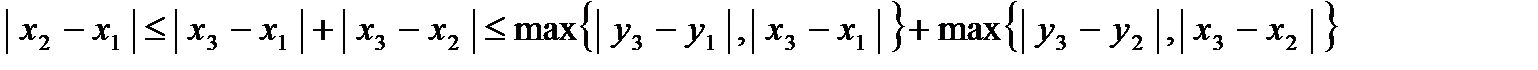 Тогда и
Тогда и 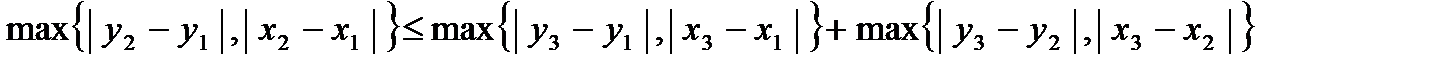 .
.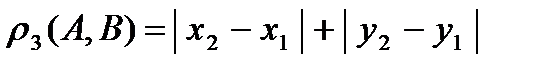 . Это двумерное арифметическое пространство с радикальной метрикой при
. Это двумерное арифметическое пространство с радикальной метрикой при  и
и 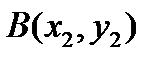 такого города будет определяться формулой
такого города будет определяться формулой 
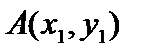 ,
,  ,
, 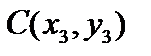 . Неравенство:
. Неравенство:  - очевидно.
- очевидно.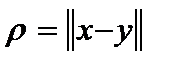 . Выполнение первых аксиом очевидно. Третья выполняется в силу
. Выполнение первых аксиом очевидно. Третья выполняется в силу 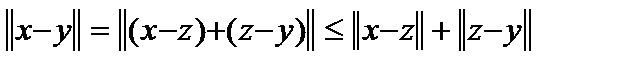 . Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть
. Обратное, вообще говоря, неверно, то есть метрические пространства, вообще говоря, не являются нормированными. Но если потребовать, чтобы метрическое пространство обладало инвариантностью относительно сдвигов, то есть 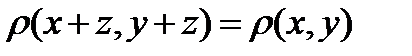 и однородностью относительно растяжений, то есть
и однородностью относительно растяжений, то есть  , то тогда верно и обратное и норма элемента есть метрика, второй элемент которой есть ноль.
, то тогда верно и обратное и норма элемента есть метрика, второй элемент которой есть ноль. является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы
является метрикой. Выполнение первых двух аксиом метрики очевидно. Чтобы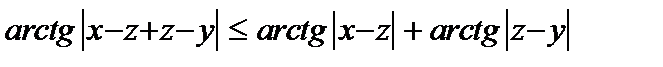 , докажем, что для любых
, докажем, что для любых 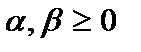 имеет место неравенство
имеет место неравенство 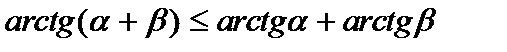 .
.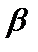 и рассмотрим функцию
и рассмотрим функцию  . Так как
. Так как 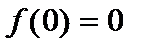 , а
, а  , то
, то 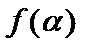 возрастающая функция. Однако, метрика
возрастающая функция. Однако, метрика 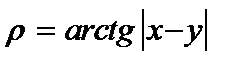 при
при 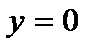 не будет нормой, так как
не будет нормой, так как 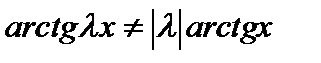 .
. 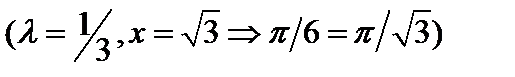 .
. . Положив
. Положив  , а
, а 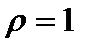 , мы получим единичную сферу в пространстве
, мы получим единичную сферу в пространстве  уравнение этой сферы имеет вид: ||x||1 = |x| + |y| и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае
уравнение этой сферы имеет вид: ||x||1 = |x| + |y| и такая метрика называется октаэдрической, потому что единичной сферой в трёхмерном случае 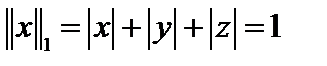 будет октаэдр.
будет октаэдр. уравнение этой сферы имеет вид: ||x||2 = (|x|2 + |y|2)1/2 – и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера.
уравнение этой сферы имеет вид: ||x||2 = (|x|2 + |y|2)1/2 – и такая метрика называется евклидовой (сферической), потому что единичной сферой в трёхмерном случае будет обычная сфера. будет куб.
будет куб.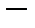 чебышёвская(кубическая) метрика; 2
чебышёвская(кубическая) метрика; 2  изображен пунктиром. При
изображен пунктиром. При 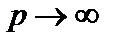 гёльдеровская группа метрик стремится к чебышевской.
гёльдеровская группа метрик стремится к чебышевской.
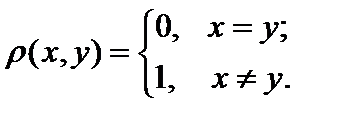 Здесь
Здесь 
 любое непустое множество.
любое непустое множество.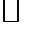 Первые две аксиомы очевидны. Проверим третью.
Первые две аксиомы очевидны. Проверим третью. Пусть неверно, что
Пусть неверно, что 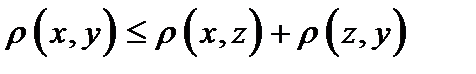 . Тогда
. Тогда  Но тогда
Но тогда 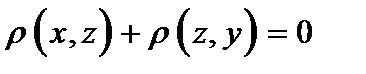 , то есть
, то есть 
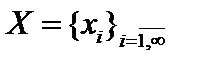 , с метрикой
, с метрикой 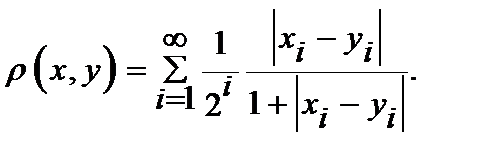
 .Так как
.Так как  , то
, то  , то есть
, то есть 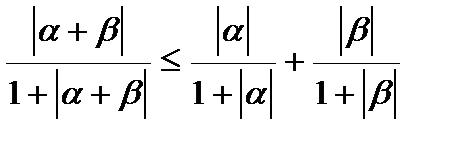 . Пусть
. Пусть 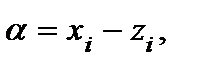
 , тогда
, тогда 
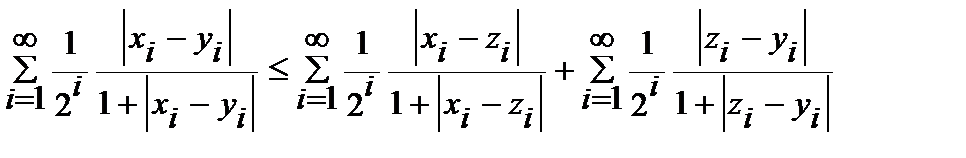 , или
, или 
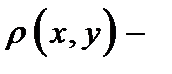 метрика на носителе
метрика на носителе 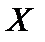 .Тогда
.Тогда 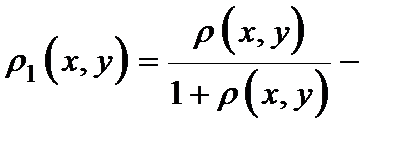 тоже метрика на носителе
тоже метрика на носителе 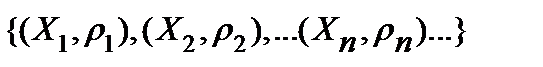
 последовательность метрических пространств. Прямым (декартовым) произведением этих метрических пространств называется пара
последовательность метрических пространств. Прямым (декартовым) произведением этих метрических пространств называется пара  , где
, где 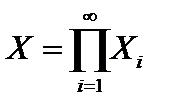 , а
, а 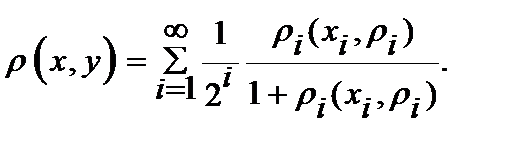
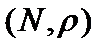
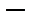 метрическое пространство, если метрика на носителе
метрическое пространство, если метрика на носителе 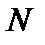 задана так:
задана так: 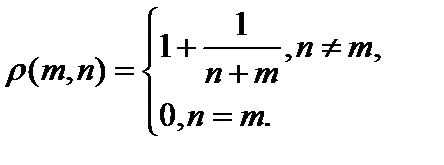
 Неравенство треугольника для несовпадающих точек
Неравенство треугольника для несовпадающих точек 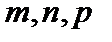 очевидно:
очевидно: 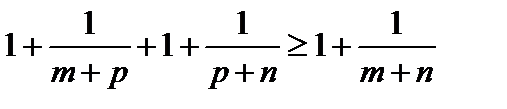 .
. 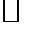 В этой метрике при
В этой метрике при 
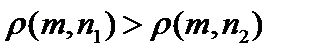 то есть натуральные числа чем дальше они расположены на числовой оси, тем ближе по метрике
то есть натуральные числа чем дальше они расположены на числовой оси, тем ближе по метрике 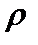 .
. ;
; ; в)
; в) 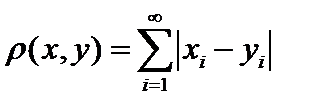 на множестве ограниченных последовательностей?
на множестве ограниченных последовательностей?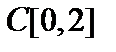 найти расстояние между функциями а)
найти расстояние между функциями а) 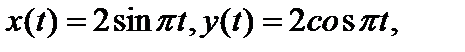 (
(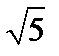 ); б)
); б) 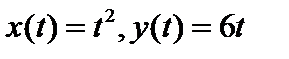 (8);
(8);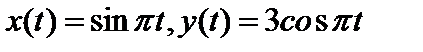 (5); г)
(5); г) 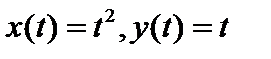 (
( ).
). найти расстояние между функциями
найти расстояние между функциями 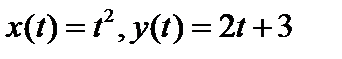 .
.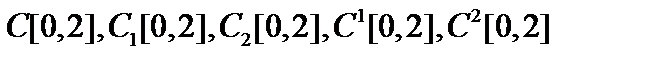 найти расстояние между функциями а)
найти расстояние между функциями а)  ; б)
; б) 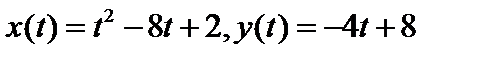 .
.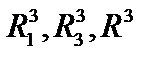 найти нормы элементов
найти нормы элементов 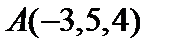 и
и 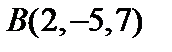 и расстояние между ними.
и расстояние между ними.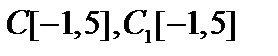 найти норму элемента
найти норму элемента 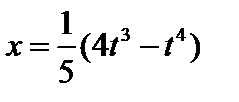 .
.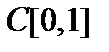 не гильбертово.
не гильбертово.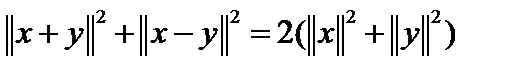 . Пусть
. Пусть 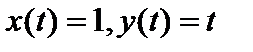 .Тогда, вычисляя норму в пространстве
.Тогда, вычисляя норму в пространстве 
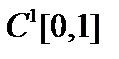 использовать норму пространства
использовать норму пространства 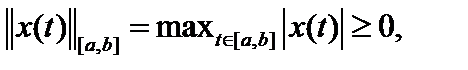 причём
причём 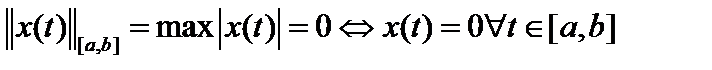 . 2.
. 2.  .
.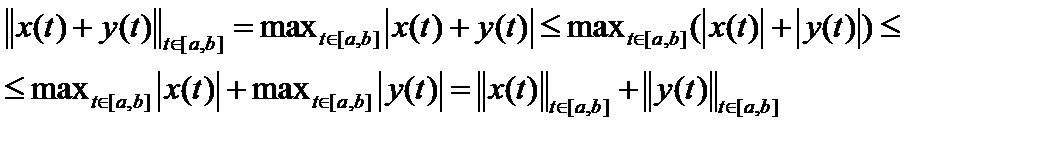
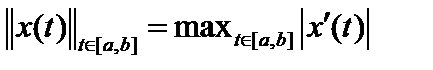 ?
? 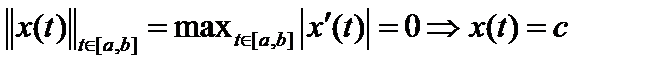 , где
, где 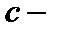 произвольная константа.
произвольная константа.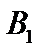 банахова пространства
банахова пространства 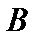 является банаховым пространством.
является банаховым пространством.
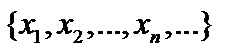 фундаментальна в подпространстве
фундаментальна в подпространстве 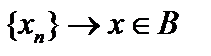 . Так как
. Так как 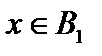 . Таким образом, произвольная фундаментальная последовательность в подпространстве
. Таким образом, произвольная фундаментальная последовательность в подпространстве  банахово по определению.
банахово по определению. 


