
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение метрического пространстваСодержание книги
Поиск на нашем сайте
Потребности науки и техники потребовали изучения значительно более общего понятия пространства по сравнению с эвклидовым пространством. Ниже мы рассмотрим основные понятия теории метрических пространств, то есть множеств, состоящих из элементов произвольной природы, на которое накладывается только одно требование: должно быть определено понятие расстояния между его элементами, удовлетворяющее некоторым условиям. Определение. Метрическим пространством называется всякое множество 1. 2. 3. для любых трех элементов Определение. Элементы Рассмотрим примеры. Пример 1. Множество действительных чисел с расстоянием
образует метрическое пространство Пример 2. Множество всевозможных наборов из
называется
Пример 3. Множество, точками которого является всевозможные последовательности
вещественных чисел, удовлетворяющие условию
а расстояние определяется равенством
является метрическим пространством, которое обозначают символом
Пример 4. Множество всех непрерывных действительных функций определенных на промежутке
т.е. в этом случае расстояние есть максимальное отклонение одной функции от другой. Это метрическое пространство обозначают символом Пример 5. Как и примере 4, рассмотрим множество всех функций непрерывных на
Такое метрическое пространство называют пространством непрерывных функций с квадратичной метрикой и обозначают символом
Пример 6. Если для множества функций, рассмотренных в примерах 4 и 5, определять расстояние с помощью равенства
то получим метрическое пространство, которое обозначают символом Из трех последних примеров следует, что метрические пространства, хотя и состоящие из одних и тех же элементов, но с различными определениями расстояний, следует считать различными.
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.005 с.) |

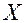 элементов произвольной природы вместе с однозначной, неотрицательной, действительной функцией
элементов произвольной природы вместе с однозначной, неотрицательной, действительной функцией 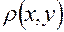 , определенной для любых элементов
, определенной для любых элементов  и
и  из
из  тогда и только тогда, когда
тогда и только тогда, когда  ;
; аксиома симметрии;
аксиома симметрии; выполняется неравенство
выполняется неравенство  аксиома треугольника.
аксиома треугольника. обозначают одной буквой
обозначают одной буквой 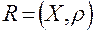 .
.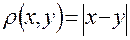
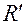 .
. упорядоченных чисел вида
упорядоченных чисел вида  ,
,  , принимаемых за точки
, принимаемых за точки  ,
,  расстояния между которыми определяется равенством
расстояния между которыми определяется равенством
 .
.
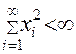 ,
, ,
, .
. , причем расстояние для любых двух элементов
, причем расстояние для любых двух элементов  и
и 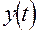 определено по формуле
определено по формуле ,
, .
. .
. .
. ,
,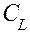 .
.


