
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Действия над линейными операторамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Над линейными операторами, определяемыми в линейном пространстве, можно производить различные действия, приводящие к новым линейным операторам. Рассмотрим здесь действия сложения операторов, умножения на число и умножения операторов друг на друга. 1. Сложения линейных операторов Пусть в пространстве Определение. Суммой операторов
где Можно показать, что сумма линейных операторов является линейным оператором, причем его матрица
Определение. Произведением линейного оператора
где
Можно показать, что оператор 3. Умножение линейных операторов Применим к произвольному вектору оператор
Определение. Оператор
при этом используется запись Можно показать, что произведение линейных операторов есть снова линейный оператор, а его матрица
4. Сопряженный оператор Определение. Оператор
Можно показать, что если оператор
является матрицей оператора
Такая матрица
Можно показать, что имеет место следующая теорема. Теорема (Альтернатива Фредгольма) Пусть
Тогда или уравнение
где
имеет, по крайней мере, одно ненулевое решение. Определение. Линейный оператор
Определение. Квадратная матрица
Можно показать, что матрица Глава 4. Преобразование координат
Замена базиса
Нетрудно заметить, что если в
Для каждого из ортов
где
Подставляя (4.3) в (4.2), получим
Сравнивая теперь (4.1) с (4.4) и учитывая единственность разложения вектора
Если ввести в рассмотрение одностолбцовые матрицы
и матрицу
то систему (4.5) можно заменить одним матричным равенством.
Матрицу
§ 2. Ортогональные преобразования
В евклидовом пространстве наибольший интерес представляет случай, когда каждый из базисов
Подставляя (4.3) в (4.7) и учитывая, что векторы
Определение. Всякая матрица Можно показать, что при ортогональном преобразовании сохраняются длины векторов и углы между ними. Докажем, что если матрица
Для доказательства вычислим произведение
Умножая обе части матричного равенства
Но так как
откуда следует
Таким образом, определитель ортогональной матрицы равен либо
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.146.237 (0.011 с.) |

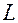 заданы линейные операторы
заданы линейные операторы  и
и  .
.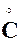 , для которого выполняется равенство
, для которого выполняется равенство ,
, – любой вектор из
– любой вектор из  равна сумме матриц
равна сумме матриц 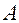 и
и  операторов
операторов  .
.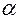 называется оператор
называется оператор  , определяемый равенством
, определяемый равенством ,
, .
.
 .
.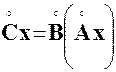 ,
,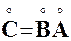 .
. .
. называется сопряженным по отношению к оператору
называется сопряженным по отношению к оператору  из пространства
из пространства  .
.
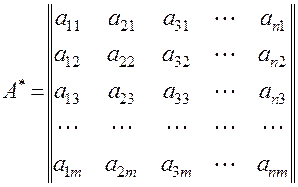 .
. называется сопряженной по отношению к матрице
называется сопряженной по отношению к матрице  . При этом, если оператор
. При этом, если оператор  .
. на евклидово пространство
на евклидово пространство  ,
,
 .
. ,
,  .
. -мерном пространстве имеется два базиса
-мерном пространстве имеется два базиса  и
и  , то координаты произвольного вектора в одном базисе будут отличаться от координат того же вектора в другом базисе. Выясним, как связаны координаты произвольного вектора
, то координаты произвольного вектора в одном базисе будут отличаться от координат того же вектора в другом базисе. Выясним, как связаны координаты произвольного вектора  и
и  координаты вектора
координаты вектора  относительно базисов
относительно базисов  и
и  соответственно, сможем написать
соответственно, сможем написать ; (4.1)
; (4.1)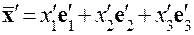 . (4.2)
. (4.2) ;
;  ; (4.3)
; (4.3) ,
,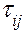
 – координаты вектора
– координаты вектора 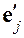 в базисе
в базисе 
 (4.4)
(4.4) (4.5)
(4.5) ,
, 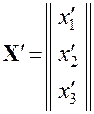
 ,
, . (4.6)
. (4.6) называют матрицей поворота координатной системы. Итак, координаты вектора
называют матрицей поворота координатной системы. Итак, координаты вектора  ,
, 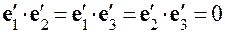 . (4.7)
. (4.7) ;
; 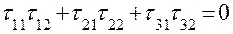 ;
; ;
;  ; (4.8)
; (4.8) ;
;  .
. и транспонированная
и транспонированная  совпадают, т.е.
совпадают, т.е.

 . (4.10)
. (4.10) справа на
справа на  .
. , а
, а  , то предыдущее равенство можно записать в виде
, то предыдущее равенство можно записать в виде ,
,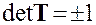 .
. , либо
, либо  .
.


