
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение линейного оператораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В общем курсе математического анализа изучаются функции одного или нескольких вещественных переменных. Например, в случае функции трех вещественных переменных можно говорить о функции, аргументом которой является свободный вектор трехмерного пространства. Ниже мы будем изучать функции, аргументом которых будет вектор произвольного линейного пространства. Причем мы рассмотрим простейшие типы таких функций, а именно линейные функции. При этом линейные числовые функции векторного аргумента, т.е. функции, значения которых суть числа называют линейными формами (функционалами), а линейные векторные функции векторного аргумента, значения которых суть векторы называют линейными операторами (отображениями, преобразованиями). Пусть заданы два различных непустых множества Определение 1. Правило (закон), по которому любому элементу Если оператор обозначить буквой
Множество Будем в дальнейшем под Определение 2. Оператор 1. 2. Покажем, что любой линейный оператор
Выпишем разложения векторов
где
Векторы
где
Используя единственность разложения вектора в данном базисе, приравняем коэффициенты при базисных векторах в левой и правой частях последнего равенства. При этом получим
Непосредственно из формулы (3.1) видно, что правило перехода от вектора
составленной из коэффициентов формул (3.1).
Определение. Матрица Если ввести в рассмотрение одностолбцовую матрицу
и вычислить произведение матриц
то получим одностолбцовую матрицу, элементами которой являются суммы, стоящие в правых частях равенств (3.1). Если же ввести в рассмотрение матрицу
и воспользоваться понятием равенства матриц, то система (3.1) может быть записана в виде
Примеры линейных операторов
Отметим матричную запись указанных выше свойств линейных операторов линейного пространства: 1. Образ суммы векторов равен сумме образов складываемых векторов. Если
2. Если
Наибольший интерес представляют такие операторы, при которых для каждого вектора (точки) существует единственный прообраз. Это значит, что уравнение (3.5) должно быть разрешено относительно
Если матрица Примеры линейных операторов Приведем наиболее известные примеры линейных операторов и соответствующие им матрицы. 1. Поворот плоскости Для вывода формул преобразования координат сделаем чертеж (рис.1).
Рис. 1
2. Обозначим через
Учитывая, что
получаем формулы преобразования координат
а тогда для матрицы оператора имеем
3. Растяжение вдоль оси 4.
а матрица оператора
Рис.2
5. Зеркальное отражение относительно оси
матрица оператора
а на чертеже (рис.2) произвольной точке
6. Поворот в обычном трехмерном пространстве
а матрица оператора
7. Тождественный оператор. Так называется оператор, при котором преобразование координат определяется формулами 8.
и, следовательно, матрица оператора в любом базисе имеет вид
9. Нулевой оператор. Для всех векторов
Матрица этого оператора обозначается
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

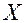 и
и 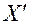 , элементы которых будем обозначать буквами соответственно
, элементы которых будем обозначать буквами соответственно  и
и  .
. ставится в соответствие единственный элемент
ставится в соответствие единственный элемент  называется оператором, действующим из
называется оператором, действующим из  , то результат
, то результат  .
. , называются ядром оператора
, называются ядром оператора 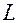 .
. из
из 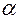 выполняются условия:
выполняются условия: (аддитивность);
(аддитивность); (однородность).
(однородность). и обозначим через
и обозначим через  .
.
 ,
, и
и  координаты векторов соответственно
координаты векторов соответственно  и
и  .
. принадлежат пространству
принадлежат пространству 

 – координаты вектора
– координаты вектора  в базисе
в базисе 
 .
. (3.1)
(3.1) к вектору
к вектору  или от точки
или от точки  к новой точке
к новой точке  * полностью определяется квадратной матрицей
* полностью определяется квадратной матрицей , (3.2)
, (3.2) называется матрицей линейного оператора
называется матрицей линейного оператора 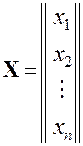 (3.3)
(3.3) ,
, (3.4)
(3.4) . (3.5)
. (3.5) и
и  – одностолбцовые матрицы, соответствующие складываемым векторам, то
– одностолбцовые матрицы, соответствующие складываемым векторам, то .
. – произвольное число, а
– произвольное число, а  – одностолбцовая матрица, соответствующая данному вектору, то
– одностолбцовая матрица, соответствующая данному вектору, то .
. . Ранее было показано, что это возможно только в том случае, если матрица
. Ранее было показано, что это возможно только в том случае, если матрица  неособенная. В этом случае можем написать
неособенная. В этом случае можем написать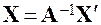 .
. вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки, так что произвольный вектор
против часовой стрелки, так что произвольный вектор  переходит в вектор
переходит в вектор  .
.
 и
и 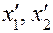 соответственно координаты векторов
соответственно координаты векторов  ;
; .
. и
и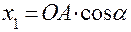 ;
;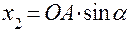 ,
, ;
; ,
, .
. в
в  раз, а вдоль оси
раз, а вдоль оси  , в
, в  раз. Формулы преобразования координат в этом случае имеют вид:
раз. Формулы преобразования координат в этом случае имеют вид:
 .
.

 ,
, будет соответствовать точка
будет соответствовать точка  .
. на угол
на угол 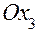 . Формулы преобразования координат имеют в этом случае следующий вид
. Формулы преобразования координат имеют в этом случае следующий вид
 .
.
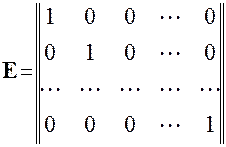 .
. из
из  имеем
имеем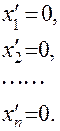
 и состоит из одних нулей, так что
и состоит из одних нулей, так что .
.


