
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Малые колебания механических системСодержание книги
Поиск на нашем сайте
Из курса «Теоретическая механика» известно, что положение механической системы с В случае голономных связей уравнения Лагранжа второго рода имеют вид:
где
коэффициенты которой зависят от координат Для консервативных действующих сил элементарная работа равна уменьшению потенциальной энергии
Пусть точка
то есть положения равновесия системы возможны только в стационарных точках потенциальной энергии. Можно показать, что точка минимума потенциальной энергии отвечает устойчивому положению равновесия. Рассмотрим такую точку. Без ограничения общности можно считать, что в этой точке
Так как обе квадратичные формы
приводящие квадратичные формы
В обобщенных координатах
решения которых могут быть записаны в виде
где константы
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.158 (0.008 с.) |

 степенями свободы задается с помощью
степенями свободы задается с помощью  .
.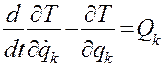 ,
,  , (7.23)
, (7.23) – обобщенные силы, а
– обобщенные силы, а  – кинетическая энергия системы, равная половине суммы произведений масс точек системы на квадрат их скоростей, то есть выражается в виде некоторой квадратичной формы относительно обобщенных скоростей
– кинетическая энергия системы, равная половине суммы произведений масс точек системы на квадрат их скоростей, то есть выражается в виде некоторой квадратичной формы относительно обобщенных скоростей 
 , (7.24)
, (7.24) , которую также можно считать выраженной через обобщенные координаты, при этом
, которую также можно считать выраженной через обобщенные координаты, при этом ,
,  означает состояние равновесия рассматриваемой системы. В состоянии равновесия
означает состояние равновесия рассматриваемой системы. В состоянии равновесия  , а тогда кинетическая энергия системы равна нулю и все ее частные производные по
, а тогда кинетическая энергия системы равна нулю и все ее частные производные по 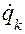 также равна нулю, ибо они представляют собой линейные формы от
также равна нулю, ибо они представляют собой линейные формы от  ,
,  и само значение потенциальной энергии также равно нулю. Если ограничиться изучением движения системы в малой окрестности нулевой точки, то коэффициенты квадратичной формы
и само значение потенциальной энергии также равно нулю. Если ограничиться изучением движения системы в малой окрестности нулевой точки, то коэффициенты квадратичной формы  .
.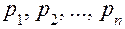
 ,
,  ,
, 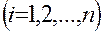 ,
, ,
, .
. ,
,  ,
,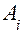 и
и  определяются из начальных условий. Величины
определяются из начальных условий. Величины 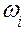 называются собственными частотами системы. Следовательно, каждая из координат
называются собственными частотами системы. Следовательно, каждая из координат  совершает гармонические колебания с собственной частотой
совершает гармонические колебания с собственной частотой 


