
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходимость. Полные метрические пространстваСодержание книги
Поиск на нашем сайте
Введем некоторые понятия теории метрических пространств, которые будут использованы в дальнейшем. Пусть Определение. Совокупность точек
называется замкнутым шаром и обозначается символом Точка Определение. Совокупность точек
называется открытым шаром и обозначается символом Открытый шар радиуса Определение. Точка Совокупность всех точек прикосновения множества Определение. Точка Определение. Точка Пусть Определение. Последовательность
Следующая теорема устанавливает связь между понятиями предела и точкой прикосновения множества. Теорема. Для того чтобы точка Пусть в метрическом пространстве Определение. Множество Например, множество рациональных чисел всюду плотно на числовой прямой. Пространства, в которых имеется счетные всюду плотные множества, называют сепарательными. Определение. Множество Определение. Последовательность Нетрудно заметить, что всякая сходящаяся последовательность является фундаментальной. Однако обратное утверждение верно не во всяком метрическом пространстве. Определение. Если в метрическом пространстве Например, евклидовы пространства
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

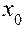 означает некоторую точку метрического пространства
означает некоторую точку метрического пространства  , а
, а 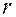 – положительное число.
– положительное число. пространства
пространства 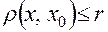
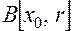 .
.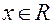 , удовлетворяющих неравенству
, удовлетворяющих неравенству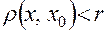 ,
,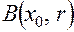 .
.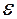 с центром в точке
с центром в точке 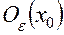 .
.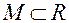 , если любая ее окрестность содержит хотя бы одну точку из
, если любая ее окрестность содержит хотя бы одну точку из 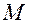 .
.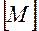 .
.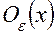 нет точек из
нет точек из 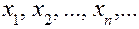 – последовательность точек в метрическом пространстве
– последовательность точек в метрическом пространстве 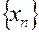 сходится к точке
сходится к точке 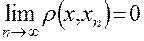 .
. и
и 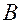 .
.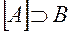 . В частности, множество
. В частности, множество 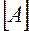 совпадает со всем пространством
совпадает со всем пространством 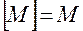 .
.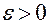 существует такое число
существует такое число 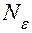 , что для всех
, что для всех 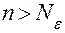 и
и 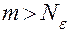 выполняется неравенство
выполняется неравенство 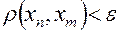 .
.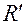 ,
, 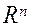 , а также пространство
, а также пространство 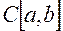 являются полными.
являются полными.


