
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип сжимающих отображенийСодержание книги
Поиск на нашем сайте
Вопрос о существовании и единственности решений алгебраических, трансцендентных, дифференциальных и других типов уравнений можно сформулировать в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Одним из критериев существования и единственности неподвижной точки при такого рода отображениях является так называемый принцип сжимающих отображений. Отображение
Точка
Можно показать, что имеет место следующее утверждение. Теорема (Принцип сжимающих отображений). Всякое сжимающее отображение, определенное в полном метрическом пространстве Принцип сжимающих отображений можно использовать для доказательства существования и единственности решений для уравнений различных типов. Следует отметить, что принцип сжимающих отображений позволяет не только доказать существование и единственность решения, но и дает метод нахождения приближенного решения. Этот метод называют методом итераций или методом последовательных приближений. Рассмотрим применение этого метода к отысканию приближенного решения уравнения
где функция
с константой В этом случае
сходится к единственному корню уравнения (8.1). Если функция
где
Рассмотрим примеры. Пример 1. На промежутке
Записав данное уравнение в виде (8.1), получим
Легко проверяется, что производная Используя метод итераций и положив в первом шаге
Пример 2. На промежутке
Как и в предыдущем примере запишем данное уравнение в виде
В этом примере производная
Геометрически метод итераций можно пояснить следующим образом. Построим на плоскости
Рис.3
Отправляясь от некоторой точки Возможен также (рис.4) другой вид ломаной
Рис.4 Если
Рис. 5
Пусть теперь требуется решить уравнение
где
где Так как
Выберем теперь число
Решая систему (8.5) двух уравнений относительно
и заметим, что условие Пример. Требуется найти приближенное значение корня уравнения
на промежутке Легко проверяется, что
а тогда в соответствии с равенствами (8.6), получим
Введем в рассмотрение функцию
и используя метод итераций положим сначала
То есть для получения искомого решения проделали 12 шагов.
Библиографический список
1. Вулих Б.З. Введение в функциональный анализ. ГИФМЛ, М, 1958. 2. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Изд-во «Наука». Гл. ред. физ-мат. лит. М. – 1972. 3. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений. Гос. Изд-во физ-мат. лит. М, 1962. 4. Треногин В.А. Функциональный анализ. Изд-во «Наука». Гл. ред. физ-мат. лит. М. – 1980. 5. Шилов Г.Е. Введение в теорию линейных пространств. Гос. Изд-во техн-теор. лит. М, 1956. Предметный указатель
оглавление Предисловие. 3 Введение. 4 Глава 1. Линейные пространства. 5 § 1. Введение. 5 § 2. Определение линейного пространства. 7 § 3. Свойства линейного пространства. 9 § 4. Линейная зависимость. 12 § 5. Базис и координаты.. 14 § 6. Размерность. 16 § 7. Подпространства. 16 Глава 2. Евклидовы пространства. 19 § 1. Введение. 19 § 2. Определение евклидова пространства. 20 § 3. Длина вектора. 22 § 4. Неравенство Коши-Буняковского. 23 § 5. Неравенство треугольника. 24 § 6. Угол между векторами. 25 § 7. Ортонормированный базис. 26 Глава 3. Линейные операторы.. 29 § 1. Определение линейного оператора. 29 § 2. Примеры линейных операторов. 33 § 3. Действия над линейными операторами. 39 Глава 4. Преобразование координат. 43 § 1. Замена базиса. 43 § 2. Ортогональные преобразования. 46 § 3. Матрица оператора при замене базиса. 48 Глава 5. Несовместные системы линейных уравнений и метод наименьших квадратов. 49 § 1. Задача о проекции вектора и перпендикуляре к нему. 49 § 2. Несовместные системы линейных уравнений. 50 § 3. Метод наименьших квадратов. 54 Глава 6. Собственные векторы и собственные числа. 57 § 1. Определение собственных векторов и собственных чисел. 57 § 2. Вычисление собственных векторов и собственных чисел в конечномерном пространстве. 58 § 3. Собственные векторы симметричных операторов. 62 Глава 7. Квадратичные формы и их приведение к каноническому виду. 64 § 1. Приведение квадратичной формы к каноническому виду. 64 § 2. Приведение двух квадратичных форм к каноническому виду. 73 § 3. Малые колебания механических систем.. 78 Глава 8. Элементы теории метрических пространств. 82 § 1. Определение метрического пространства. 82 § 2. Сходимость. Полные метрические пространства. 84 § 3. Принцип сжимающих отображений. 87 Библиографический список. 95 Предметный указатель. 96
Ольга Владимировна Афанасьева Александр Алексеевич Потапенко
Функциональный анализ В задачах управления Учебное пособие
Редактор И.Н. Садчикова
Сводный темплан 2005 г.
Лицензия ЛР № 020308 от 14.02.97
Санитарно-эпидемиологическое заключение № 78.01.07.953.П.005641.11.03. от 24.11.2003 г.
Подписано в печать Формат 60´84 1/16
Б.кн.-журн. П.л. Б.л. РТП РИО СЗТУ
Тираж 100 Заказ
Северо-Западный государственный заочный технический университет РИО СЗТУ, член Издательско-полиграфической ассоциации университетов России 191186, Санкт-Петербург, ул. Миллионная, 5 * Иногда апеллируя к привычным геометрическим представлениям, элементы линейного пространства называют не векторами, а точками; естественно, такое изменение названия не влечет никаких изменений в содержании изложенного.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.105.85 (0.009 с.) |

 метрического пространства
метрического пространства  в себя называется сжимающим отображением, если существует такое число
в себя называется сжимающим отображением, если существует такое число 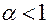 , что для любых двух точек
, что для любых двух точек  и
и  пространства
пространства  .
. .
.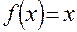 , (8.1)
, (8.1) определена на промежутке
определена на промежутке  и удовлетворяет условию Липшица
и удовлетворяет условию Липшица , (8.2)
, (8.2)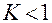 и отображает промежуток
и отображает промежуток  есть сжимающее отображение и, согласно сформулированной выше теореме последовательность чисел
есть сжимающее отображение и, согласно сформулированной выше теореме последовательность чисел ,
,  ,
,  ,…,
,…, 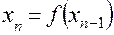 …
… и при этом выполняется неравенство
и при этом выполняется неравенство , (8.3)
, (8.3) – некоторая постоянная, то легко видеть, что условие сжатости (8.2) выполнено.
– некоторая постоянная, то легко видеть, что условие сжатости (8.2) выполнено.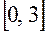 найти действительный корень уравнения
найти действительный корень уравнения .
. .
. на промежутке
на промежутке  , получим с помощью Mathcad Professional,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
, получим с помощью Mathcad Professional,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
 .
. .
. на промежутке
на промежутке 
 графики функций
графики функций  и
и  . Каждый вещественный корень
. Каждый вещественный корень  уравнения (8.1) является абсциссой точки пересечения кривой
уравнения (8.1) является абсциссой точки пересечения кривой 
 , построим ломаную линию
, построим ломаную линию  («Лестница»), звенья которой попеременно параллельны оси
(«Лестница»), звенья которой попеременно параллельны оси  и оси
и оси  , так что вершины
, так что вершины  лежат на кривой
лежат на кривой  на прямой
на прямой  и
и  ,
, 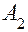 и
и  ,
,  и
и  … представляют собой последовательные приближения
… представляют собой последовательные приближения  к корню
к корню  («Спираль»). Легко заметить, что решение в виде «лестницы» получается, если производная
(«Спираль»). Легко заметить, что решение в виде «лестницы» получается, если производная 
 , то процесс итерации может быть расходящимся (рис.5).
, то процесс итерации может быть расходящимся (рис.5).
 , причем примем для определенности, что
, причем примем для определенности, что  ,
,  и на
и на 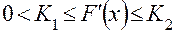 , (8.4)
, (8.4) и
и  – некоторые постоянные. Введем в рассмотрение функцию
– некоторые постоянные. Введем в рассмотрение функцию ,
, – некоторая постоянная и заметим, что решение уравнения
– некоторая постоянная и заметим, что решение уравнения 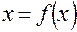 равносильно решению уравнения
равносильно решению уравнения  , то, используя (8.4) будем иметь
, то, используя (8.4) будем иметь .
. ,
,  (8.5)
(8.5) ,
, 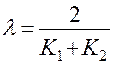 (8.6)
(8.6)
 , а
, а  . Выпишем производную
. Выпишем производную  и заметим, что на промежутке
и заметим, что на промежутке  ,
, ,
,  .
.




