Точность работы при случайных воздействиях
Похожие статьи вашей тематики
| Точность работы линейной САУ при стационарных случайных воздействиях
|  
|  
|  
| Для оценки качества (точности) системы при случайных воздействиях используются следующие характеристики случайного процесса: mε,σε, Dε. Среднее значение (математическое ожидание) mε называется систематической ошибкой. При вычислении систематической ошибки в установившемся режиме, как и в детерминированном случае, можно использовать коэффициенты ошибок, т.е.
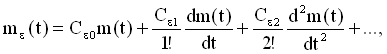 (9.18) (9.18)
где 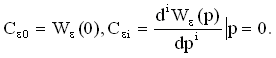
Дисперсия ошибки может быть определена по корреляционной функции и функции спектральной плотности
 (9.19) (9.19)
т.е. дисперсия ошибки пропорциональна площади между кривой спектральной плотности ошибки и осью абсцисс. Спектральная плотность может быть задана аналитически или в виде графиков, поэтому и существуют аналитические и графоаналитические методы исследования САУ со случайным сигналом.
Графоаналитический метод применяется тогда, когда САУ описывается уравнением высокого порядка и спектральная плотность описывается сложным уравнением или представлена в виде экспериментально полученного графика. Он является наглядным и позволяет решить, как нужно изменить частотные характеристики, чтобы уменьшить дисперсию ошибки.
Порядок расчета следующий:
1. строится АЧХ |Wε(jω)| замкнутой САУ по ошибке. Ординаты этой кривой возводятся в квадрат и строится кривая |Wε(jω)|2 (рис.9.3);
2. строится кривая спектрально плотности ошибки Sε(ω)=|Wε(jω)2| Sf(ω), где Sf(ω) - спектральная плотность на входе;
3. определяется значение интеграла 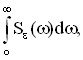 для чего подсчитывается площадь, заключенная между Sε(ω) и осью абсцисс; для чего подсчитывается площадь, заключенная между Sε(ω) и осью абсцисс;
4. среднеквадратическая ошибка или дисперсия определяется по формуле
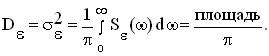

Рис.9.3. Диаграмма спектральной плотности ошибки
Как видно из графиков для Sε(ω) ошибка зависит от взаимного расположения графиков |Wε(jω)| и Sf(ω). При совпадении максимумов характеристик ошибка оказывается большой. Для ее снижения необходимо разносить максимумы |Wε(jω)| и Sf(ω).
При использовании аналитических методов расчета дисперсии ошибки спектральная плотность ошибки представляется в виде дробно-рациональной функции 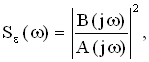 где А(jω) и B(jω) - полиномы, зависящие от АЧХ САУ и спектральной плотности возмущающего воздействия. Тогда для вычисления интеграла где А(jω) и B(jω) - полиномы, зависящие от АЧХ САУ и спектральной плотности возмущающего воздействия. Тогда для вычисления интеграла
 (9.20) (9.20)
можно использовать рекуррентные формулы, приведенные в справочной литературе [2].
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного
| Точность работы нелинейной САУ при стационарных случайных воздействиях
|  
|  
|  
| В большинстве задач исследования точности работы САУ со случайным сигналом нелинейные системы можно представить совокупностью линейных инерционных и нелинейных безынерционных элементов, характеристики которых не имеют в каждой точке производных и не могут быть разложены в ряд Тейлора. Тогда зависимость между входом и выходом таких НЭ приближенно представляется в виде кусочно-линейной функции. В общем случае НЭ вызывают искажение входного сигнала, изменяют вид его закона распределения, существенно меняются динамические качества вплоть до возможной потери устойчивости и полного нарушения нормального режима работы.
Для нелинейных систем принцип суперпозиции не применим, поэтому невозможно для нелинейных систем в отличие от линейных отдельно рассматривать прохождение математического ожидания и дисперсии случайного процесса. Общих точных методов решения подобных задач не существует.
Наиболее эффективным приближенным методом исследования нелинейных САУ со случайным сигналом является метод статистической линеаризации [19], который применим и для случаев, когда нелинейные характеристики описываются недифференцируемыми функциями. Метод разработан и опубликован одновременно в 1954 г. И.Е.Казаковым (СССР) и В.Бутоном (США). Суть метода состоит в приближенной замене нелинейностей их линейными в статистическом смысле зависимостями, что позволяет при расчете замкнутых систем использовать хорошо разработанные методы линейных САУ. В качестве критерия эквивалентности такой замены принята минимизация разности процессов в нелинейной и линеаризованной системах.
Расчетная схема в этом случае приводится к виду рис.9.5.

Рис.9.5. Структурная схема нелинейной САУ при случайном воздействии
Метод статистической линеаризации применим при условии, что случайный сигнал является стационарным с нормальным законом распределения. Заметим, что закон распределения тем ближе к нормальному, чем инерционнее, т.е. более узкополосна линейная система. Входной сигнал в системе рис.9.5 может представлять собой либо полезный сигнал, либо линейную комбинацию помех и полезного сигнала.
Статистически линеаризованная система представляется в виде двух линейных систем и будет иметь различные передаточные функции для математического ожидания mg и для центрированной составляющей ошибки x0.
Пользуясь известными свойствами передаточной функции, получим следующие передаточные функции ошибки рассматриваемой линеаризованной системы:
по математическому ожиданию (полезному сигналу)
 ; (9.21) ; (9.21)
по центрированной составляющей (помехе)
 , (9.22) , (9.22)
где Ко(mx,Dx) и К1(mx,Dx) - коэффициенты статистической линеаризации, зависящие от математического ожидания и дисперсии на входе нелинейного элемента НЭ. Они определяются по формулам или графикам, приведенным в справочной литературе [2,19] в виде функций пока неизвестных величин mx и Dx.
Эти передаточные функции взаимосвязаны через Ко(mx,Dx) и К1(mx,Dx), поэтому необходимо совместное решение двух уравнений. Из передаточных функций находятся (см. линейную ТАУ):
 ; (9.23) ; (9.23)
 . (9.24) . (9.24)
Совместное решение уравнений (9.23) и (9.24) можно производить либо методом последовательных приближений, либо графоаналитическим. Если в САУ имеются два нелинейных элемента, разделенных инерционным звеном, то для определения параметров каждого НЭ приходится решать систему из четырех уравнений. Это, естественно, усложняет расчеты.
При решении задачи методом последовательных приближений задаются некоторыми значениями коэффициентов Ко и К1 и по формулам (9.23) и (9.24) определяют mx и Dx в первом приближении. По найденным значениям mx и Dx уточняют величины Ко и К1. Затем вновь определяют mx и Dx во втором приближении и т.д. Расчет заканчивается при требуемой точности совпадения принятых и расчетных mx и Dx.
Графоаналитическое решение уравнений (9.23) и (9.24) сводится к построению в координатах mx, Dx кривых, соответствующих этим двум уравнениям, и в определении точки их пересечения.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и
Статистический синтез САУ является достаточно сложной задачей. Построение САУ, имеющей минимум средних потерь, означает ограничение в определенной степени дисперсии случайных помех и обеспечение требуемой точности воспроизведения задающего воздействия. Как указывалось ранее, эти два требования противоречивы: уменьшение дисперсии случайных помех обычно приводит к снижению динамической точности, и наоборот.
При выборе критерия оптимальности системы следует иметь в виду, что чем более полно критерий отражает назначение системы, тем он сложнее и тем труднее определять систему по такому критерию. Метод определения оптимальной системы и сама система зависят от исходных данных, характеризующих условия применения системы, например от вероятностных характеристик сигнала и помех, а также от класса систем, из которых она выбирается. Чаще всего для оценки оптимальности САУ используется критерий минимума среднеквадратической ошибки (СКО).
При синтезе САУ возможны два подхода:
1. синтез САУ при заданной структуре, когда по известным статистическим характеристикам входа и выхода подбираются ее параметры;
2. синтез САУ при произвольной структуре, когда по известным статистическим характеристикам входа и выхода определяют структуру и параметры системы, удовлетворяющих принятому критерию оптимальности.
Задача синтеза САУ по условию обеспечения требуемой точности сводится к определению передаточной функции системы, при которой выполняется неравенство
 , (9.25) , (9.25)
где Dε доп - допустимое значение дисперсии ошибки регулирования.
В соответствии с уравнением (9.25) спектральная плотность ошибки Sε(ω) зависит от вида передаточной функции системы и спектральной плотности воздействия. При исследовании САУ со случайным сигналом целесообразно на вход подавать типовое воздействие в виде "белого шума", для которого характерно: Rx(τ)=0 при τ  0 и S(ω)= const. В этом случае для вычисления интеграла от спектральной плотности ошибки (9.25) возможно использование аналитического метода [2,19]. А если спектральная плотность входного воздействия задана графически, то целесообразно использование для анализа и синтеза графоаналитического метода. Он наглядно показывает, что ошибка регулирования зависит от взаимного расположения графиков спектральной плотности воздействия и а.ч.х. передаточной функции ошибки САУ. Ранее было показано, что для снижения дисперсии ошибки необходимо разносить их максимумы, снижать пик а.ч.х., т.е. получать систему более узкополосной и достаточно задемпфированной. 0 и S(ω)= const. В этом случае для вычисления интеграла от спектральной плотности ошибки (9.25) возможно использование аналитического метода [2,19]. А если спектральная плотность входного воздействия задана графически, то целесообразно использование для анализа и синтеза графоаналитического метода. Он наглядно показывает, что ошибка регулирования зависит от взаимного расположения графиков спектральной плотности воздействия и а.ч.х. передаточной функции ошибки САУ. Ранее было показано, что для снижения дисперсии ошибки необходимо разносить их максимумы, снижать пик а.ч.х., т.е. получать систему более узкополосной и достаточно задемпфированной.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
П р и м е р. Пусть передаточная функция разомкнутой системы W(p)=k/(p(Tp+1)). На САУ подается полезный сигнал g(t)=g1t и помеха "белый шум" со спектральной плотностью Sf(ω)=N. Определить систематическую ошибку mε и среднеквадратическую ошибку σ. Структурная схема представлена на рис.9.4.
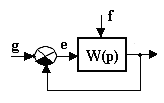
Рис.9.4. САУ со случайным сигналом
Р е ш е н и е. Систематическая ошибка определяется с применением коэффициентов ошибок

Тогда mε=0*g1t + g1(1/k)=g1/k.Дисперсия ошибки по формуле (9.20)
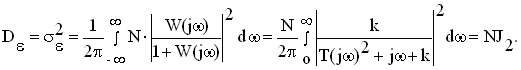
Для системы второго порядка величина интеграла J2 вычисляется по формуле [2,19]
 где где 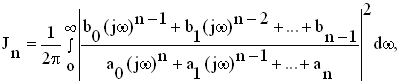
т.е. bo=0; a2=k; b1=k; a0=T; a1=1. Очевидно Dε=Nk/2 или 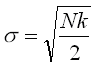 . .
Из полученных результатов следует, что увеличение общего коэффициента передачи разомкнутой цепи системы k с одной стороны ведет к уменьшению установившегося значения систематической ошибки системы mε. В тоже время, для уменьшения дисперсии ошибки, вызванной помехой на входе, необходимо, чтобы значение общего коэффициента передачи разомкнутой цепи системы k было минимально.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и
1. Дайте определение статистической динамики систем управления.
2. Изобразите базовую структуру модели системы при случайных воздействиях.
3. Перечислите и определите статистические характеристики случайных процессов.
4. Каково свойство эргодической гипотезы?
5. Поясните физический смысл корреляционной функции и спектральной плотности случайного процесса.
6. Каким образом производится оценка работы линейных систем при случайных стационарных сигналах?
7. Как определяется спектральная плотность выходной величины и ошибки системы?
8. Дайте определение средней квадратической ошибки системы и укажите способы ее вычислений.
9. Дайте определение "белого шума".
10. Приведите расчетную схему для исследования нелинейной САУ со случайным сигналом.
11. От каких параметров зависят коэффициенты статистической линеаризации нелинейностей?
12. Перечислите методы синтеза нелинейных САУ со случайным сигналом.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочн
Тема №10: Оптимальные САУ
Автоматические системы, обеспечивающие наилучшие технические или технико-экономические показатели качества при заданных реальных условиях работы и ограничениях, называются оптимальными системами.
Оптимальные системы делятся на два класса:
- системы с "жесткой" настройкой, в которых неполнота информации не мешает достижению цели управления;
- адаптивные системы, в которых неполнота информации не позволяет достичь цели управления без автоматического приспособления системы в условиях неопределенности.
Цель оптимизации - математически выражается как требование обеспечения минимума или максимума некоторого показателя качества, называемого критерием оптимальности или целевой функцией. Основными критериями качества автоматических систем являются: стоимость разработки, изготовления и эксплуатации системы; качество функционирования (точность и быстродействие); надежность; потребляемая энергия; масса; объем и т.д.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обуч
Качество функционирования описывается функциональными зависимостями вида:
 , ,
где u - координаты управления; x - фазовые координаты; fв - возмущения; tо и tк - начало и конец процесса.
При разработке оптимальных САУ необходимо учитывать ограничения, накладываемые на систему, которые бывают двух типов:
- естественные, обусловленные принципом работы объекта, например, скорость работы гидравлического сервомотора не может быть больше, чем при полностью открытых заслонках, скорость АД не может быть больше синхронной и т.д.;
- искусственные (условные), которые вводят сознательно, например, ограничения тока в ДПТ для нормальной коммутации, нагрева, ускорения для нормального самочувствия в лифте и т.д.
Критерии оптимальности могут быть скалярными, если представляются только одним частным критерием, и векторными (многокритериальными), если представляются рядом частных.
В качестве критерия оптимальности может быть принято время переходного процесса  т.е. САУ оптимальная по быстродействию, если обеспечивается минимум этого интеграла с учетом ограничений. Принимаются также известные в ТАУ интегральные оценки качества переходного процесса, например, квадратичный. В качестве критерия оптимальности систем при случайных воздействиях используют среднее значение квадрата ошибки системы т.е. САУ оптимальная по быстродействию, если обеспечивается минимум этого интеграла с учетом ограничений. Принимаются также известные в ТАУ интегральные оценки качества переходного процесса, например, квадратичный. В качестве критерия оптимальности систем при случайных воздействиях используют среднее значение квадрата ошибки системы  При управлении от источников с ограниченной мощностью берут функционал, характеризующий расход энергии на управление При управлении от источников с ограниченной мощностью берут функционал, характеризующий расход энергии на управление  где u(t) и i(t) - напряжение и ток цепи управления. Иногда в качестве критерия оптимальности сложных САУ принимают максимум прибыли технологического процесса I= где u(t) и i(t) - напряжение и ток цепи управления. Иногда в качестве критерия оптимальности сложных САУ принимают максимум прибыли технологического процесса I= 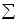 giПi - S, где gi - цена продукта; Пi - производительность; S - затраты. giПi - S, где gi - цена продукта; Пi - производительность; S - затраты.
По сравнению с менее строгими методами проектирования замкнутых САУ преимущества теории оптимизации состоят в следующем:
1). процедура проектирования является более четкой, т.к. включает в едином показателе проектирования все существенные аспекты качества;
2). очевидно проектировщик может ожидать получения наилучшего результата в соответствии с данным показателем качества. Поэтому для рассматриваемой задачи указывается область ограничений;
3). можно обнаружить несовместимость ряда требований качества;
4). процедура непосредственно включает в себя предсказание, т.к. оценка показателя качества производится по будущим значениям времени управления;
5). результирующая система управления будет адаптивной, если в процессе работы показатель проектирования переформулируется и попутно снова вычисляются параметры регулятора;
6). определение оптимальных нестационарных процессов не вносит каких-либо дополнительных трудностей;
7). непосредственно рассматриваются и нелинейные объекты, правда, при этом возрастает сложность вычислений.
Трудности, присущие теории оптимизации, состоят в следующем:
1). превращение различных требований проектирования в значимый на языке математики показатель качества непростая задача; здесь возможны пробы и ошибки;
2). существующие алгоритмы оптимального управления в случае нелинейных систем требуют сложных программ вычислений и, в ряде случаев, большого количества машинного времени;
3). показатель качества результирующей системы управления очень чувствителен к разного рода ошибочным предположениям и к изменениям параметров объекта управления.
Задача оптимизации решается в три этапа:
1). построение математических моделей физического процесса, а также требований качества. Математическая модель требований качества является показателем качества системы;
2). вычисление оптимальных управляющих воздействий;
3). синтез регулятора, формирующего оптимальные сигналы управления.
На рис.10.1 представлена классификация оптимальных систем.

Рис.10.1. Классификация оптимальных САУ
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного об
Если объект регулирования обладает характеристикой с экстремумом, то расчет такой системы заключается в определении частоты, амплитуды колебаний и величины потери поиска ("рыскания").
Экстремальные системы целесообразно применять в следующих случаях:
1. если существует показатель качества, с изменением которого происходит достаточно ощутимое изменение технико-экономической эффективности;
2. когда выгоды от увеличения технико-экономической эффективности существенно компенсируют затраты, обусловленные применением принципа экстремального управления;
3. если существуют возможности определения экстремума функционала качества и воздействия на регулирующие органы объекта с целью по лучения экстремального режима его работы.
Экстремальное управление применяют также в сложных системах комплексной автоматизации. При этом ставится задача определения оптимальных настроек локальных регуляторов автоматических систем из условия экстремума некоторого показателя качества в статических или установившихся режимах при различных возмущениях, нарушающих экстремальный режим.
Системы экстремального регулирования (СЭР) подразделяются на системы с запоминанием экстремума и системы, работающие по чувствительности. СЭР с запоминанием экстремума более простые и надежные, чем СЭР, работающие по чувствительности (например синхронного детектирования), но в случае многопараметрической системы существенно уступают последним в скорости выхода в зону экстремума. При дрейфе статических характеристик следует применять СЭР с коммутатором (возвратом). В этом случае экстремум не потеряется и исполнительный механизм не достигнет своего крайнего положения. Для улучшения работы СЭР с инерционными объектами следует применять динамическую оптимизацию, заключающуюся в измерении знака второй производной функции для изменения направления движения исполнительного механизма. В этом случае возможно снижение потерь поиска и уменьшение амплитуды колебаний в зоне экстремума.
СЭР подразделяются на системы, использующие поисковые сигналы и беспоисковые. Большое значение имеют беспоисковые экстремальные САУ (когда в системе не допускается наличие поисковых колебаний). Они затрачивают меньше времени на поиск, нет потерь энергии на управление и т.д. Это обеспечивается заменой поиска экстремума соответствующими обратными связями:
-по косвенному параметру;
-по сигналам моделей;
-в результате расчета управлений алгоритмическими методами;
-применением адаптивной модели.
Организация движения системы к экстремуму основана на использовании сигналов, зависящих от градиента функции, или сигналов отклонений от экстремума. Способы движения к экстремуму разделяются на: использующие случайный сигнал (случайный поиск) и регулярные. Из регулярных способов (методов) наибольшее применение нашли: Гаусса-Зейделя (или поочередного изменения параметров); градиента; наискорейшего спуска (рис.10.2).
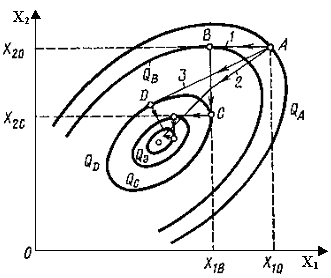
Рис.10.2. Способы движения к экстремуму
Метод Гаусса-Зейделя (рис.10.2, кривая 1) самый простой, но он не является кратчайшим. В методе градиента (рис.10.2, кривая 2) осуществляется одновременное изменение всех координат так, чтобы обеспечить движение САУ в направлении, близком к мгновенному направлению вектора градиента. Для этого способа характерно плавное движение к экстремуму и малый размах около точки экстремума. При способе наискорейшего спуска (рис.10.2, кривая 3) движение происходит по начальному направлению вектора градиента до тех пор, пока производная функции по этому направлению не обратится в нуль. Затем опять определяется направление градиента и происходит движение вдоль этого направления и т.д. Этот способ характеризуется быстрым выходом в зону экстремума, т.е. он предпочтителен в начале движения, а в районе экстремума целесообразно использовать метод градиента.
На рис.10.3 представлена система с запоминанием экстремума.
Рис.10.3. Блок-схема экстремальной САУ с запоминанием экстремума
Управляющее воздействие на линейную часть объекта (ЛЧО) системы формируется в результате выявления разности между текущим значением показателя качества и его экстремальным значением. В качестве регулятора (Р) чаще всего используется сервопривод. Для определения экстремального значения показателя качества используют запоминающее устройство (ЗУ), включаемое параллельно каналу, через который проходит сигнал текущего значения показателя качества. ЗУ реагирует только на увеличение сигнала Q (при максимуме). До тех пор, пока максимум не достигнут, сигналы, поступающие на элемент сравнения, равны и их разность равна нулю. После достижения экстремального значения Qmax показатель качества при дальнейшем увеличении сигнала X на входе экстремального звена будет уменьшаться. В результате этого появится сигнал на входе логического устройства (ЛУ), формирующий сигнал управления U=h0sign(Q-Qmax) и воздействующий на систему так, чтобы происходило уменьшение сигнала X и возрастание показателя качества Q. После срабатывания ЛУ сигнал поступает на стирание Qmax в ЗУ. Далее процесс поиска экстремума повторяется. Система с запоминанием экстремума является релейной, поэтому протекающие в ней процессы будут иметь колебательный характер. Амплитуда колебаний показателя качества определяется величиной зоны нечувствительности релейного элемента, формирующего сигнал управления в функции разности Q-Qmax.
Достоинством систем с запоминанием экстремума является сравнительно небольшая амплитуда колебаний параметров в процессе поиска. К недостаткам этих систем относится необходимость применения стабилизирующих устройств, входящих в ЛУ. Объясняется это тем, что при влиянии помех, например, смещающих экстремальную характеристику вверх, сигнал на входе ЛУ будет равен нулю, и изменения знака управляющего сигнала не произойдет. В результате этого принцип работы системы нарушается. Для обеспечения устойчивости работы системы используют специальные способы стабилизации. С целью улучшения процессов в экстремальных системах данного типа на вход ЗУ можно подавать кроме сигнала Q его производные и предусматривать соответствующие устройства связи выхода ЛУ с ЗУ. Системы с запоминанием экстремума наиболее целесообразны для малоинерционных объектов, имеющих высокочастотные помехи.
Основными показателями качества процессов поиска релейных одномерных экстремальных систем являются: время поиска экстремума, амплитуда и период колебаний, потери на поиск экстремума. Эти системы характеризуются наличием поисковых колебаний ("рысканий") около экстремума. Из рис.10.4,а устанавливаем, что при постоянной скорости изменения входной переменной в интервале 0.5T*i≤t≤T*i, X*=±K1t, где K1=tgα

Рис.10.4. Диаграмма "рыскания"
Период Т*i "рысканий" системы определяется моментом переключения реле рис.10.4,б. Тогда отклонение экстремального параметра на одном участке периода:
Q* = - K K12 t2.
Скорость изменения этого отклонения на участках между переключениями 0.5T*i≤t≤T*i определяется производной
dQ*/dt = - 2K K12 t.
Среднее за период поиска значение отклонения экстремального параметра называют потерей на поиск (рис.10.4,б):
D* = -K(K1T*i)2/12.
Амплитуда колебаний экстремального параметра получается подстановкой (рис.10.4,б) t = 0,5 T*i:
ΔQ* = - 0.25 K (K1 Т*i)2,
т.е. амплитуда "рысканий" в три раза больше потерь на "рыскание": ΔQ* = 3 D*.
Амплитуда колебаний и потери на поиск зависят от формы экстремальной характеристики и нелинейно зависят от периода колебаний.
Чтобы улучшить качество работы экстремальных систем, необходимо повысить их быстродействие (уменьшить время выхода на экстремум после смещения характеристики объекта), уменьшить амплитуду автоколебаний и снизить потери на поиск. Для этого применяют известные методы коррекции автоматических систем. Специфика экстремальных систем, имеющих нелинейные звенья, обусловливает сложность задач синтеза корректирующих устройств.
В ряде случаев для улучшения качества работы экстремальных систем используют инженерные рекомендации [22]. Например, для уменьшения времени поиска в системах с запоминанием экстремума и с коммутатором (рис.10.5) А. П. Юркевич предложил применять динамический преобразователь входного сигнала экстремального регулятора в виде реального дифференцирующего звена, который выполняет роль последовательного корректирующего устройства, включаемого между выходом одномерного объекта (О) и экстремальным регулятором (ЭР) - рис.10.5,а.
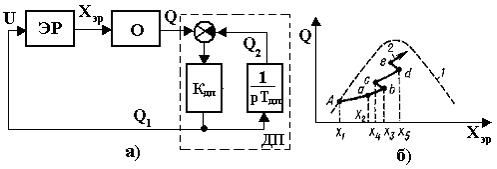
Рис.10.5. Динамический преобразователь
Структура динамического преобразователя (ДП) представлена в виде безынерционного звена, охваченного отрицательной обратной связью, содержащей идеальный интегратор [23]:
Wдп(р) = Кдп /(1+ (Кдп/рTдп)),
где Кдп и Тдп - коэффициент передачи и постоянная времени динамического преобразователя.
Рассмотрим процесс поиска экстремума системы с запоминанием экстремума и динамическим преобразователем (рис.10.5,6). Пусть начальная точка работы экстремальной системы после смещения характеристики Q(Xэр) соответствует точке А на кривой 1. В результате действия ЭР сигнал Xэр будет увеличиваться и при величине Х2 значение Q1 = Q (точка а). Затем, после того как Q2 станет больше Q, сигнал Q1 начнет уменьшаться. Это вызовет срабатывание ЭР при значении сигнала Хэр = Х3 (точка b), осуществляющего "ложный" реверс. Далее уменьшается сигнал Хэр до величины Х4, когда снова произойдет реверс ЭР (точка с). При значении Х5 осуществляется последующий "ложный" реверс ЭР (точка d) и т. д. Введение ложных реверсов ускоряет движение к экстремуму (см. кривую 2 на рис.10.4, б). Если характеристика Q (Хэр) дрейфует, то в результате действия ДП и ЭР система следит за смещением экстремума. Чем меньше инерционность объекта О, тем эффективнее действие ДП.
Для улучшения процессов поиска экстремума инерционных объектов высокого порядка, а также нейтральных и неустойчивых объектов В. В. Казакевичем предложен быстродействующий экстремальный регулятор - ЭРБ [22], в котором осуществляется поиск экстремума по максимуму производной (dQ/dt)max, реализуемый с помощью устройства формирования входного сигнала - УФС (рис.10.6,а), представляющего собой автоматический компенсатор. Скорость компенсации при этом настраивается соответственно свойствам объекта.
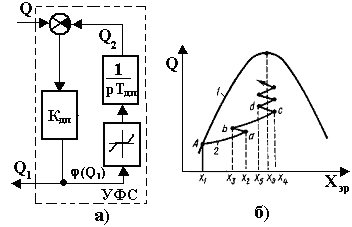
Рис.10.6. Устройство формирования сигналов
В отличие от динамического преобразователя УФС имеет нелинейную обратную связь (реверсивный двигатель автоматического компенсатора). На линейных участках характеристики Φ(Q1) структурная схема УФС эквивалентна структурной схеме ДП. В пределах зоны нечувствительности характеристики Φ(Q1) сигнал производной dQ/dt = 0. Это означает, что при медленном изменении сигнала Q (при медленном смещении Q (X) и при малом наклоне характеристики Q (X) вблизи экстремума) на вход экстремального регулятора будет поступать сигнал, пропорциональный параметру Q, без его производной. Следовательно, ЭРБ обеспечивает слежение за экстремумом при медленном изменении Q и форсированно выводит объект в область экстремума при быстром смещении характеристики Q (X).
Рассмотрим процесс поиска экстремума системы с ЭРБ и коммутатором. Пусть начальная точка работы экстремальной системы после смещения характеристики Q (Хэр) соответствует точке А на кривой 1 (рис.10.6,б). В результате действия коммутатора и УФС при значении X2 происходит ложный реверс (точка a), а при значении Хз - последующий реверс от действия УФС (точка b). При значении Хэр = Хэ производная dQ/dt достигает максимума. После того как Q2 станет больше нуля, сигнал Q1 уменьшится и при Хэр = Х4 ЭРБ произведет ложный реверс (точка c). Затем при Х5 произойдет реверс от действия УФС (точка d) и т. д. Система форсированно выводит объект в область экстремума (кривая 2 на рис.10.6,б). Вблизи экстремума при малой величине dQ/dt система перейдет на поиск экстремума по параметру Q. В процессе форсированного поиска система с ЭРБ не переходит на противоположную ветвь характеристики Q (Хэр), поэтому время поиска для инерционных объектов по сравнению с регуляторами без ЭРБ уменьшается на порядок без ухудшения качества установившихся режимов.
Рассмотренные основные методы улучшения качества работы экстремальных систем применяются при разработке как одномерных, так и многомерных систем.
Экстремальные системы с математической точки зрения являются нелинейными. При динамическом расчете СЭР второго порядка можно использовать метод фазовой плоскости. При повышении порядка дифференциальных уравнений, описывающих линейную часть, применяется метод гармонического баланса. Для снижения потери поиска применяются корректирующие устройства, охватывающие элементы и звенья системы гибкими обратными связями. В этом случае уменьшается амплитуда и повышается их частота.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обуче
Исследование САУ
| Метод динамического программирования Р.Беллмана
|  
|  
|  
| Метод динамического программирования Р.Беллмана [3,4,5] основан на принципе оптимальности, который формулируется так: оптимальное поведение обладает тем свойством, что, каковы бы не были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения. Чаще метод используется для численного решени
|









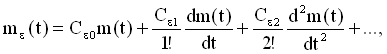 (9.18)
(9.18) 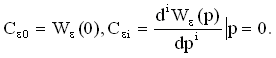
 (9.19)
(9.19)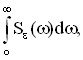 для чего подсчитывается площадь, заключенная между Sε(ω) и осью абсцисс;
для чего подсчитывается площадь, заключенная между Sε(ω) и осью абсцисс;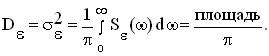

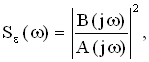 где А(jω) и B(jω) - полиномы, зависящие от АЧХ САУ и спектральной плотности возмущающего воздействия. Тогда для вычисления интеграла
где А(jω) и B(jω) - полиномы, зависящие от АЧХ САУ и спектральной плотности возмущающего воздействия. Тогда для вычисления интеграла (9.20)
(9.20)
 ; (9.21)
; (9.21) , (9.22)
, (9.22) ; (9.23)
; (9.23)  . (9.24)
. (9.24) , (9.25)
, (9.25) 0 и S(ω)= const. В этом случае для вычисления интеграла от спектральной плотности ошибки (9.25) возможно использование аналитического метода [2,19]. А если спектральная плотность входного воздействия задана графически, то целесообразно использование для анализа и синтеза графоаналитического метода. Он наглядно показывает, что ошибка регулирования зависит от взаимного расположения графиков спектральной плотности воздействия и а.ч.х. передаточной функции ошибки САУ. Ранее было показано, что для снижения дисперсии ошибки необходимо разносить их максимумы, снижать пик а.ч.х., т.е. получать систему более узкополосной и достаточно задемпфированной.
0 и S(ω)= const. В этом случае для вычисления интеграла от спектральной плотности ошибки (9.25) возможно использование аналитического метода [2,19]. А если спектральная плотность входного воздействия задана графически, то целесообразно использование для анализа и синтеза графоаналитического метода. Он наглядно показывает, что ошибка регулирования зависит от взаимного расположения графиков спектральной плотности воздействия и а.ч.х. передаточной функции ошибки САУ. Ранее было показано, что для снижения дисперсии ошибки необходимо разносить их максимумы, снижать пик а.ч.х., т.е. получать систему более узкополосной и достаточно задемпфированной.

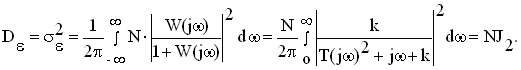
 где
где 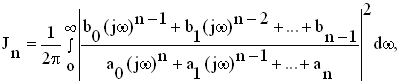
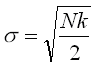 .
. ,
, т.е. САУ оптимальная по быстродействию, если обеспечивается минимум этого интеграла с учетом ограничений. Принимаются также известные в ТАУ интегральные оценки качества переходного процесса, например, квадратичный. В качестве критерия оптимальности систем при случайных воздействиях используют среднее значение квадрата ошибки системы
т.е. САУ оптимальная по быстродействию, если обеспечивается минимум этого интеграла с учетом ограничений. Принимаются также известные в ТАУ интегральные оценки качества переходного процесса, например, квадратичный. В качестве критерия оптимальности систем при случайных воздействиях используют среднее значение квадрата ошибки системы  При управлении от источников с ограниченной мощностью берут функционал, характеризующий расход энергии на управление
При управлении от источников с ограниченной мощностью берут функционал, характеризующий расход энергии на управление  где u(t) и i(t) - напряжение и ток цепи управления. Иногда в качестве критерия оптимальности сложных САУ принимают максимум прибыли технологического процесса I=
где u(t) и i(t) - напряжение и ток цепи управления. Иногда в качестве критерия оптимальности сложных САУ принимают максимум прибыли технологического процесса I= 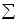 giПi - S, где gi - цена продукта; Пi - производительность; S - затраты.
giПi - S, где gi - цена продукта; Пi - производительность; S - затраты.








