
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические исследования в задачах оценки точностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим процесс обеспечения точности совокупности деталей - партии (или нескольких партий) с целью найти закономерности, которые могут быть использованы как при оценке технологического процесса механической обработки заготовок в отношении точности, так и при технологическом обеспечении (а также контроле) точности. Подобные исследования и определение точности механической обработки основываются на положениях теории вероятностей и математической статистики. В соответствии с этой теорией все погрешности, возникающие при изготовлении заготовок, деталей и их оборке, разделяются на три вида: - систематические постоянные; - систематические закономерно изменяющиеся; - случайные. Систематические постоянные погрешности не изменяются при обработке всех деталей партии или нескольких партий деталей и возникают вследствие постоянно действующих факторов: - неперпендикулярность оси отверстия плоскости основания детали - кронштейна, - вследствие неперпендикулярности оси шпинделя плоскости стола станка; - конусообразность вала - из-за не параллельности оси шпинделя направляющих станка; - неточность расстояния между осями отверстий - из-за неточности кондуктора; - неточность диаметра отверстия - из-за неточности развертки. Такие погрешности легко выявляются пробными проходами или испытаниями оснастки или инструмента и устраняются соответствующими способами. Систематические, регулярно изменяющиеся погрешности могут влиять на точность непрерывно или периодически. На основе результатов исследования выявляется закон действия таких погрешностей на точность размеров и формы деталей и принимаются соответствующие меры к их уменьшению или исключению. Случайные погрешности возникают в результате действия большого числа не связанных между собой факторов, например, колебания величины припуска на механическую обработку, твердости заготовок, усилия закрепления заготовок приводят к изменениям усилия резания Рy и величины отжатия Y, т.е. изменяется жесткость системы СПИД и как следствие - точность обработки каждой детали в партии как в отношении выдерживаемых размеров, так и формы и взаимного расположения поверхностей. Связь между случайными погрешностями и вызывающими их появление факторами может быть установлена двумя методами:
- аналитическим; - статистическим. Аналитический расчет может быть выполнен при явно выраженной связи между случайной погрешностью и вызывающими ее появление факторами. Пределы изменения случайной величины, например, колебания размера предельных расстояний от поверхности измерительной базы до обрабатываемой поверхности можно заранее вычислить, зная допуск на размер заготовки. При неявно выраженной связи пределы изменения случайной величины могут быть установлены экспериментально. При аналитическом расчете результирующей погрешности
Аналитические расчеты погрешностей сложны и весьма трудоемки и не всегда, выполнимы в производственных условиях. Поэтому такие расчеты применяются главным образом при составлении типовых нормативов точности механической обработки, которыми пользуются технологи, иногда как исходными ориентировочными, иногда как окончательными данными при выборе способа обработки, оборудования, оснастки, инструмента при проектировании технологического процесса механической обработки. Наиболее широко для определения точности, корректировки действующего технологического процесса механической обработки, для его контроля применяется статистический метод. Статистический метод расчета точности обработки применим в условиях изготовления большого числа (не менее 50) одинаковых деталей, обрабатываемых как на настроенных станках (главным образом), так и методом пробных проходов и промеров. Сущность этого метода в том, что по замерам исследуемых размеров строятся кривые распределения фактических размеров и обрабатываются в соответствии с теорией вероятностей и математической статистики. Кривые распределения строятся так: всю совокупность измерений интересующего нас размера в партии деталей разбивают на ряд групп. В каждую группу входят величины размеров, результаты измерений которых находятся в пределах установленного интервала (количество интервалов берется в пределах 7…II). Величины интервалов откладывают по оси абсцисс (рис.4.1), а по оси ординат - количество деталей, размеры которых находятся в пределах каждого интервала (частоту т или отношение mк количеству деталей в партии n, т.е. m/n - частость). После соединения нанесенных точек получают кривуюраспределения, определяющую полигон
Рис.4.1 Полигон рассеяния размеров Диапазон предельных значений отклонений от настроечного размера (в пределах от минимального до максимального) представляет поле рассеивания. Эта величина может служить приближенной мерой точности исследуемого процесса. Чем меньше поле рассеивания, тем точнее исследуемый технологический процесс. Вид кривой рассеивания определяется количеством и характером факторов, влияющих на исследуемую величину. При различных условиях обработки заготовок рассеивание их действительных размеров подчиняется различным математическим законам. Многочисленные исследования показали, что распределение действительных размеров заготовок на настроенных станках, чаще всего подчиняется закону нормального распределения (закону Гаусса). Теоретическое обоснование этого положения вытекает из выполнения условий действия закона нормального распределения при обработке деталей из заготовок. Влияние каждого сказывающегося на точности обработки слагаемого на сумму ничтожно мало и примерно одинаково, т.е. среди слагаемых нет доминирующих, и в состав суммы входит большое число взаимно независимых случайных величин. Соответствие закону нормального распределения тем точнее, чем больше слагаемых в сумме. При механической обработке это условие соблюдается, поскольку результирующая погрешность обработки обычно представляет собой сумму большого числа погрешностей, зависящих от точности станка, приспособления, инструмента и заготовки. Эти погрешности, как видно из ранее приведенного анализа причин, вызывающих погрешности размеров и формы деталей, по существу представляющих собой взаимно независимые случайные величины, влияние каждой из которых на результирующую погрешность имеет один порядок. Уравнение кривой нормального распределения: У= где
m - частота (количество заготовок данного интервала размеров); n - количество деталей в партии; е - основание натуральных логарифмов. Кривая, характеризующая закон нормального распределения (закон Гаусса), показана на рис. 4.2. Среднее арифметическое Lср действительных размеров деталей партии характеризует положение центра группирования. Анализ кривой распределения (рис.4.2) показывает: а) кривая нормального распределения симметрична относительно оси ординат (Li = Lср); б) на расстоянии ± в) кривая асимптотически приближается к оси абсцисс. На расстоянии ± 3 г) среднее квадратическое отклонение
Поскольку практически принято считать, что на расстоянии δ > 6σ, (4.4) где δ - допуск на исследуемый размер
Рис.4.4. Соотношения между допуском и полем рассеяния
На рис.4.4 показаны возможные соотношения величин 6 При правильном построении технологического процесса по мере перехода от обдирочной к получистовой, чистовой и отделочной обработке величина σдолжна уменьшаться, как показано на риc.4.5, т.е. σ > σ1 > σ2 > σ3.
Таким образом, построение кривых распределения дает информацию о правильности построения технологического процесса и настройки станка на заданный размер. Однако в процессе обработки партии заготовок под действием тех или иных факторов может возникнуть опасность появления брака (сбилась настройка, износился инструмент, изменилась твердость заготовок или величина припуска на их обработку). Периодическое построение кривых распределения в условиях серийного или массового производства еще при отсутствии брака может выявить тенденцию изменения размеров относительно настроечного размера, как показано на рис.4.6, и тем самым предупредить брак.
Рис. 4.6. Если исходная кривая распределения I (рис. 4.6, а) через некоторое время становится более пологой кривая (II), это свидетельствует о появлении случайных погрешностей, снижающих точность обработки; следует проверить твердость и размеры заготовок, состояние станка, приспособления. Если кривая распределения при неизменной ее форме через некоторое время с момента начала работы сместилась (рис.4.6,б) - это свидетельствует об изменении настроечного размера и необходимости его корректировки. Именно эти свойства и возможности статистического метода оценки точности положены в основу статистического контроля на производстве. Одно из его достоинств - возможность профилактики брака. При механической обработке в зависимости отвида, характера и условий выполнения тех или иных операций распределение размеров обрабатываемых деталей подчиняется не только закону нормального распределения, но и другим законам. Так, если на выполняемый размер оказывает влияние систематическая, постепенно возрастающая погрешность (например, износ инструмента), подчиняющаяся закону прямой пропорциональной зависимости, то распределение размеров происходит по закону равной вероятности (рис.4.7, а).
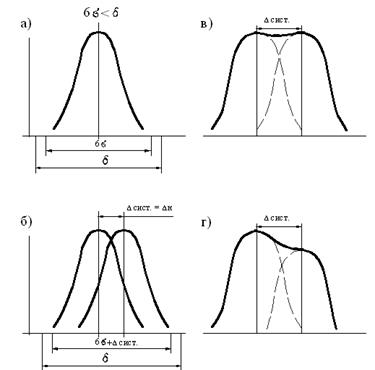
Рис.4.7 Если на выполняемый размер влияет закономерно изменяющаяся погрешность, возрастающая первоначально замедленно, а затем ускоренно, то распределение размеров происходит по закону треугольника (закон Симпсона) - рис. 4.7, б. Такое распределение может иметь место при совместном действии размерного износа инструмента с сильно выраженной фазой начального износа и увеличением силы резания в конце периода стойкости инструмента в результате прогрессирующего его затупления. Если на выполняемый размер влияет температурная деформация обрабатываемой заготовки, то кривая распределения размеров принимает вид кривой, показанной на рис. 4.7, в. При обработке заготовок на станках на точность их размеров часто одновременно воздействуют разные причины, вызывающие появление как случайных погрешностей, образующихся по разным законам, так и систематических погрешностей. В подобных случаяхзакон распределения размеров обрабатываемых деталей представляет собой композицию нескольких законов распределения и кривая нормального распределения (рис.4.8,а), удовлетворяющая условию работы без брака (6σ > δ), смещается на величину систематической погрешности Δсист(рис.4.8,б).
Рис.4.8. При этом условие работы без брака будет иным: (6σ + Δсист) < δ, (4.5) Например, при смене разверток характер первоначальной кривой распределения остается неизменным (условия обработки неизменны), однако вершина кривой распределения сместится на величину разности диаметров первой и второй разверток Δн = Δсист(рис.4.8,б) Если кривая распределения строится при этом по замерам деталей без учета систематической погрешности (например, когда изменяются размеры всей партии деталей, обработанных с нескольких настроек), то форма общей кривой искажается в сравнении с кривой Гаусса (рис. 4.8., а). Кривая может иметь несколько вершин одинаковой (рис. 4.8., в) или разной (рис. 4.8., г) высоты соответственно числу настроек и количеству заготовок, обработанных с каждой настройки. При вычислении суммарной погрешности обработки систематические погрешности складываются алгебраически, т.е. с учетом знаков. Поэтому результат суммирования может показать нетолько увеличение, но и снижение общей погрешности за счет взаимной компенсации влияния составляющих погрешностей. Определение вероятного процента брака. В тех случаях, когда нарушено условие работы без брака (6 σ < δ), т.е. когда поле рассеивания размеров деталей превосходит поле допуска (6σ > δ ), появляется вероятность брака, величину которой необходимо установить. В ряде случаев на производстве идут на небольшой риск получения брака, в частности, когда потери из-за брака полностью окупаются значительным сокращением себестоимости обработки, упрощением технологического процесса и сокращением его цикла. Вероятный процент брака всей партии обработанных деталей вычисляют следующим образом. Принимают с погрешностью не более 0,27%, что все детали партии имеют действительные размеры в пределах поля рассеивания 6σ =
Рис.4.9. Определение вероятности появления брака Тогда площадь заштрихованных участков представляет собой количество заготовок (в долях единицы или в процентах), размеры которых выходят за пределы допуска. Для определения количества годных деталей необходимо найти площадь, ограниченную кривой и осью абсцисс, на длине, равной полю допуска δ = При симметричном расположении поля рассеивания относительно поля допуска (рис.18, а) следует найти удвоенное значение интеграла, определяющего половину площади, ограниченной кривой Гаусса и абсциссой Х о. Это значение определяют по формуле Фz = где Z=
Значение функции Фz зависит от отношения Z=
Нет необходимости вычислять значения этой функции в каждом случае - они табулированы и представлены в справочниках. Приведем пример определения количества бракованных деталей при обработке на револьверном станке партии латунных валиков, состоящей из 300 штук. Допуск на обработку δ= 0,1 мм. Материал резца – алмаз (износ за время обработки одной партии деталей пренебрежимо мал). Определим количество годных и бракованных деталей для случая, когда настройка станка обеспечивает симметричное расположение кривой распределения по отношению к полю допуска (рис.4.9,а). По результатам замеров 75 штук пробных деталей эмпирическая величина среднего квадратического отклонения размеров S= 0,02 мм. Решение 1 Считаем, что распределение размеров подчиняется закону Гаусса (обработка на настроенном станке при отсутствии доминирующих и систематических погрешностей). 2 Определим расчетное значение среднего квадратического отклонения по формуле 3 Зона фактического рассеивания А = 6σ = 6 * 0,025 = 0,15 мм 4 Согласно расчету X0 = Для всей партии количество годных деталей составило 95,44% или 286 штук, а бракованных, соответственно, 4,56%, или 14 штук. В практике на основе результатов подобных расчетов для предотвращения появления брака принимают меры, приводящие к уменьшению случайного рассеивания размеров (уменьшению б). Этого можно добиться за счет использования точного оборудования, наиболее совершенных точных методов обработки и рационального построения технологического процесса, применения инструмента высокой стойкости. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. На какие виды делятся погрешности, возникающие при обработке заготовок? 2. За счет чего возникают случайные погрешности при обработке? 3. Каким законом описывается распределение действительных размеров заготовок на настроенных станках? 4. Как определяется запас по точности? 5. Каким способом определяется количество бракованных деталей при обработке?
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1403; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.48.148 (0.015 с.) |

 первичные погрешности (
первичные погрешности ( ), получаемые предварительным расчетом или экспериментально складываются алгебраически, если они систематические, и по формуле (17), если они случайные.
), получаемые предварительным расчетом или экспериментально складываются алгебраически, если они систематические, и по формуле (17), если они случайные.
 (4.1)
(4.1) рассеяния размеров.
рассеяния размеров.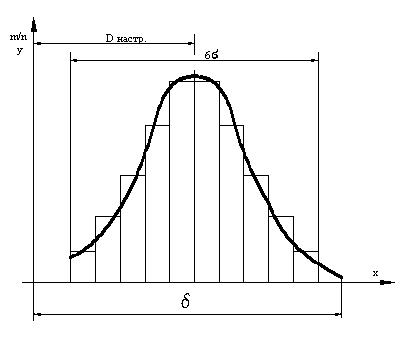
 , (4.2)
, (4.2) - среднее квадратическое отклонение
- среднее квадратическое отклонение
 , (4.3)
, (4.3) от вершины кривая имеет две точки перегиба (А и В);
от вершины кривая имеет две точки перегиба (А и В);

 3σ от вершины кривой ветви пересекаются с осью абсцисс и в этих пределах заключена вся площадь кривой (100%),т.е. все размеры деталей партии находятся в пределах
3σ от вершины кривой ветви пересекаются с осью абсцисс и в этих пределах заключена вся площадь кривой (100%),т.е. все размеры деталей партии находятся в пределах 
 Рис.4.5. Изменение среднего квадратического отклонения
Рис.4.5. Изменение среднего квадратического отклонения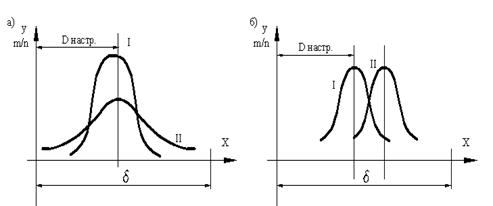

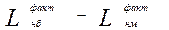 . Считается, что площадь, ограниченная кривой нормального распределения и осью абсцисс (рис.4.9), равна единице и выражает собой 100% деталей партии.
. Считается, что площадь, ограниченная кривой нормального распределения и осью абсцисс (рис.4.9), равна единице и выражает собой 100% деталей партии.

 , (4.6)
, (4.6)
 (4.7)
(4.7) = 0,05 мм и Z = 2,0. Следовательно, Ф(Z} = 0,4772, что соответствует 4 7,72% годных деталей от половины всей партии (функция Ф(Z) определена от 0 до X 0).
= 0,05 мм и Z = 2,0. Следовательно, Ф(Z} = 0,4772, что соответствует 4 7,72% годных деталей от половины всей партии (функция Ф(Z) определена от 0 до X 0).


