
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 2. Моделирование дискретных объектов и процессовСодержание книги
Поиск на нашем сайте
Использование множеств для моделирования технических систем Дискретная математика имеет широкий спектр приложений, прежде всего в областях, связанных с информационными и компьютерными технологиями. Понятия «множества», «отношения», «функции» и близкие к ним составляют основной словарь дискретной математики. Представление окружающего мира в виде множества отдельных объектов позволяет сформировать доступную для рационального анализа модель. Понятие множества как любое другое исходное понятие математической теории не определяется. Можно сказать, что множество – это любая определенная совокупность объектов. Объекты, из которых составлено множество, называются его элементами. Элементы множества различимы и отличимые друг от друга. Пример. Множество S страниц в книге, множество N натуральных чисел (1, 2, 3,..), множество C станков в цехе и т.д. Обычно множества обозначаются прописными буквами латинского алфавита, а элементы множества – строчными буквами. Если объект x является элементом множества М, то говорят, что x принадлежит М (x Î M). В противном случае говорят, что х не принадлежит М (х Ï М). Множество, не содержащее элементов, называют пустым (обозначение Ø). Множества могут быть конечными (состоять из конечного числа элементов) или бесконечными. Число элементов в конечном множестве называется мощностью множества и обозначается ½М½. Множество А называется подмножеством множества М, если каждый элемент А является элементом М (А Í М). Знак Í называется знаком включения. Множества А и М равны, если их элементы совпадают, иначе говоря, если А Í М и М Í А. Множество может быть задано перечислением его элементов, например А = {а1, а2, …,аn}. Если известна процедура, описывающая способ получения элементов множества из уже полученных элементов или из других объектов, то множества могут быть заданы: Характеристическим предикатом М:= {х | Р(х)}; Порождающей процедурой М:= {х | х = f} Пример 1 М9 := {1,2,3,4,5,6,7,8,9}; 2 М9 := {n | n Є N &n<10}; 3 М9 = {n | for n from 1 to 9}. Перечислением можно задавать только конечные множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.
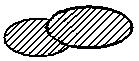
Операции над множествами. Самого по себе понятия множества еще недостаточно – нужно определить способы конструирования новых множеств из уже имеющихся, то есть совершать операции над множествами. Обычно рассматриваются следующие операции: 1 Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В. Символически это записывается так
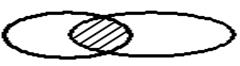
Аналогично определяется объединение произвольной совокупности множеств. В общем случае можно использовать обозначение È А, которое формулируется как объединение всех множеств А, принадлежащих совокупности М. Пример. Сборочная единица представляет собой объединение некоторого множества Т-систем «деталь» СЕ = È ТСД 2 Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые одновременно принадлежат и А и В. Символически это записывается так
Аналогично определяется пересечение произвольного числа множеств.
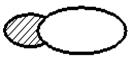
А \ В = {C ê C Î А и C Ï В }
В отличие от двух предыдущих операций разность строго двухместна, т.е. определена только для двух множеств и не коммутативна: А \ В ¹ В \ А Симметричная разность множеств А и В это множество. стоящее из элементов, которые принадлежат хотя бы одному из множеств А и В, но без элементов, которые одновременно принадлежат множествам А и В. А Δ В= (А U B) \ (A ∩ B)= {X | (X Є A и Х ÏВ) или (ХÏ А и е Є В)} А В
Отношения Обычно широко используемое понятие «отношение» имеет вполне определенное математическое значение. Прямым произведением множеств А и В называется множество пар (а,в),таких что а Î А, в Î В. А*В:= {(а,в) | а Є А и в Є В} Для представления множеств в программах, реализуемых на ЭВМ, необходимо описать в терминах используемой системы программирования структуру данных, используемую при исследовании объектов. Предполагается, что в системе программирования доступны такие структуры данных, как массивы, записи и указатели. Таким образом, применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других операций. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, вида и относительной частоты использования операций в конкретной задаче и т.д. Умение выбрать подходящее для конкретного случая представление является творческой задачей практического программирования. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. При каком условии множество может быть представлено характеристическим предикатом? 2. Перечислите основные операции над множествами?
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 604; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |


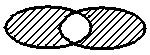 А Δ В
А Δ В


