
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория вероятности при оценке надежности технических системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оценки надежности работы технических систем используются законы теории вероятности. Рассмотрим, как осуществляется статистическая обработка результатов испытаний и определение показателей надежности. Для решения задач по оценке надежности и прогнозированию работоспособности объекта необходимо иметь математическую модель, которая представлена аналитическими выражениями одного из показателей P(t) или f(t) или Выясним, как изменяется безотказность объектов при их эксплуатации, что позволит классифицировать модели и определить возможности их применения. Опыт эксплуатации показывает, что изменение интенсивности отказов
Рис.4.10
Кривую можно условно разделить на три характерных участка: первый – период приработки, второй – период нормальной эксплуатации, третий – период старения объекта. Период приработки объекта имеет повышенную интенсивность отказов (ИО), вызванную отказами в начальный период приработки, обусловленными дефектами производства, монтажа, наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем. В период нормальной эксплуатации ИО уменьшается и практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего из-за несоблюдения условий эксплуатации, случайных изменений нагрузки, неблагоприятных внешних факторов и т. п. Именно этот период соответствует основному времени эксплуатации объекта. Возрастание ИО относится к периоду старения объекта и вызвано увеличением числа отказов от износа, старения и других причин, связанных с длительной эксплуатацией. Вид аналитической функции, описывающей изменение показателей надежности P(t), f(t) или Рассмотрим, как осуществляется статистическая обработка результатов испытаний и определение показателей надежности.
В результате испытаний N невосстанавливаемых одинаковых объектов получена статистическая выборка – массив наработки до отказа (в любых единицах измерения) каждого из N испытывавшихся объектов. Выборка характеризует случайную величину наработки до отказа объекта T = {t}. Необходимо выбрать закон распределения случайной величины T и проверить правильность выбора по соответствующему критерию. Подбор закона распределения осуществляется на основе аппроксимации (сглаживания) экспериментальных данных о наработке до отказа, которые должны быть представлены в наиболее компактном графическом виде. Выбор той или иной аппроксимирующей функции носит характер гипотезы, которую выдвигает исследователь. Экспериментальные данные могут с большим или меньшим правдоподобием подтверждать или не подтверждать справедливость той или иной гипотезы При большом числе испытываемых объектов полученный массив наработок { …, ti, … } является громоздкой и мало наглядной формой записи случайной величины T. Поэтому для компактности и наглядности выборка представляется в графическом изображении статистического ряда – гистограмме наработки до отказа. Для этого необходимо: - установить интервал наработки [ tmin, tmax ] и его длину - разбить интервал наработки [ tmin, tmax ] на k интервалов равной ширины
- подсчитать частоты появления отказов во всех k интервалах
где Очевидно, что
- полученный статистический ряд представляется в виде гистограммы, которая строится следующим образом. По оси абсцисс (t) откладываются интервалы
Рис. 4.11
Используя данные сформированного статистического ряда, определяются статистические оценки показателей надежности, т. е. эмпирические функции: - функция распределения отказов (оценка РО )
- функция надежности (оценка ВБР)
Рис. 4.12
- плотность распределения отказов (оценка ПРО)
- интенсивность отказов (оценка ИО)
Рис. 4.13
Рис. 4.14
На рис. 4.12, 4.13, 4.14 приведены соответственно графики статистических оценок Правила построения графиков ясны из приведенных выше расчетных формул. Каждый из графиков имеет свой масштаб. Для расчета статистических оценок числовых характеристик можно воспользоваться данными сформированного статистического ряда. Обычно определяются следующие показатели: - оценка средней наработки до отказа (статистическое среднее наработки):
- оценка дисперсии наработки до отказа (эмпирическая дисперсия наработки):
где Оценка СКО Целесообразно рассчитать также оценки и некоторых вспомогательных характеристик рассеивания случайной величины T: - выборочный коэффициент асимметрии наработки до отказа
- выборочный эксцесс наработки до отказа
Эти характеристики используются для выбора аппроксимирующей функции. Так коэффициент асимметрии является характеристикой «скошенности» кривой распределения, например, если распределение симметрично относительно МО (математического ожидания), то A = 0. На рис. 4.15,а распределение f2(t) имеет положительную асимметрию A > 0, а f3(t) – отрицательную A < 0. Эксцесс характеризует «крутость» (остро- или плосковершинность) распределения. Для нормального распределения E = 0. Кривые f(t), более островершинные по сравнению с нормальной, имеют E > 0, а наоборот – более плосковершинные, E < 0 (рис.4.15, б).
Рис.4.15. Кривые распределения
Выбор закона распределения состоит в подборе аналитической функции наилучшим образом аппроксимирующей эмпирические функции надежности. Выбор, в значительной мере, процедура неопределенная и во многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы, а также анализа вида графиков Очевидно, что выбор распределения будет зависеть, прежде всего, от вида эмпирической функции плотности распределения отказов Итак, выбор закона распределения носит характер принятия той или иной гипотезы. Предположим, что по тем или иным соображениям, выбран гипотетический закон распределения, заданный теоретической функцией плотности распределения отказов
где a, b, c, … - неизвестные параметры распределения. Требуется подобрать эти параметры так, чтобы функция f(t) наилучшим образом сглаживала ступенчатый график На графике вместе с
Критерий согласия используется для проверки гипотезы о том, что случайная величина T, представленная своей выборкой, имеет распределение предполагаемого типа.
Проверка состоит в следующем. Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной. Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим. Если согласованность очень мала, то гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную. В противном случае – экспериментальные данные не противоречат принятому распределению. Из известных критериев наиболее применяемый критерий согласия Проверка согласованности распределений по критерию - рассчитывается критерий
где - определяется число степеней свободы R = k – L, где L – число независимых условий, наложенных на частоты а) условие б) условие совпадения в) условие совпадения Чаще всего L = 3. Чем больше число степеней свободы, тем больше случайная величина - по рассчитанным На практике, если P < 0,1, то рекомендуется подыскать другой закон распределения. В целом, с помощью критерия согласия, можно опровергнуть выбранную гипотезу, если же P достаточно велика, то это не может служить доказательством правильности гипотезы, а указывает лишь на то, что гипотеза не противоречит данным эксперимента.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Как получается модель для оценки надежности работы технических систем? 2. Какие периоды выделяются в зависимости, описывающей изменение интенсивности отказов работы объектов? 3. Для какой цели используется критерий согласия? Планирование эксперимента Под экспериментом будем понимать совокупность операций совершаемых над объектом исследования с целью получения информации об его свойствах. Эксперимент, в котором исследователь по своему усмотрению может изменять условия его проведения, называется активным экспериментом. Если исследователь не может самостоятельно изменять условия его проведения, а лишь регистрирует их, то это пассивный эксперимент. Важнейшей задачей методов обработки полученной в ходе эксперимента информации является задача построения математической модели изучаемого явления, процесса, объекта. Ее можно использовать и при анализе процесс
ов и при проектировании объектов. Можно получить хорошо аппроксимирующую математическую модель, если целенаправленно применяется активный эксперимент. Другой задачей обработки полученной в ходе эксперимента информации является задача оптимизации, т.е. нахождения такой комбинации влияющих независимых переменных, при которой выбранный показатель оптимальности принимает экстремальное значение. Опыт – это отдельная экспериментальная часть. План эксперимента – совокупность данных определяющих число, условия и порядок проведения опытов. Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления. В процессе измерений, последующей обработки данных, а также формализации результатов в виде математической модели, возникают погрешности, и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить о ее адекватности. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами. Цель планирования эксперимента – нахождение таких условий и правил проведения опытов, при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Итак, для получения математической модели изучаемого процесса необходимо проводить эксперимент. Количество опытов должно быть минимальным, но достаточным для адекватного отражения изучаемого процесса в создаваемой математической модели. С этой целью составляется план полного факторного эксперимента (ПФЭ). Количество опытов в плане составит 2n, где n - число независимых переменных (факторов). Для плана ПФЭ 22 число факторов равно двум (n =2) и число уровней фиксирования факторов также 2. Если заранее не известно аналитическое выражение функции отклика, то можно рассматривать не саму функцию, а ее разложение, например в степенной ряд в виде полинома
Y=В0 + B1Х1 + … + BnХn + В12Х1Х2 + … Вnn-1ХnХn-1 + В11Х12 + … + ВnnXn2 +….
Разложение в степенной ряд функции возможно в том случае, если сама функция является непрерывной и гладкой. На практике обычно ограничиваются числом членов степенного ряда и аппроксимируют функцию полиномом некоторой степени. Факторы могут иметь разные размерности (А, В, Вт, об/мин) и резко отличаться количественно. В теории планирования эксперимента используют кодирование факторов.
Рис. 4.16. Пространство кодированных факторов
Эта операция заключается в выборе нового масштаба для кодированных факторов (рис. 4.16), причем такого, чтобы минимальное значение кодированных факторов соответствовало “-1”, а максимальное значение “+1”, а также в переносе начала координат в точку с координатами Х1ср, Х2ср, …, Хnср
Текущее значение кодированного фактора
где Хi – именованное (абсолютное) значение фактора; xi – кодированное значение фактора; Xicp -Ximin =Ximax-Xicp - интервал варьирования фактора. Полное число возможных сочетаний значений n факторов (число опытов, а значит и число строк плана) N =22=4. Составляется план, в котором число столбцов факторов и их сочетаний равняется числу членов уравнения. Так для уравнения
План ПФЭ 22 для этого уравнения представляется в следующем виде.
Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбцы, не обведенные утолщенной рамкой, при проведении опытов носят вспомогательный характер. В первый столбец (i =0) во все четыре ячейки заносятся +1. Во второй столбец (i =1) заносятся единицы с чередующими знаками (начинаем с -1). В этом случае сумма элемента столбца равняется нулю. Третий столбец заполняем единицами с чередующимися через 2 элемента знаками. Сумма элементов также равняется нулю. Геометрическое отображение плана ПФЭ 22 с указанием номеров точек плана в факторном пространстве представлено на рис. 4.17. Точки плана располагаются в вершинах квадрата.
Рис. 4.17 Геометрическое отображение плана ПФЭ 22 в факторном пространстве Элементы столбцов, соответствующих произведениям факторов получаются путем перемножения элементов предыдущих столбцов. Такое правило позволяет гарантировать, что мы не пропустили ни одного возможного сочетания факторов в опытах и в то же время не будет повторений одинаковых сочетаний. Последние два столбца факторов, соответствующие квадратам факторов, состоят только из +1. Столбцы, обведенные утолщенной рамкой, образуют план эксперимента. Столбец х1х2, не обведенный утолщенной рамкой, при проведении опытов носит вспомогательный характер. Особенности плана ПФЭ 22: 1. Различных столбцов в таблице получилось лишь четыре. Столбцы, соответствующие квадратам факторов неотличимы от столбца х 0 - это общий результат для плана ПФЭ 2n. Это не позволяет определить отдельно коэффициенты при квадратах факторов. Поэтому планы ПФЭ 2n называют планами первого порядка. Для определения коэффициентов при квадратах факторов используют планы второго порядка. В дальнейшем в планах ПФЭ 2n столбцы квадратов факторов изображаться не будут. 2. Число различных столбцов равняется числу различных сочетаний факторов, то есть числу строк плана - числу опытов N. Это тоже общий результат для этих планов, то есть с помощью планов ПФЭ 2n можно определить все коэффициенты линейного полинома со всеми возможными сочетаниями факторов, включая коэффициенты b12…n, отражающие максимальное взаимодействие факторов вида х1х2…хn. 3. В плане ПФЭ 22 сумма квадратов элементов любого столбца
Поэтому для планов ПФЭ 2n
Таким образом, с помощью планов ПФЭ 2n можно определить свободный член уравнения b0,
План ПФЭ 2n может являться насыщенным, при выборе числа членов уравнения m + 1 = N, ненасыщенным, при выборе числа членов уравнения и соответственно числа столбцов плана m + 1 < N. План ПФЭ 2n является также рототабельным, так как все точки плана лежат на окружности (сфере, гиперсфере) с радиусом Поскольку фиктивная переменная во всех опытах имеет максимальное значение, то для вычисления свободного члена формула имеет вид: b0 = Σ Yj / N. Все коэффициенты регрессии определяются независимо друг от друга. Это свойство приводит к тому, исключение из плана эксперимента тех или иных факторов не потребует проведения все расчетной работы заново. Для плана ПФЭ 23 число факторов n = 3. Выполняется N = 23 = 8 опытов. Уравнение может содержать до восьми членов
Таким образом, формируется план из восьми строк и восемь столбцов. В четвертом столбце (i =3) записываются единицы с чередующимися знаками через четыре элемента. План составляется аналогичным образом плану ПФЭ 22.
Геометрическое отображение плана ПФЭ 23 с указанием номеров точек плана в факторном пространстве представлено на рис. 4.18. Точки плана располагаются в вершинах куба.
Рис. 4.18 Геометрическое отображение плана ПФЭ 23 в факторном пространстве Пример применения плана ПФЭ 22. Пусть в результате проведения экспериментов по плану ПФЭ 22, то есть при изменении двух факторов, мы получили опытные значения Y1, Y2, Y3, Y4. Поверхность, уравнение которой нас интересует, имеет вид рис. 4.19
Рис. 4.19. Поверхность функции отклика
Составляем план ПФЭ 22
Вначале найдем коэффициенты сокращенного линейного полинома вида
и результаты вычислений Рассчитываем коэффициенты полинома.
Полином имеет вид
Результаты расчета по нему приведены в соответствующем столбце плана. Наблюдаются расхождения между Y и
При этом ранее определенные коэффициенты остаются без изменений. Определим коэффициент при дополнительном члене полинома
Полином имеет вид
По нему рассчитываем предсказанные значения отклика в точках плана (столбец
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ: 1. Что называется активным экспериментом? 2. В чем заключается операция кодирование факторов? 3. В каком случае возможно разложение в степенной ряд функции отклика? 4. Как определяются коэффициенты линейного полинома?
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 644; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.216 (0.015 с.) |

 (t). Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями.
(t). Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями.
 , где
, где 
 t – шаг гистограммы
t – шаг гистограммы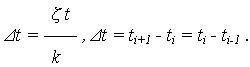
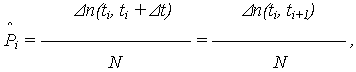

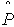 . Возможный вид гистограммы приведен на рис. 4.11.
. Возможный вид гистограммы приведен на рис. 4.11.







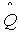 (t), P(t), f(t)и
(t), P(t), f(t)и 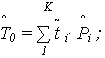
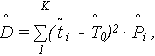
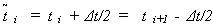 – середина i-го интервала наработки, т. е. среднее значение наработки в интервале.
– середина i-го интервала наработки, т. е. среднее значение наработки в интервале.



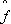 (t),
(t),  (t).
(t).
 (t) строится теоретическая функция плотности распределения отказов f(t), что позволяет визуально оценить результаты аппроксимации (расхождения между
(t) строится теоретическая функция плотности распределения отказов f(t), что позволяет визуально оценить результаты аппроксимации (расхождения между  2 Пирсона.
2 Пирсона.
 – теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti +
– теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti +  ;
; ;
; = D и т. д.
= D и т. д.
 .
. ,
,


 ,
, .
. коэффициентов bi,
коэффициентов bi, 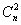 коэффициентов при различных взаимодействиях двух факторов bij,
коэффициентов при различных взаимодействиях двух факторов bij,  коэффициентов тройных взаимодействий факторов bijk, …..,
коэффициентов тройных взаимодействий факторов bijk, …..,  коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов
коэффициент b12…n. максимального взаимодействия факторов. Общее число определяемых коэффициентов .
. относительно центра плана. В первом столбце матрицы фигурирует фиктивная переменная Х0, необходимая для вычисления свободного члена уравнения регрессии b0. Большее значение переменной согласно принятой программе эксперимента соответствует верхнему уровню и обозначается (+1), меньшее значение – соответствует нижнему уровню и обозначается (-1).
относительно центра плана. В первом столбце матрицы фигурирует фиктивная переменная Х0, необходимая для вычисления свободного члена уравнения регрессии b0. Большее значение переменной согласно принятой программе эксперимента соответствует верхнему уровню и обозначается (+1), меньшее значение – соответствует нижнему уровню и обозначается (-1). .
.



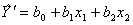
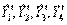 по нему.
по нему. ;
; ;
; .
. .
.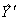 . Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида
. Если точность сокращенного полинома не удовлетворяет, то по тем же результатам опытов можно сформировать более полный полином вида .
.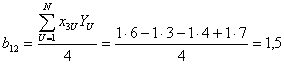 .
. .
. ). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана (
). Поверхность, построенная по полученному полиному, проходит точно через четыре точки плана ( =0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1 =0, х2 =0), предсказанные и действительные значения, могут не совпадать (
=0), по которым определены коэффициенты. Однако в других точках области определения функции, например в центре плана (точка 5 в плане, х1 =0, х2 =0), предсказанные и действительные значения, могут не совпадать ( =3).
=3).


