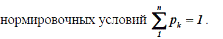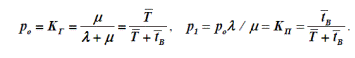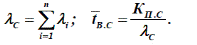Математические модели надежности систем

ЭЛЕКТРОЭНЕРГЕТИКИ, ОСНОВАННЫЕ НА МАРКОВСКИХ ПРОЦЕССАХОСОБЕННОСТИ СЛУЧАЙНЫХ ПРОЦЕССОВ, ИСПОЛЬЗУЕМЫХ ПРИ

РЕШЕНИИ ЗАДАЧ НАДЕЖНОСТИ

План лекции

1. Особенности случайных процессов, используемых при решении задач надежности

2. Схема полного отказа относительно узла

3. Схема одного отказа

4.Схема двух отказов

Краткое содержание лекции

Процессы смены состояний систем электроэнергетики и изменениятребуемой мощности во времени представляют собой случайные процессы,природа которых различна. Число дискретных состояний в сложной схемеисключительно велико, поэтому на практике невозможно оценить надежность,не разработав эффективного метода сокращения числа рассматриваемыхсостояний до приемлемого уровня.

Последствия отказов функционирования отдельных элементов в сложныхсистемах могут быть различными. Отказ элемента или группы в одном случаеможет приводить к ограничению потребляемой мощности, в другом – кполному прекращению электроснабжения потребителей одного или несколькихузлов нагрузки. В первом случае отказ частичный, во втором – полный.Конечной целью расчета надежности является количественная оценкакомплексных показателей надежности относительно подстанций, станций,узлов нагрузки или системы в целом и разработка на основе полученныхрезультатов мероприятий по их улучшению.Недоотпущенная электроэнергия зависит от состояния элементовсистемы в каждый момент времени и от спроса мощности в узлах, поэтому каксмену состояний системы, так и недоотпущенную электроэнергию следуетмоделировать случайными процессами.Процессы смены состояний электроэнергетической системы описываютсяМарковскими случайными процессами.

Процесс называется Марковским, если для каждого момента временивероятность любого состояния элемента или системы в будущем зависит отсостояния в настоящий момент и не зависит от того, каким образом элементпришел в это состояние. Законы распределения мощности в зависимости отсостава потребителей могут меняться от полимодального до нормального. Врасчетах надежности в основном принимают нормальный закон распределенияпотребляемой мощности в узлах нагрузки.В виду того, что для системы число состояний равно 2п, где п – числоэлементов, необходимо ее эквивалентирование. Например, для системы из 100элементов в общем случае число состояний равно 1,26⋅10³⁰.

Основным приемом, используемым для решения задач надежности,является исключение из рассмотрения маловероятных событий и сокращениечисла состояний до приемлемого уровня. Осуществить это можно следующимиспособами:

1) Выделение состояний, соответствующих полному отказу системы илиполностью работоспособному состоянию. Эту схему назовем схемой полногоотказа относительно узла;

2) Объединение в одно состояние ксостоянию системы, т.е. возможноэквивалентирование цепей, состоящих из последовательно соединенныхэлементов (в смысле надежности), в один эквивалентный элемент. Этот способможно распространить также на отказ при каскадной аварии в энергосистеме,когда отказ одного элемента приводит с некоторой вероятностью, неравнойединице, к каскадному отключению ряда элементов и массовому нарушениюпитания потребителей. При этом рассматривается одно состояние сК_Кэлементами, отключенными при каскадной аварии, хотя остальные (п–К_К)элементов работоспособны. Эту схему назовем схемой одного состояния.

3) Рассмотрение (п+1) состояний системы, из которых п соответствуютотказу одного j-го расчетного элемента системы и каждому j-му состояниюсоответствует определенный недоотпуск электроэнергии. Эту схему назовемсхемой одного отказа.

4) Рассмотрение состояний системы, когда два элемента находятся всостоянии отказа. Эта схема называется схемой двух отказов.

5) Неучет вероятности других состояний с числом отказавших элементовболее трех в практических расчетах как маловероятных, так как времянахождения системы в этих состояниях считается пренебрежимо малым.Из данного рассмотрения следует, что все случаи отказа системы(частичного и полного) приближенно можно свести к трем основным:

а) Отказ и восстановление одного элемента

б) Отказ и восстановление одного элемента из п элементов при (п–1)работоспособных (схема одного отказа и схема одного состояния). Эти схемыприводятся к схемам с последовательным соединением элементов, но сразными недоотпусками электроэнергии.

в) Отказ и восстановление двух резервирующих друг друга элементов привыполнении ими функций в системе (схема двух отказов). Эта схемаприводится к схеме параллельного соединения двух элементов (в смысленадежности).

 

ПРОЦЕССЫ ОТКАЗОВ И ВОССТАНОВЛЕНИЙ ОДНОЭЛЕМЕНТНОЙ СХЕМЫ. НЕРЕЗЕРВИРОВАННАЯ СХЕМА, СОСТОЯЩАЯ ИЗ NЭЛЕМЕНТОВ.

ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ В СМЫСЛЕ

НАДЕЖНОСТИ

План лекции

1. Процессы отказов и восстановлений одноэлементной схемы

2. Нерезервированная схема, состоящая из nэлементов

3. Последовательное соединение элементов в смысле надежности

Краткое содержание лекции

Марковский случайный процесс можно описать обыкновеннымидифференциальными уравнениями, в которых неизвестными являютсявероятности состояний.Элемент или установка без резервирования может находиться в двухсостояниях:

0 – работоспособное;

1 – отказ.

Определим соответствующие вероятности состояний элемента впроизвольный момент времени t при различных начальных условиях (н.у.).Процесс изменения состояний рассматриваемого элемента можнопроиллюстрировать с помощью графа переходов из состояния в состояние (см.рис. 14.1):

Рисунок 14.1. Граф перехода из состояния в состояние для одноэлементной схемы

Вершинам графа соответствуют состояния элемента: 0;1, ребрам –возможные переходы из одного состояния в другое.

Из рабочего состояния элемент перешел в состояние отказа завремя t по ребру →λ dt (переход), или из состояния отказа за время t элемент перешел в состояние работы по ребру ←μ dt (переход).За время t не произошло изменения состояния, т.е. из работы элементперешел в работу: ребро 1 −λ dt, аналогично – из отказа в отказ, т.е. элемент невосстановился за время t: ребро 1 − μ dt.

Если имеется направленный граф состояний, то системудифференциальных уравненийдля вероятностей состояний можно записать,пользуясь следующим правилом:

В левой части каждого уравнения стоит производная dp (t) / dt синдексом 0 или 1 в зависимости от рассматриваемого состояния, а в правой –столько составляющих, сколько ребер связано непосредственно сданнымсостоянием. Если ребро оканчивается в данном состоянии, то составляющаяимеет знак «+»; если начинается из данного состояния, то составляющаяимеет знак «–». Каждая составляющая равна произведению интенсивности

потока событий (λ или μ), переводящего элемент или систему по данномуребру в другое состояние, на вероятность того состояния, из которогоначинается ребро.

Согласно данному правилу состояние работы описывается уравнением:

Состояние отказа описывается уравнением:

Полученную систему дифференциальных уравнений можно использоватьдля определения:

- вероятностей безотказной работы систем;

- вероятностей отказа;

- коэффициента оперативной готовности;

- вероятности нахождения в ремонте нескольких элементов;

- среднего времени пребывания системы в любом состоянии;

- интенсивности отказов системы с учетом н.у. (состояний элементов).

Решение системы уравнений, описывающих состояние одного элемента,при начальных условиях: элемент в работе, т.е. po (0) = 1; p₁ (0) = 0, имеетвид:

Если в начальный момент времени элемент находится в состоянии отказа,т.е.

Для стационарного состояния (t →∞) вероятность работы элементаравна стационарному коэффициенту готовности Г K, а вероятность отказа –стационарному коэффициенту вынужденного простоя, П K:

Продолжительность времени, в течение которого вероятности p _o (t) и p ₁ (t) достигают установившегося значения, зависит от показателя степени (λ + μ), т.е. от коэффициента затухания экспоненты.

Стационарные коэффициенты готовности K _Г и отказа K _П можноинтерпретировать, как среднюю вероятность застать систему соответственно врабочем состоянии или состоянии отказа.Обычно в расчетах показателей надежности для достаточно длинныхинтервалов времени без большой погрешности вероятностисостояний системы можно определять по установившимся среднимвероятностям:

Такого рода состояния сточки зрения надежности называются предельными. Вероятности установившихся состояний находятся просто из системыалгебраических уравнений, полученных из дифференциальных уравненийприравниванием

В этом случае система уравнений для элемента с двумя состояниямибудет иметь вид:

Таким образом, получился тот же результат, что и при анализепредельных состояний с помощью дифференциальных уравнений.

Система, состоящая из п последовательно соединенных элементов,причем восстанавливаемых, отказывает в тех случаях, когда любой изэлементов выйдет из строя. Система из п однородных последовательносоединенных элементов имеет два состояния (см рис. 14.2):

Рисунок 14.2. Граф переходов из состояния в состояние для схемы споследовательно соединенными элементами

0 – все элементы в безотказном состоянии;

1 – один из элементов, а, следовательно, и система, всостоянии отказа.

Тогда система дифференциальных уравнений будет иметь вид:

При начальных условиях: система в работе, т.е. p_o (0) = 1, p₁(0) = 0,решение системы дифференциальных уравнений имеет вид:

При начальных условиях: система в состоянии отказа, т.е. p₀(0) = 0, p₁(0) = 1 решение системы дифференциальных уравнений следующее:

Если система неоднородна, то в вышеприведенных формулах вместо n, т.е. числа элементов с одинаковыми показателями надежности, нужно ставитьзнак Σ.

Для стационарного состояния (t →∞) коэффициенты готовности K _Г.С. ивынужденного простоя системы K _П.С. имеют вид:

Выразим коэффициент готовности системы через коэффициентыготовности ее элементов при условии, что элементы системы имеютодинаковые показатели надежности:

Аналогично для коэффициента вынужденного простоя системы при томже условии:

Если элементы системы имеют различные показатели надежности, тосистема может находиться в различных по продолжительности состоянияхотказа.

Тогда

При небольшом значении числа элементов в рассматриваемой системе впрактических расчетах для системы с высоконадежными элементами можнопользоваться приближенными формулами

Для такой схемы эквивалентная интенсивность отказа и эквивалентноесреднее время восстановления можно определять так: