
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Надежность системы, состоящей из резервируемыхСодержание книги
Поиск на нашем сайте ВОССТАНАВЛИВАЕМЫХ ЭЛЕМЕНТОВ. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ В СМЫСЛЕ НАДЕЖНОСТИ. СОСТОЯНИЯ ПОЛНОГО ОТКАЗА И БЕЗОТКАЗНОЙ РАБОТЫ СХЕМ План лекции 1. Надежность системы, состоящей из резервируемых восстанавливаемых элементов 2. Параллельное соединение элементов в смысле надежности 3. Расчет показателей надежности с учетом ремонтных состояний и преднамеренных отключений элементов 4. Состояния полного отказа и безотказной работы схем Краткое содержание лекции Для не резервированных систем в процессе работы не удаетсявосстанавливать отказавшие элементы, их необходимо отключать. При этомсокращение времени переключений и восстановления отказавших элементовповышает готовность системы, но практически не влияет на ее безотказность.Если в системе есть резервирование, то восстановление являетсяэффективным средством повышения надежности. Дублированием функцийвосстанавливаемых элементов и сокращением времени восстановления можнодобиться сколь угодно высокой степени надежности системы. Целью расчета резервированной системы является определениевероятности непрерывной безотказной работы, среднего времени безотказнойработы и интенсивности или параметра потока отказов (λ или ω),стационарного значения коэффициента вынужденного простоя системы дляоценки недоотпуска электроэнергии в состоянии с двумя отказавшимиэлементами (схема двух отказов). Особенности резервированных систем с восстановлением целесообразнорассмотреть на примере двух взаиморезервирующих элементов 1 и 2, например,параллельные линии электропередачи, взаиморезервирующие силовыетрансформаторы на подстанции и т.д. Предполагается, что во время восстановления в элементах не могутвозникнуть вторичные отказы. Вероятность отказа при вводе резерва равнанулю. Такая система может находиться в четырех состояниях: 1. Система работоспособна, (оба элемента в работе); 2. Система работоспособна, но первый элемент отказал; 3. Система работоспособна, но второй элемент отказал; 4. Система не работоспособна (оба элемента в состоянии отказа). Граф переходов из состояния в состояние будет иметь вид (см. рис. 15.1):
Рисунок 15.1. Граф переходов из состояния в состояние для двух взаиморезервируемых элементов При интерпретации ≪на схему двух отказов≫ состояния 2, 3 означаютпереход системы в состояние, соответствующее схеме ≪одного отказа≫. Приэтом предполагается, что резерв нагруженный, а элементы могутремонтироваться как по одному, так и одновременно.Система дифференциальных уравнений, описывающая вероятностисостояний во времени и полученная на основании вышеприведенного правилапо составлению таких систем, имеет следующий вид:
Как известно из теории дифференциальных уравнений, в общем виде решение системы дифференциальных уравнений записывается так:
где k = 1,2,...,N - число состояний системы;
Функции готовности и вынужденного простоя системы имеют вид:
Для стационарного состояния (при t →∞) средние вероятности состояний следующие:
откуда можно найти параметр потока отказов системы из двух взаиморезервирующих друг друга элементов:
Следовательно, параметр потока отказов системы, состоящей из двух резервирующих руг друга элементов, равен сумме произведений параметра потока отказов первого на среднюю вероятность отказа второго и параметра потока отказов второго на среднюю вероятность отказа первого элемента. Этот вывод имеет важное практическое значение, а слагаемые
Система из n взаиморезервирующих элементов Для определения параметра потока отказов системы из n взаиморезервирующих элементов необходимо рассмотреть столько слагаемых, сколько элементов входит в систему, тогда
Если показатели надежности элементов одинаковы, то:
Например, для двух взаиморезервирующих элементов с одинаковыми показателями надежности:
Для трех взаиморезервирующих элементов с разными показателями надежности:
Т. о., можно выработать общее правило оценки надежности системылюбой сложности с произвольным соединением элементов, если для системыопределяются показатели полного отказа. Параметр потока отказов системы, состоящей из независимыхвосстанавливаемых элементов, равен сумме произведений параметрапотока отказов каждого элемента на среднюю вероятность отказа частисистемы, оставшейся после исключения этого элемента. При этом еслиотказ рассматриваемого элемента приводит к отказу системы, товероятность отказа оставшейся части принимается равный единице(например, последовательное в смысле надежности соединение элементов). Расчет показателей надежности с учетом ремонтных состоянийи преднамеренных отключений элементов Проведение профилактических и капитальных ремонтов оборудованиясистем электроэнергетики предусматривает отключение элементов, изменениесхем коммутации, что приводит к изменению их уровня надежности в этотпериод времени. Преднамеренные отключения элементов производятся нетолько с целью ремонта, но и по заявкам других организаций. Частота ипродолжительность преднамеренных отключений элементов в общем случаезависят от случайных факторов и задаются параметром потока преднамеренныхотключенийλ при их средней продолжительностью. В практических расчетах надежности, если система обладаетизбыточностью по надежности, то при преднамеренном отключении какого-либо элемента вся оставшаяся часть системы рассматривается как одинэквивалентный элемент. Вероятность отказа этого эквивалентного элемента вовремя преднамеренного отключения любого i-го элемента равна:
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |








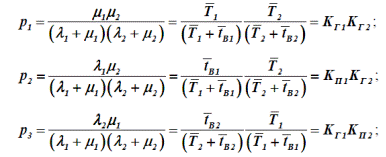


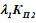 и
и 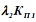 имеют смысл среднего числа отказов системы во время состояния отказасоответственно второго и первого элементов.
имеют смысл среднего числа отказов системы во время состояния отказасоответственно второго и первого элементов.


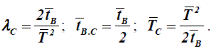
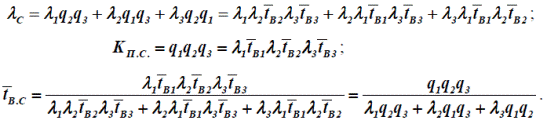
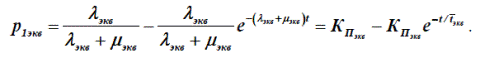


 – коэффициент, зависящий от соотношения времени восстановления резервирующего эквивалентного элемента и времени отключения i –го элемента. Этот коэффициент учитывает фактор уменьшения вероятности преднамеренного отключения одного элемента иаварийного отключения другого – резервирующего, т.е. учитываетзапрет наложения ремонта на аварию при эксплуатации.
– коэффициент, зависящий от соотношения времени восстановления резервирующего эквивалентного элемента и времени отключения i –го элемента. Этот коэффициент учитывает фактор уменьшения вероятности преднамеренного отключения одного элемента иаварийного отключения другого – резервирующего, т.е. учитываетзапрет наложения ремонта на аварию при эксплуатации.


