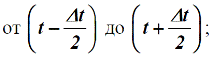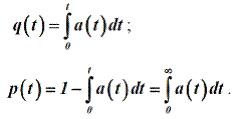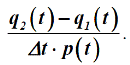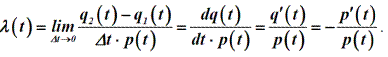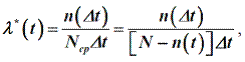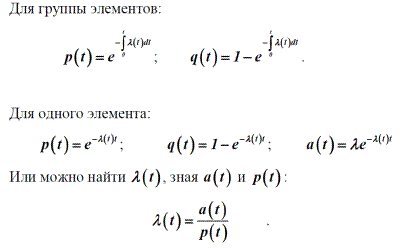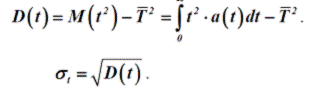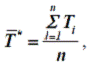Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительность понятия элемент и системав расчетах надежностиСодержание книги
Поиск на нашем сайте
В расчетах надежности объектов и систем электроэнергетики возникаетпротиворечивая ситуация: с одной стороны желание иметь наиболее точнуюмодель, адекватно описывающую процессы отказов и восстановлений, с другойстороны – стремление к простоте расчетов и обеспеченности выбраннойрасчетной модели исходными данными. В настоящее время широко распространены элементные методы расчетанадежности, которые исходят из предположения, что система состоит изсамостоятельных в смысле надежности элементов. При этом отказом элементасчитается выход его параметров (например, электрических, механических,тепловых) за пределы, при которых он перестает выполнять свои функции. Предполагается, что элемент отключается коммутационными устройствами отостальной схемы. При этом сами коммутационные устройства рассматриваютсякак самостоятельные элементы. Т.е. при расчетах такими методами неанализируются количественно функциональные зависимости междупараметрами режимов элементов, в этом их недостаток. Достоинством такихметодов является простота расчетов и возможность получения количественныхоценок надежности для современных электроустановок и систем. Понятие элемент и система относительны в расчетах надежности. Объект,считающийся системой в одной задаче, например, силовой трансформатор,состоящий из элементов: обмотки, изоляции, бака, вводов и т.д., в другойзадаче рассматривается как единый элемент, например оценка надежностиподстанции или электростанции. Или другой пример. Если исследуетсянадежность работы электрической станции, то станция представляется каксистема, а генераторы, выключатели, шины распределительных устройств (РУ),турбины и т.д. – как отдельные элементы. Если же исследуется надежностьодного генератора, то сам генератор является системой, а статор, ротор,возбудитель и т.д., т.е. его отдельные части – элементами. Деление системы на элементы зависит от характера решаемой задачи(схемный анализ, оперативное управление, конструктивное исполнение и т.д.),от точности расчета, наличия статистического материала, масштабностиобъекта в целом. Например, при определении надежности сложной системы относительноузла нагрузки группа коммутационных аппаратов, включающая разъединитель,выключатель, комплекты релейной защиты и соответствующий участок шин,представляется одним элементом. Однако, при оценке вероятности развитияаварии в сложной системе такого представления недостаточно. В этом случаетолько отказ самого выключателя является зависимым событием и состоит изтрех отказов: отказа в статическом состоянии, отказа при автоматическомотключении поврежденных смежных элементов, отказа при оперативныхпереключениях. Часто в сложных схемах двухцепные ЛЭП на одних опорах или двухцепные кабельные линии, проложенные в одной траншее, представляютсяодним элементом. В то же время, оценивая надежность самой двухцепной линии, отказы представляют совокупностью отказов одной, двух цепей иперехода отказов с одной цепи на другую. Такой подход значительно упрощает задачи анализа показателейнадежности сложных схем. Необходимо лишь правильно определять, какпредставлять объект: системой или элементом в конкретных инженерныхситуациях. Базируясь на относительности понятий элемент и система, применяютсяпоэтапные методы расчета надежности, заключающиеся в том, что на каждомпоследующем этапе сами расчетные элементы системы представляютсясистемой, с последовательным уточнением показателей надежности. С цельюуточнения показателей надежности отдельных элементов в условияхэксплуатации необходима соответствующая статистическая информация, таккак с течением времени показатели надежности начинают отличаться отзначений, полученных при заводских испытаниях. Вопросами сбора иобработки такой информации должны заниматься службы надежности. Наблюдения при нормальной эксплуатации – самый доступный источникполучения экспериментальных данных о надежности. Его недостаток –запаздывание информации, влияние субъективных факторов на объем исодержание информации. Сведения об отказах оформляются на местахоперативным и ремонтным персоналом в документы, предусмотренныестандартами и ведомственными инструкциями, собираются висследовательских и инженерных центрах и соответствующим образомобрабатываются. Посредством сбора и обработки информации о надежностиэлектроэнергетического оборудования решаются следующие задачи: - определение причин отказов; - выявление тех деталей и комплектующих, которые лимитируют надежность оборудования; - установление и корректировка нормируемых показателей надежности; - оптимизация системы планово-предупредительных ремонтов; - выявление условий и режимов эксплуатации, влияющих на надежность; - определения экономической эффективности повышения надежности. Обработка собранной статистической информации проводится согласно теории математической статистики по следующему алгоритму: Ø определение объема выборки; Ø построение гистограммы; Ø выдвижение гипотезы о законе распределения вероятностейисследуемого показателя; Ø определение точечных и интервальных оценок показателей надежности; Ø проверка статистических гипотез с помощью критериев согласия.
ПОКАЗАТЕЛИ НАДЕЖНОСТИ. ЕДИНИЧНЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ План лекции 1.Показатели надежности 2.Единичные показатели надежности Краткое содержание лекции Показателем надежности называется количественная характеристика одного или нескольких свойств, определяющих надежность объекта. Их подразделяют на единичные, характеризующие одно свойство и комплексные, характеризующие несколько свойств. Единичные показатели в основном применяются для характеристики отдельных элементов, а комплексные – для узлов нагрузки и системы в целом. Единичные показатели надежности подразделяются на показатели безотказности и восстанавливаемости. Вероятность безотказной работы p(t) – вероятность того, что в пределах заданной наработки, t, отказа не произойдет при заданных условиях работы (см. рис. 2.1):
p(t) = P(T ≥ t), где Т – время безотказной работы. Вероятность безотказной работы еще называют функцией надежности.
Рисунок 2.1 Кривая вероятности безотказной работы Помимо вероятностной существует и статистическая оценка вероятности безотказной работы:
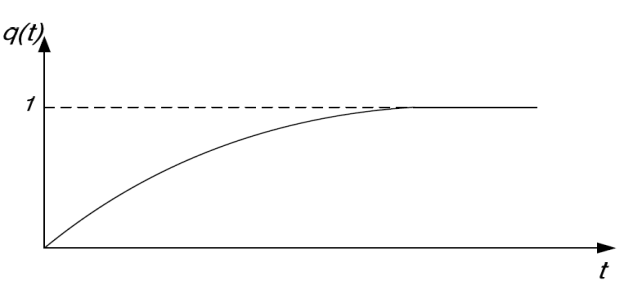
где N – число элементов в начале испытаний или объем выборки; n(t) – число отказавших элементов за время t. Из определения и графика следует, что p(t) - не возрастающая функциявремени в пределах от 0 до 1; р(0)=1, р(∞)=0. На практике часто более удобной характеристикой является вероятность отказа q(t), которая определяется как противоположное событие, т.е. это вероятность того, что в пределах заданной наработки произойдет хотя бы один отказ: q(t) = 1 − p(t); q(t) = F (t) = P(T < t). Очевидно, что p(t) + q(t) = 1. Вероятность отказа определяется также как функция распределенияслучайной величины наработки до отказа (или на отказ). Следовательно, q(t)обладает всеми свойствами интегральной функции распределения случайнойвеличины времени безотказной работы: q(0)=1, q(∞)=0. Ее ещеназывают функцией ненадежности. Кривая вероятности отказа приведена нарис. 2.2.
Рисунок 2.2 Кривая вероятности отказов
Так же как и для вероятности безотказной работы применяютстатистическую оценку вероятности отказа:
Частота отказов a(t) - дифференциальная функция распределения илиплотность распределения вероятностей, то есть времени работы элемента доотказа – отношение числа отказавших элементов в единицу времени кпервоначальному числу испытуемых элементов.Вероятностное определение a(t) следующее:
Ее статистическая оценка определяется как:
где
N – число элементов (образцов), участвующих в испытании.Между частотой отказов, вероятностью отказов и вероятностьюбезотказной работы при любом законе распределения времени возникновенияотказов существуют однозначные зависимости:
Отсюда, зная частоту отказов, можно вычислить вероятность безотказнойработы и ее характеристики.Интенсивность отказов λ (t) – скорость изменения вероятностибезотказной работы или условная вероятность того, что в промежуток времениt произойдет отказ, при условии, что до этого он не произошел:
С вероятностной точки зрения отказ в промежутке времени
Тогда интенсивность отказа определится как:
Согласно статистической оценке интенсивность отказов, λ (t) -отношение числа отказавших элементов в единицу времени к среднему числу элементов, работающих в данный отрезок времени:
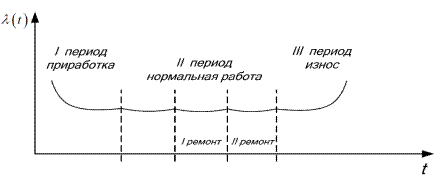
где Ncp – среднее число работающих элементов в рассматриваемый отрезок времени; n(t) – число отказавших элементов к рассматриваемому промежутку времени. Изменение интенсивности отказа во времени показано на рис.2.3. Графикзависимости интенсивности отказа от времени обычно называют характеристикой жизни объекта.
Рисунок 2.3. Типичная кривая изменения интенсивности отказов во времени Из кривой зависимости интенсивности отказов от времени видно, что весь период работы элемента условно делится на три части: приработка, нормальная работа, износ. Приработка Приработочные отказы являются, как правило, результатом наличия в элементе дефектов или дефектных деталей, надежность которых значительно ниже требуемого уровня. Кроме того, к отказам в этот период могут приводить ошибки при сборке или монтаже, а также недостаточная освоенность элементаобслуживающим персоналом. Физическая природа таких отказов носитслучайный характер и отличается от внезапных отказов нормального периодаэксплуатации тем, что здесь отказы могут иметь место даже принезначительных нагрузках («выжигание дефектных деталей»).Снижение величины интенсивности отказов изделия или всего объектапри постоянном значении этого параметра для каждого из элементов вотдельности как раз и объясняется «выжиганием» слабых звеньев и их заменойболее надежными. Чем круче кривая на первом участке, тем лучше: меньшедефектных элементов остается в изделии за более короткий срок к моментуначала нормальной эксплуатации. Нормальная работа Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили, т.е. в этот период могут быть только внезапные отказы нормально работающих элементов, наработка на отказ которых очень велика. Сохранение уровняинтенсивности отказов на этом этапе характеризуется тем, что отказавшийэлемент заменяется таким же с той же вероятностью отказа, а не лучшим, какэто происходило на этапе приработки. В период нормальной работыинтенсивность отказа постоянна, что достигается диагностикой ипредупредительными ремонтами. Износ Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы, обусловленные старением объекта. Наступаеттретий период в жизни объекта – износ. Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает, а средняя частотаотказов при t →∞ равна величине, обратной времени безотказной работы.Рассмотрим связь интенсивности отказов с другими показателяминадежности. Для наиболее распространенного в расчетах надежностипоказательного или экспоненциального закона распределения, зная λ (t), можнонайти другие показатели надежности.
Время безотказной работы – случайная величина, котораяхарактеризуется математическим ожиданием T или средним временем(продолжительностью) безотказной работы и среднеквадратичнымотклонением σt. Как всякое математическое ожидание случайной величины Tопределяется зависимостью вида:
т.е. среднее время безотказной работы равно площади кривой вероятности безотказной работы. Дисперсия и среднее квадратическое отклонение времени безотказной работы соответственно равны:
Расчетное время безотказной работы
Расчетным временем безотказной работы пользуются при сравнениибезотказности работы объектов электроэнергетических систем, в особенности,если законы распределения времени безотказной работы различны. Например,для экспоненциального закона распределения:
Статистическая оценка средней продолжительности безотказной работыобъекта определяется по формуле:
где T i – время работы i-го объекта до отказа; n – начальное число объектов. Наработка на отказ – среднее время между соседними отказами при условии восстановления отказавшего элемента
где n – число отказов за время t; ti – время работы между i-м и (i+1)м отказом.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.201.46 (0.009 с.) |





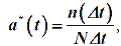
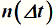 – число отказавших элементов в интервале времени t, т.е.
– число отказавших элементов в интервале времени t, т.е.