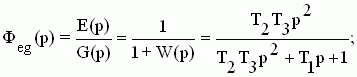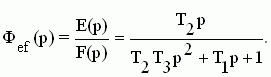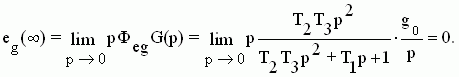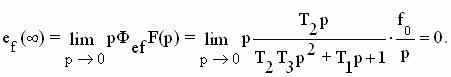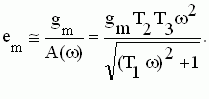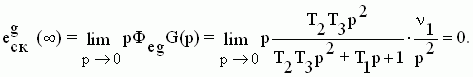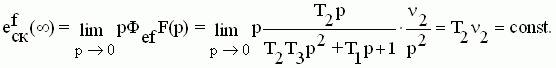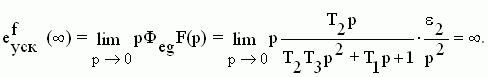Методы оценки качества переходных процессов
Похожие статьи вашей тематики
Основное преимущество частотных методов - возможность использования как расчетных, так и экспериментальных характеристик разомкнутой системы для определения качества ее после замыкания цепи обратной связи. Оценки качества процессов регулирования, вызываемых изменением структуры или параметров системы, отличаются при этом большой простотой.
Остановимся более подробно на оценке качества переходных процессов САУ по вещественной частотной характеристике. Вещественная частотная характеристика замкнутой системы Re=P(ω) позволяет приближенно оценить качество переходной характеристики и в случае необходимости построить переходный процесс. Поэтому данную характеристику часто используют при инженерных расчетах. Примерный вид вещественной частотной характеристики замкнутой системы по заданному воздействию показан на рис.5. 3.

Рис.5.3. Вещественная частотная характеристика
Интервал частот, в котором Р(ω) положительна, называется интервалом положительности ωп. Значение частоты ωсч (существенная частота), после которой кривая Р(ω) не выходит за пределы участка ± 0.1Р(0), определяет примерно границу пропускания частот исследуемой системы, если она статическая. На частоты, лежащие за пределами полосы пропускания ωсч, система практически не реагирует.
Качество переходной характеристики можно приближенно оценить по следующим признакам Р(ω).
Признак 1. Установившееся значение переходной характеристики (конечное значение)  = h( = h( ) равно начальному значению вещественной частотной характеристики Р(0). ) равно начальному значению вещественной частотной характеристики Р(0).
Признак 2. Начальное значение переходной характеристики h0=h(0) равно конечному значению вещественной частотной характеристики Р( ). ).
Признак 3. При наличии у положительной вещественной частотной характеристики максимума Рmax перерегулирование δ переходного процесса приближенно равно
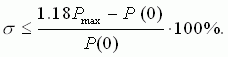
Признак 4. Не возрастающая положительная вещественная частотная характеристика с отрицательной и убывающей по абсолютной величине производной соответствует монотонному переходному процессу.
Признак 5. Если увеличить (уменьшить) масштаб Р(ω) вдоль оси абсцисс в n раз, то масштаб кривой переходного процесса вдоль оси времени уменьшится (увеличится) в тоже число раз.
Признак 6. Если изменить масштаб Р(ω) вдоль оси ординат в n раз, то и масштаб кривой переходного процесса вдоль той же оси времени изменится во столько же раз.
Признак 7. Если вещественная частотная характеристика положительна при частотах ω<ωr, то время регулирования в общем случае заведомо больше  . .
Признак 8. При положительной невозрастающей вещественной частотной характеристике перерегулирование переходного процесса не может превышать 18 %.
Признак 9. Острый пик вещественной характеристики при угловой частоте ωр свидетельствует о медленно затухающих колебаниях переходного процесса с частотой, близкой к частоте 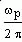 . Затухание этих колебаний тем меньше, чем острее и выше пик. . Затухание этих колебаний тем меньше, чем острее и выше пик.
Признак 10. Если Р(ω) можно представить суммой  , то и переходный процесс h(t) может быть представлен суммой составляющих , то и переходный процесс h(t) может быть представлен суммой составляющих  , где , где 
Заметим, что лишь некоторые из приведенных признаков смогут быть строго доказаны, остальные же получены при рассмотрении решений большого числа типичных примеров или выведены для частных, но весьма распространенных видов вещественных характеристик. Поэтому использование этих признаков требует осторожности и проверки результатов исследования построением переходных процессов.
Рассмотрим связь показателей качества работы в замкнутой системе с ЛЧХ разомкнутой САУ. На рис.5.4 показаны типовые л.а.х. и л.ф.х. разомкнутой системы. Параметры переходного процесса (рис.5.1) и ЛЧХ связаны между собой следующими соотношениями:

Из формул видно, что быстродействие САУ прямо пропорционально частоте среза ωcp, а колебательность обратно пропорциональна запасу устойчивости по фазе φзап. Следует отметить, что приведенные формулы являются приближенными (погрешность может составлять от 20 до 25 %), но на этапе предварительного анализа их использование может быть полезным.
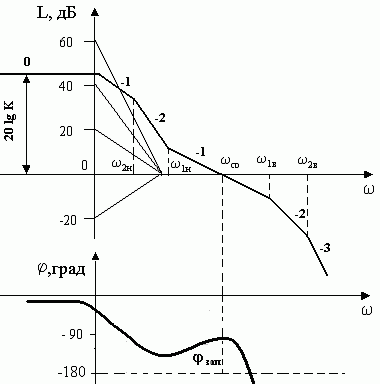
Рис.5.4. Типовые ЛЧХ разомкнутой САУ
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
| Корневые критерии качества
|  
|  
|  
| Отметим некоторые особенности применения корневых критериев качества переходных процессов. Эти критерии основаны на оценке качества переходных процессов по расположению и значению полюсов и нулей передаточной функции системы, т. е. по расположению и значению корней ее знаменателя и числителя на комплексной плоскости корней. Отметим, что если при исследовании устойчивости нас интересовали только полюсы передаточной функции, т. е. корни характеристического уравнения, то при исследовании качества необходимо учитывать и нули передаточной функции. Лишь в частном случае, когда передаточная функция системы не имеет нулей, качество переходных процессов определяется только коэффициентами характеристического уравнения.
Система будет склонна к колебаниям, если имеются комплексные корни вида -α±jβ где: α - коэффициент затухания; β - круговая частота колебаний. Наибольший из углов φ, образованных отрицательной действительной полуосью и лучами, проведенными из начала координат через мнимые части корней, характеризует колебательность системы. Котангенс этого угла m=ctg(α/β) называется коэффициентом затухания колебаний или степенью устойчивости (рис.5.5).

Рис.5.5. Расположение корней характеристического уравнения
Для оценки быстродействия может использоваться понятие степени быстродействия (иногда называют степенью устойчивости) η - это абсолютное значение вещественной части ближайшего к мнимой оси корня. Т.е. если этот корень -α±jβ, то η равна коэффициенту затухания α.
Поскольку корни характеристического уравнения, расположенные ближе к мнимой оси, т. е. имеющие наименьшую по абсолютной величине вещественную часть, дают составляющие переходной характеристики, которые затухают наиболее медленно, то по степени устойчивости можно приближенно определить время регулирования:
tп=3/η - если ближайший к мнимой оси корень вещественный;
tп<3/η - если ближайшей к мнимой оси является пара комплексных сопряженных корней.
Значение степени колебательности m позволяет найти приближенное значение перерегулирования переходной характеристики (в %):
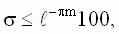
если ближе к мнимой оси расположена пара комплексных сопряженных корней.
Если требуется, чтобы САУ имела определенные значения степени устойчивости и коэффициент затухания m, необходимо, чтобы все корни характеристического уравнения этой системы располагались внутри заштрихованной области (рис.5.5). Следует однако помнить, что для определения более точно качества переходного процесса при единичном скачке задающего воздействия существенны не только корни характеристического уравнения, т.е. полюса, но также и нули передаточной функции замкнутой системы.
Для устойчивой системы, не имеющей нулей, можно пользоваться некоторой обобщенной оценкой, называемой среднегеометрическим корнем Ω, который равен
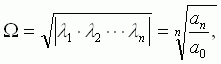
где аn и a0 соответственно свободный член и коэффициент при старшей степени оператора р характеристического уравнения; λi - корни.
Для статических САУ аn=1+К, а для астатических аn=К, а0=T1 T2 …Tn, следовательно увеличение К приводит к увеличению Ω, поэтому на основании теоремы подобия увеличение Ω приводит к пропорциональному смещению корней. Таким образом, вид переходного процесса меняться не будет, но быстродействие изменится, т.е. параметр Ω является мерой, характеризующей быстроту протекания переходных процессов, так как время регулирования системы будет тем меньше, чем больше Ω. Зная значения нулей и полюсов передаточной функции можно построить и исследовать корневой годограф (примером является диаграмма Вышнеградского). Однако трудоемкость построения корневых годографов сложных систем ограничивает применение корневых методов в инженерной практике.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
| Интегральные оценки качества
|  
|  
|  
| Широкое распространение среди косвенных методов исследования качества процессов регулирования получили интегральные оценки. Это оценки качества переходной характеристики, а именно: быстроты затухания ее колебаний и величины отклонения регулируемого параметра от установившегося значения. Рассмотрим наиболее употребительные интегральные оценки.
Линейная интегральная оценка численно равна площади, ограниченной ошибкой регулирования е(t) = hуст - h(t). Определяется она выражением
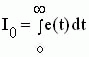
Если известна передаточная функция САУ и на вход системы поступило единичное ступенчатое воздействие, то значение I0 находится весьма просто
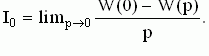
Линейную интегральную оценку применяют только для монотонных переходных процессов (рис. 5.2.(1)), так как при колебательном переходном процессе (рис.5.2.(3)) ошибка в определении качества может быть недопустимой. Для улучшения свойств предыдущего критерия используют интеграл от модуля ошибки
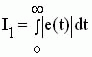
Ограниченность применения данной оценки заключается в трудоемкости ее вычисления.
Недостатки двух первых интегральных оценок преодолеваются квадратичной интегральной оценкой (формула Рэлея)
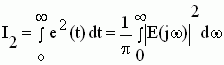
На рис.5.6 представлена геометрическая интерпретация квадратичной интегральной оценки качества, численно равная площади, заключенной между осью времени и квадратом динамической ошибки регулирования e2(t).
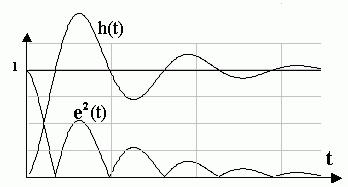
Этот интеграл находится также по виду передаточной функции замкнутой САУ. Целесообразность же ее применения обусловлена тем, что существуют готовые формулы для расчета численных значений I2.
Следует однако заметить, что минимизация оценки I2 приближает кривую переходного процесса к 1(t), что, в свою очередь, вызывает значительное увеличение скорости отработки сигнала в начальный момент времени. Чтобы получить быстро затухающий и достаточно плавный процесс, вводят улучшенные квадратичные интегральные оценки качества, например
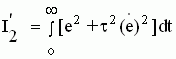
где τ назначается в соответствии с заданием желаемых свойств переходного процесса. В этом случает предельной переходной характеристикой будет экспонента е+τ  =0 с желаемой постоянной времени τ, получившая название экстремаль.Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи. =0 с желаемой постоянной времени τ, получившая название экстремаль.Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обу
Точность работы САУ
| Передаточные функции ошибок
|  
|  
|  
| Оценка точности работы САУ подразумевает нахождение величины установившейся ошибки в различных типовых (детерминированных) режимах. Принято типовые режимы исследовать следующих видов, т.е. при подаче на систему воздействий:
1. ступенчатое воздействие 1(t)-->1/p;
2. движение с постоянной скоростью 1(t)t-->1/p2;
3. движение с постоянным ускорением 1(t)(t2)/2-->1/p3;
4. движение по гармоническому закону 1(t)-->sin(ωt) /(p2 + ω2).
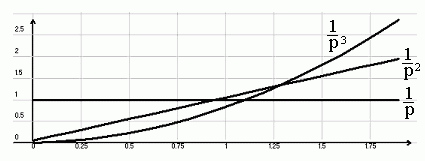
Рис.5.7. Типовые воздействия
На рис.5.8 представлена обобщенная структурная схема САУ с одним входом и одним возмущающим воздействием, позволяющая сформулировать правило определения порядка астатизма по тому или иному воздействию

Рис. 5.8. Структурная схема системы управления
где: WR(p) - передаточная функция регулятора; Wo(p) - передаточная функция объекта управления; G(p), F(p), U(p), Е(p), Y(p) - соответственно изображения по Лапласу задающего и возмущающего воздействий, рассогласования (ошибки регулирования) и управляемой величины.
Изображение ошибки регулирования имеет вид: 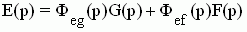
При f(t)=0 -->  - передаточная функция замкнутой системы по ошибке относительно задающего воздействия. - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
При g(t)=0 -->  - передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия. - передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.
Изображение выходной переменной имеет вид: 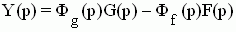 . .
При f(t)=0 -->  - передаточная функция замкнутой системы по задающему воздействию. - передаточная функция замкнутой системы по задающему воздействию.
При g(t)=0 -->  - передаточная функция замкнутой системы по возмущающему воздействию. - передаточная функция замкнутой системы по возмущающему воздействию.
Таким образом, четверка передаточных функций Фg(p), Фf(p), Феg(p), Феf(p) полностью определяет замкнутую систему управления. Передаточная функция разомкнутой системы имеет вид:  . .
Передаточная функция разомкнутой системы W(p) имеет большое значение в классической теории управления, так как методы анализа и синтеза систем основаны на ее использовании.
Найдем передаточные функцию замкнутой системы.
1. Передаточная функция замкнутой САУ по управляющему воздействию при f(t)=0
 . .
2. Передаточная функция замкнутой САУ по ошибке от управляющего воздействия при f(t)=0
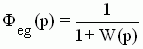
3. Передаточная функция замкнутой САУ по возмущающему воздействию при g(t)=0 и по ошибке от этого воздействия для САУ на рис.5.8 имеет вид
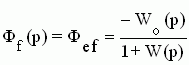
Таким образом, передаточные функции замкнутой системы определяются передаточной функцией разомкнутой системы.
Из вышеприведенного вытекает следующее:
1. D(p)=1+W(p)=0 - характеристическое уравнение замкнутой САУ;
2.  ; ;
3. 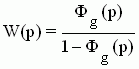 ; 4. ; 4.  . .
© В.Н. Бакаев, Вологда 2004. Раз
Для оценки точности системы определяется установившаяся ошибка, которая может быть получена с помощью теоремы операционного исчисления о конечном значении функции:

где  - установившееся значение ошибки от задающего воздействия; - установившееся значение ошибки от задающего воздействия;
 - установившееся значение ошибки от возмущающего воздействия. - установившееся значение ошибки от возмущающего воздействия.
Изображение ошибки от задающего воздействия имеет вид  , ,
где Φeg(p) - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
Для получения коэффициентов ошибок передаточная функция Φeg(p) раскладывается в степенной ряд
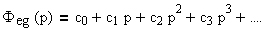
Коэффициенты ci этого ряда называются коэффициентами ошибок и определяются из выражения
 при i=0, 1, 2, 3,... при i=0, 1, 2, 3,...
Коэффициенты c0, c1 и c2 называются соответственно коэффициентами позиционной ошибки, скоростной ошибки и ошибки от ускорения.
Выражение для изображения ошибки от задающего воздействия примет вид

Перейдя к оригиналу, выразим установившуюся ошибку через коэффициенты ошибок, задающее воздействие и его производные:
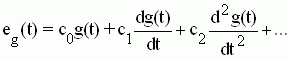
Аналогично можно ввести понятие коэффициентов ошибок по возмущающему воздействию.
Рассмотрим ошибки регулирования для различных систем и различных типовых управляющих воздействий. Аналогичные результаты можно получить и для различных возмущающих воздействий с учетом порядка астатизма, так как САУ с астатизмом по управляющему воздействию может быть статической по возмущению.
Итак, если взять статическую САУ, то у нее в области низких частот передаточная функция разомкнутой системы W(p) 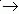 K при p K при p 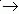 0. Подадим на вход замкнутой системы управляющее воздействие, представленное рядом Тейлора: 0. Подадим на вход замкнутой системы управляющее воздействие, представленное рядом Тейлора:
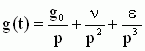 , где g0 - постоянная составляющая; ν - скоростная составляющая; ε - составляющая ускорения. Тогда установившееся значение ошибки управления будет , где g0 - постоянная составляющая; ν - скоростная составляющая; ε - составляющая ускорения. Тогда установившееся значение ошибки управления будет
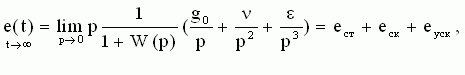
где:  = const - статическая ошибка; eск= = const - статическая ошибка; eск=  - скоростная ошибка; eуск= - скоростная ошибка; eуск=  - ошибка по ускорению. - ошибка по ускорению.
Т.е. в статических системах ошибка, вызванная заданием, равным константе, так же константа, но меньшая в (1+К) раз, а ошибки от заданий, меняющихся с постоянной скоростью ν или ускорением ε, нарастают до бесконечности.
Если САУ обладает астатизмом первого порядка, то передаточная функция разомкнутой системы в области низких частот W(p) 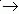 Kν/p при p Kν/p при p 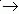 0. Тогда установившаяся ошибка управления будет 0. Тогда установившаяся ошибка управления будет
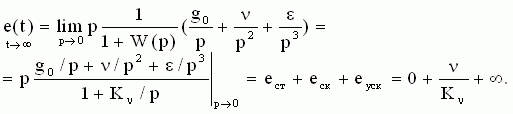
Т.е. в астатической системе первого порядка ошибка от задания, равного константе, равна нулю, ошибка от задания, меняющегося с постоянной скоростью, равна eск=ν/Kν, а ошибка от задания, меняющегося с постоянным ускорением, нарастает до бесконечности.
Если САУ обладает астатизмом второго порядка, то в области низких частот передаточная функция разомкнутой системы W(p) 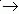 Kε/p2 при p Kε/p2 при p 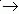 0. 0.
Тогда установившаяся ошибка управления будет
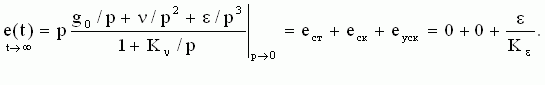
Т.е. в астатической системе второго порядка ошибка от задания, равного константе, равна нулю, ошибка от задания, меняющегося с постоянной скоростью также равна нулю, а ошибка от задания, меняющегося с постоянным ускорением, равна eуск=ε/Kε.
Анализ показывает, что точность работы САУ с астатизмом зависит от величин, называемых добротностью по скорости Kν и ускорению Kε. На рис.5.9 приведены л.а.х. двух систем с астатизмом первого и второго порядка, по которым можно определить значения добротностей.

Рис.5.9. ЛЧХ астатических САУ: а - астатическая 1-го порядка;
б - астатическая 2-го порядка.
Если на вход САУ подать гармоническое воздействие  , то установившаяся ошибка также будет изменяется по гармоническому закону с той же частотой: , то установившаяся ошибка также будет изменяется по гармоническому закону с той же частотой:
 . .
Точность системы в этом режиме оценивается по величине амплитуды ошибки, которую можно определить из амплитудно-частотной характеристики или модуля передаточной функции замкнутой системы. Следовательно
 . .
Для реальных систем в большинстве своем справедливо |W(jω)| >>1. В связи с этим единицей в знаменателе, приведенной выше формулы, можно пренебречь. Тогда амплитуда ошибки
 , ,
где A(ω) - модуль частотной передаточной функции разомкнутой системы.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучени
| Определение порядка астатизма
|  
|  
|  
| Чтобы сформулировать правило для определения порядка астатизма по тому или иному воздействию, рассмотрим пример САУ с одним управляющим и одним возмущающим воздействием. Для примера рис.5.10. возьмем ПИ - регулятор и нейтральный объект.
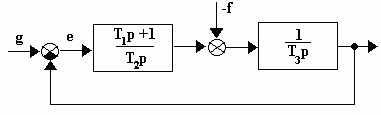
Рис.5.10. Структурная схема САУ
Найдем установившиеся ошибки системы при различных внешних воздействиях.
Передаточная функция замкнутой САУ по ошибке:
- от управляющего воздействия
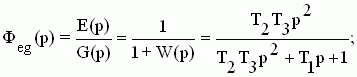
- от возмущающего воздействия
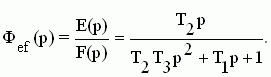
1. Возьмем g(t)=g0*1(t), f(t)=f0*1(t). Тогда G(р)= g0/p, F(p)= f0/p.
Установившаяся ошибка от управляющего воздействия:
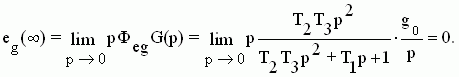
Установившаяся ошибка от возмущающего воздействия:
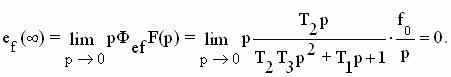
2.  , f(t)=0. Амплитуда ошибки , f(t)=0. Амплитуда ошибки
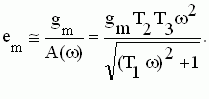
3. Подадим сигналы управления и возмущения, линейно нарастающие с постоянной скоростью, изображения которых G(р)=ν1/p2, F(p)=ν2/p2.
Скоростная установившаяся ошибка от управляющего воздействия:
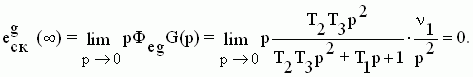
Скоростная установившаяся ошибка от возмущающего воздействия:
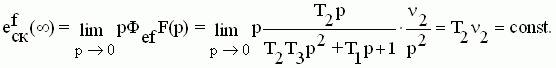
4. Подадим сигналы управления и возмущения, нарастающие с постоянным ускорением, изображения которых G(р)=ε1/p3, F(p)=ε2/p3.
Ошибка по ускорению от управляющего воздействия:
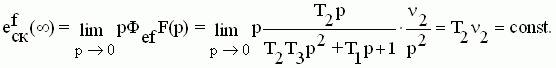
Ошибка по ускорению от возмущающего воздействия:
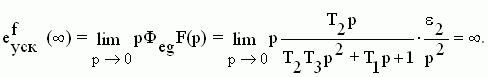
На основании приведенного выше анализа астатизма по управляющему и возмущающему воздействиям можно заключить: порядок астатизма по тому или иному воздействию определяется количеством интегрирующих звеньев в цепи обратной связи между интересующим воздействием и ошибкой управления. Таким образом, астатизм САУ по управляющему воздействию равен 2 (два интегрирующих звена в цепи обратной связи - между ошибкой е(t) и управляющим воздействием g(t)), а по возмущающему воздействию астатизм равен 1 (одно интегрирующее звено в цепи обратной связи - между ошибкой е(t) и возмущающим воздействием f(t)). Поэтому по управлению εст=εск=0 (две первые ошибки), а по возмущению только εст=0 (одна первая ошибка).
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обуче
| Методы повышения точности работы САУ
|  
|  
|  
| Повышение точности работы САУ возможно с помощью изменения ее структуры или изменения параметров. Общими методами повышения точности являются:
1. Увеличение коэффициента усиления К разомкнутой системы (регулирование по отклонению с использованием П - регулятора).
2. Повышение порядка астатизма (регулирование по интегралу от ошибки с использованием ПИ - регулятора).
3. Применение регулирования по производным от ошибки (с применением ПД - регуляторов).
4. Использование комбинированного управления.
5. Введение неединичных обратных связей.
При регулировании по отклонению ошибка тем меньше, чем больше К. Метод эффективен, широко применяется, но в системах высокого порядка сказывается противоречие между требованием точности и требованием устойчивости. На рис.5.13 видно, что при увеличении К возрастает ωср и уменьшается запас устойчивости.

Рис.5.13. ЛЧХ при изменении К разомкнутой САУ
Повышение точности регулированием по интегралу от ошибки заключается в повышении порядка астатизма, что позволяет свести к нулю первые коэффициенты ошибок системы. Но в этом случае целесообразно повышать порядок астатизма без заметного или недопустимого снижения запаса устойчивости введением в САУ изодромных звеньев с передаточными функциями вида W(p)=(Tp+1)/τp, но не более 2-3. Постоянную времени изодромных звеньев Т надо брать большой, чтобы вносимый ими фазовый сдвиг не был существенным в области частоты среза ωср и не влиял на устойчивость системы. Регулирование по интегралу от ошибки ухудшает динамические свойства САУ, так как обычно Т изодромов обычно самые большие в системах.
При регулировании по производной от ошибки САУ начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. Введение производной увеличивает запасы устойчивости, что в конечном итоге позволяет повысить коэффициент разомкнутой системы (точность САУ), т.е. целесообразно использовать ПД - регуляторы с передаточными функциями вида W(p)= К(Tp+1), но не более 2-3 для обеспечения требуемой помехозащищенности.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного
П р и м е р. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рис.5.11.

Рис.5.11. Структурная схема САУ
Р е ш е н и е. Сначала необходимо привести исходную структурную схеме к одноконтурной, как показано на рис.5.12.

Рис.5.12. Приведенная структурная схема
Из рис. 5.12 видно, что при охвате идеального интегратора отрицательной обратной связью получается апериодическое звено 1-го порядка. Поэтому пользуясь правилом определения порядка астатизма, приведенным выше, можно заключить, и по управляющему, и по возмущающему воздействию астатизм равен 1.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
1. Дайте понятие качества работы системы управления. Чем оно определяется?
2. Что представляют собой критерии качества?
3. Как производится оценка точности работы систем?
4. Чему равны первые два коэффициента ошибок в системах с астатизмом первого и второго порядков?
5. Поясните связь частотных показателей качества работы системы с частотными характеристиками разомкнутой цепи.
6. Что представляют собой корневые оценки качества?
7. В чем удобство и недостатки интегральных критериев качества?
8. Каким образом экспериментальным путем можно оценить качество работы системы?
9. Какова роль моделирования систем управления?
10. Перечислите методы повышения точности работы САУ?
11. Что такое статическая и динамическая точность систем управления?
12. Как определить добротность по скорости и ускорению?
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обу
|










 = h(
= h( ) равно начальному значению вещественной частотной характеристики Р(0).
) равно начальному значению вещественной частотной характеристики Р(0). 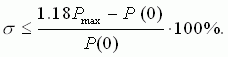
 .
. 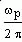 . Затухание этих колебаний тем меньше, чем острее и выше пик.
. Затухание этих колебаний тем меньше, чем острее и выше пик.  , то и переходный процесс h(t) может быть представлен суммой составляющих
, то и переходный процесс h(t) может быть представлен суммой составляющих  , где
, где 



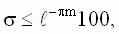
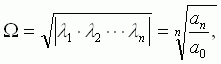
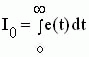
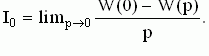
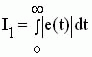
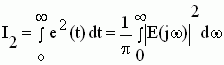

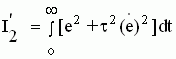
 =0 с желаемой постоянной времени τ, получившая название экстремаль.Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.
=0 с желаемой постоянной времени τ, получившая название экстремаль.Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.

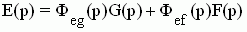
 - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
- передаточная функция замкнутой системы по ошибке относительно задающего воздействия. - передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.
- передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.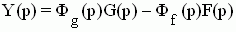 .
. - передаточная функция замкнутой системы по задающему воздействию.
- передаточная функция замкнутой системы по задающему воздействию.  - передаточная функция замкнутой системы по возмущающему воздействию.
- передаточная функция замкнутой системы по возмущающему воздействию. .
. .
.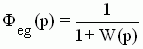
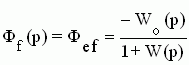
 ;
;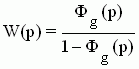 ; 4.
; 4.  .
.
 - установившееся значение ошибки от задающего воздействия;
- установившееся значение ошибки от задающего воздействия; - установившееся значение ошибки от возмущающего воздействия.
- установившееся значение ошибки от возмущающего воздействия. ,
,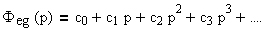
 при i=0, 1, 2, 3,...
при i=0, 1, 2, 3,...
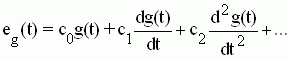
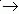 K при p
K при p 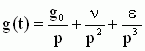 , где g0 - постоянная составляющая; ν - скоростная составляющая; ε - составляющая ускорения. Тогда установившееся значение ошибки управления будет
, где g0 - постоянная составляющая; ν - скоростная составляющая; ε - составляющая ускорения. Тогда установившееся значение ошибки управления будет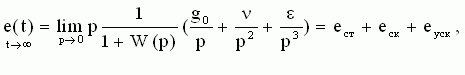
 = const - статическая ошибка; eск=
= const - статическая ошибка; eск= 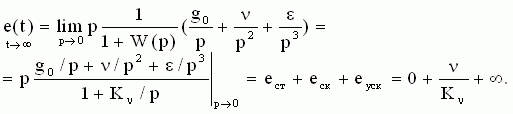
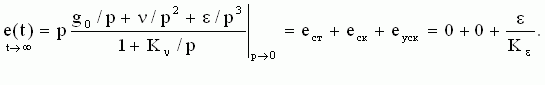

 , то установившаяся ошибка также будет изменяется по гармоническому закону с той же частотой:
, то установившаяся ошибка также будет изменяется по гармоническому закону с той же частотой: .
. .
. ,
,