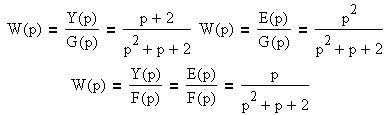Все типовые динамические звенья
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
| Типы объектов и законы регулирования
|  
|  
|  
| В зависимости от величины самовыравнивания различают три типа объектов управления: устойчивый (с положительным самовыравниванием); нейтральный (с нулевым самовыравниванием); неустойчивый (с отрицательным самовыравниванием). Признаком отрицательного самовыравнивания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения или появление отрицательного знака у свободного члена знаменателя передаточной функции (наличие положительного полюса).
Под законом регулирования (управления) понимается алгоритм или функциональная зависимость, определяющая управляющее воздействие u(t) на объект:
u(t) = F(Δ), где Δ - ошибка регулирования.
Законы регулирования бывают:
- линейные: 
или 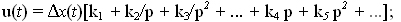 (3.1) (3.1)
- нелинейные:  . .
Кроме того, законы регулирования могут быть реализованы в непрерывном виде или в цифровом. Цифровые законы регулирования реализуются путем построения регуляторов с помощью средств вычислительной техники (микро ЭВМ или микропроцессорных систем).
Наличие в (3.1) чувствительности регулятора к пропорциональной, к интегральным или к дифференциальным составляющим в первичной информации x(t), определяет тип регулятора:
1. P - пропорциональный;
2. I - интегральный;
3. PI - пропорционально интегральный (изодромный);
4. PD - пропорционально дифференциальный;
5. и более сложные варианты - PID, PIID, PIDD,...
Нелинейные законы регулирования подразделяются на:
1. функциональные;
2. логические;
3. оптимизирующие;
4. параметрические.
В составе структуры САУ содержится управляющее устройство, которое называется регулятором и выполняет основные функции управления, путем выработки управляющего воздействия U в зависимости от ошибки (отклонения), т.е. U = f(Δ). Закон регулирования определяет вид этой зависимости без учёта инерционности элементов регулятора. Закон регулирования определяет основные качественные и количественные характеристики систем.
Рассмотрим основные линейные законы регулирования. Простейшим является пропорциональный закон и регулятор в этом случае называют Р-регулятором. При этом U=U0+kΔ, где U0-постоянная величина, k - коэффициент пропорциональности. Основным достоинством Р-регулятора является простота. По существу, это есть усилитель постоянного тока с коэффициентом усиления k. Недостатки Р - регулятора заключаются в невысокой точности регулирования.
Интегральный закон регулирования и соответствующий I - регулятор реализует следующую зависимость:
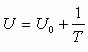 , где Т -постоянная времени интегрирования. , где Т -постоянная времени интегрирования.
Техническая реализация I - регулятора представляет собой усилитель постоянного тока с емкостной отрицательной обратной связью. I - регуляторы обеспечивают высокую точность в установившемся режиме за счет повышения порядка астатизма. Вместе с тем I - регулятор вызывает уменьшение устойчивости переходного процесса и системы в целом.
Пропорционально-интегральный закон регулирования позволяет объединить положительные свойства пропорционального и интегрального законов регулирования. В этом случае PI - регулятор реализует зависимость:
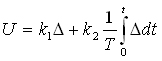
Мощным средством улучшения поведения САУ в переходном режиме является введение в закон регулирования производной от ошибки. Часто эта производная вводится в пропорциональный закон регулирования. В этом случае имеем пропорционально-дифференциальный закон регулирования, регулятор является РD- регулятором, который реализует зависимость:

Кроме PI и PD регуляторов, часто на практике используют PID -регуляторы, которые реализуют пропорционально-интегрально- дифференциальный закон регулирования:
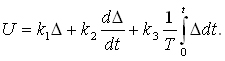
Структурная схема линейного стандартного регулятора приведена на рис.3.1.

Рис. 3.1. Структура линейного стандартного регулятора
Настройка такого регулятора заключается в задании значений коэффициентов пропорциональной, интегральной и дифференциальной составляющих таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного о
Важнейшей характеристикой САР и её составных элементов являются переходные и импульсные переходные (импульсные) функции.
Аналитическое определение переходных функций и характеристик основано на следующих положениях. Если задана передаточная функция системы или отдельного звена W(р) и известен входной сигнал X(t), то выходной сигнал Y(t) определяется следующим соотношением:

Таким образом, изображение выходного сигнала  представляет собой произведение передаточной функции на изображение входного сигнала представляет собой произведение передаточной функции на изображение входного сигнала  . Сигнал y(t) в явном виде получил после перехода от изображения . Сигнал y(t) в явном виде получил после перехода от изображения  к оригиналу y(t). Для большинства случаев линейных систем и составных элементов разработаны таблицы, позволяющие производить переход от изображений к оригиналу и обратно. В данном разделе представлена таблица 3.1 переходов для наиболее распространенных случаев. к оригиналу y(t). Для большинства случаев линейных систем и составных элементов разработаны таблицы, позволяющие производить переход от изображений к оригиналу и обратно. В данном разделе представлена таблица 3.1 переходов для наиболее распространенных случаев.
Так как изображение единичного ступенчатого воздействия равно 1/p, то изображение переходной функции определяется соотношением:

Следовательно, для нахождения переходной функции необходимо передаточную функцию разделить на p и выполнять переход от изображения к оригиналу.
Изображение единичного импульса равно 1. Тогда изображение импульсной функции определяется выражением:

Таким образом, передаточная функция является изображением импульсной функции.
Импульсная и переходная функции, как и передаточная функция, являются исчерпывающими характеристиками системы при нулевых начальных условиях. По ним можно определить выходной сигнал при произвольных входных воздействиях.
Таблица 3.1
Изображение по Лапласу и оригиналы
Изображение 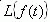
| Оригинал f(t)
| |
| 
| 
| 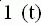
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 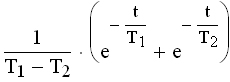
| 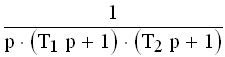
| 
| 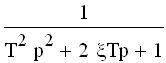
| 
| 
| 
| 
| 
| Передаточные функции и временные характеристики типовых звеньев приведены в таблице 3.2.
Таблица 3.2
Временные характеристики типовых звеньев
| Тип звена
| Передаточные функции
| Временные функции
| | Позиционные звенья
| | Усилительное
| 
| 
| | Апериодическое 1-го порядка
| 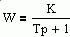
| 
| | Апериодическое 2-го порядка T1≥2T2
| 
| 
| | Колебательное 0<ξ<1
| 
| 
| | Консервативное
| 
| 
| | Интегрирующие звенья
| | Интегрирующее идеальное
| 
| 
| | Интегрирующее инерционное
| 
| 
| | Изодромное 1-го порядка
| 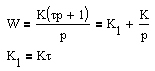
| 
| | Изодромное 2-го порядка
| 
| 
| | Дифференцирующие звенья
| | Идеальное дифференцирующее
| 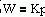
| 
| | Дифференцирующее инерционное
| 
| 
| | Форсирующее 1-го порядка
| 
| 
| © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
В условиях реальной эксплуатации САУ часто возникает необходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САУ, если на один из входов подается периодически сигнал гармонической формы. Решение этой задачи возможно получить путем использования частотных характеристик. Частотные характеристики могут быть получены экспериментальным или аналитическим путем. При аналитическом определении исходным моментом является одна из передаточных функций САУ (по управлению или по возмущению). Возможно также определение частотных характеристик исходя из передаточных функций разомкнутой системы и передаточной функции по ошибке.
Если задана передаточная Функция W(р), то путём подставки p=jω получаем частотную передаточную функцию W(jω), которая является комплексным выражением т.е. W(jω)=U(ω)+jV(ω), где U(ω) - вещественная составляющая, а V(ω) - мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме:
W(jω)=A(ω)ejφ(ω) (3.2)
, где  - модуль; - модуль;  - аргумент частотной передаточной функции. - аргумент частотной передаточной функции.
Функция A(ω), представленная при изменении частоты от 0 до  получило название амплитудной частотной характеристики (АЧХ). получило название амплитудной частотной характеристики (АЧХ).
Функция Φ(ω), представленная при изменении частоты от 0 до  называется фазовой частотной характеристикой (ФЧХ). называется фазовой частотной характеристикой (ФЧХ).
Таким образом, дифференциальное уравнение движения системы связывает входной и выходной сигналы (т.е. функции времени), ПФ связывает изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры.
Частотная передаточная функция W(jω) может быть представлена на комплексной плоскости. Графическое отображение для всех частот спектра отношений выходного сигнала САУ к входному, представленных в комплексной форме будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ) или годограф Найквиста. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного - АЧХ, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка - ФЧХ. При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, а положительный фазовый сдвиг представляется вращением против часовой стрелки.
Для упрощения графического представления частотных характеристик, а также для облегчения анализа процессов в частотных областях используются логарифмические частотные характеристики: логарифмическая амплитудная частотная характеристика (л.а.ч.х.) и логарифмическая фазовая частотная характеристика (л.ф.ч.х.). При построении логарифмических характеристик на шкале частот вместо ω откладывается lg(ω) и единицей измерения является декада. Декадой называется интервал частот, соответствующий изменению частоты в 10 раз. При построений л.а.ч.х. на оси ординат единицей измерения является децибел [дБ], который представляет собой соотношение L=20 lg А(ω). Один децибел представляет собой увеличение амплитуды выхода в  раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды). Точка пересечения л.а.х. с осью абсцисс соответствует частоте среза ωср, при которой амплитуда выходного сигнала равна входной. раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды). Точка пересечения л.а.х. с осью абсцисс соответствует частоте среза ωср, при которой амплитуда выходного сигнала равна входной.
Для л.ф.ч.х. на оси частот используется логарифмический масштаб, а для углов - натуральный масштаб. На практике логарифмические частотные характеристики строятся на совмещённой системе координат, которые представлены на рис. 3.2.

Рис 3.2. Схема координат для логарифмических характеристик
Главным достоинством логарифмических частотных характеристик является возможность построения их во многих случаях практически без вычислительной работы, т.е. строить асимптотические л.ч.х.. Особенно удобно использовать логарифмические частотные характеристики при анализе всей системы, когда результирующая передаточная функция после разложения на множители приводится к виду:
 (3.3) (3.3)
т.е. передаточную функцию любой САУ в общем случае можно представить как произведение передаточных функций следующего вида:
 - где: Kr, r, T, ξ, - постоянные величины, причём Kr>0, r>0, T>0, 0<ξ<1. - где: Kr, r, T, ξ, - постоянные величины, причём Kr>0, r>0, T>0, 0<ξ<1.
В этом случае построение л.а.х. производится по выражению

Построение л.ф.х. производится по выражению 
Таким образом, результирующая л.а.х. определяется суммированием л.а.х. составляющих типовых звеньев, а результирующая л.ф.х. - соответственно суммированием л.ф.х. составляющих типовых звеньев.
Пример задачи
Частотные характеристики типовых звеньев приведены в таблице 3.3
Таблица 3.3
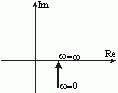
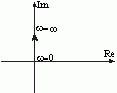
Частотные характеристики звеньев
| Частотная передаточная функция
| Амплитудная и фазовая характеристики
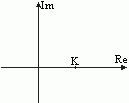
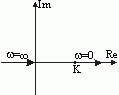
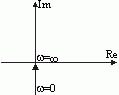
| Амплитудно-фазовая частотная характеристика
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 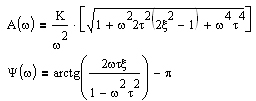
| 
| 
| 
| 
| 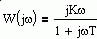
| 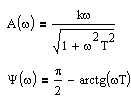
| 
| 
| 
| 
| 
| 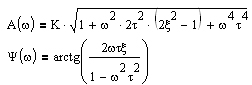
| 
| © В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
| Методы определения характеристик
|  
|  
|  
| В том случае, когда работа отдельного устройства или системы в целом не может быть точно описана дифференциальными уравнениями, возможно экспериментальное определение динамических характеристик.
Экспериментальные методы определения динамических характеристик звеньев и систем делятся на два класса: методы определение временных характеристик объекта управления и методы определение частотных характеристик объекта управления. Временные методы определения динамических характеристик делятся, в свою очередь, на активные и пассивные.
Активные методы предполагает подачу на вход объекта пробных тестирующих сигналов - детерминированных или случайных. В зависимости от вида пробного сигнала выбирают соответствующие методы обработки выходного сигнала системы. Так, например, при подаче ступенчатого управляющего сигнала, снимают кривую разгона (переходную характеристику), а при подаче - функции снимают кривую отклика (функцию веса). Кривая отклика снимается для устройств, не допускающих подачу на вход ступенчатых сигналов. Достоинствами активных методов являются: достаточно высокая точность получения математического описания; относительно малая длительность эксперимента. Следует учитывать, что активные методы, в той или иной степени, приводят к нарушению нормального хода технологического процесса. Поэтому проведение эксперимента должно быть тщательно спланировано. В пассивных методах на вход объекта не подаются никакие пробные сигналы, а лишь фиксируется естественное движение объекта в процессе его нормального функционирования. Полученные реализации массивов данных входных и выходных сигналов обрабатываются статистическими методами. По результатам обработки получают параметры передаточной функции объекта. Такие методы имеют ряд недостатков: малая точность получаемого математического описания; необходимость накопления больших массивов данных с целью повышения точности; если эксперимент проводится с устройством, охваченным обратной связью, то наблюдается эффект корреляции (взаимосвязи) между входом и выходом устройства через регулятор. Такая взаимосвязь снижает точность математического описания.
Частотные методы определения динамических характеристик предполагают, что на вход минимально-фазового устройства подается гармонический сигнал с известной частотой и амплитудой. Модуль амплитудно-фазовой характеристики определяется как отношения амплитуды выходной гармоники к амплитуде входной. Фазовая характеристика характеризует фазовый сдвиг между этими гармониками на различных частотах пробного сигнала. Эти характеристики могут определяться непосредственно по графикам входного и выходного сигналов устройств, либо методом синхронного детектирования. Частотные методы определения динамических характеристик поводятся в два этапа: на первом этапе определяется а.ф.х. или а.ф.х., а на втором - передаточная функция. Амплитудно-фазовая характеристика (АФХ) объекта несет большую информацию об объекте, чем его кривая разгона. Таким образом, определение динамики объекта управления по его АФХ позволяет получить более точную динамическую модель, работающую в широком диапазоне частот. Однако при определении динамических характеристик объекта с помощью частотных методов следует учитывать, что они более трудоемки и требуют наличия специальной аппаратуры (низкочастотные генераторы периодических сигналов, регистрирующая аппаратура - двухлучевой осциллограф). Изменяя частоту входного сигнала в требуемом диапазоне снимают осциллограммы и по ним определяют 20lg(Авых/Авх) и Φi(ωi). Полученные значения наносятся на полулогарифмическую бумагу соответствующими точками и через них проводятся прямые с типовыми наклонами. В точках пересечения этих прямых находятся соответствующие параметры исследуемого устройства или системы.
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения
В табл. 3.2 и 3.3 указаны лишь характеристики основных типовых звеньев. Кроме того существуют интегро-дифференцирующие звенья и неминимально-фазовые звенья. Интегро-дифференцирующие звенья имеют передаточные функции вида:

где: k-постоянный коэффициент; R(p) и Q(p)- полиномы от p первого или второго порядков.
К неминимально-фазовым звеньям относятся неустойчивые звенья, передаточные функции которые имеют хотя 6ы один положительный полюс (отрицательное самовыравнивание) или положительный нуль. Одной амплитудной частотной характеристике неминимально-фазовых звеньев может соответствовать несколько различных фазовых частотных характеристик.
Например, звено с положительным полюсом имеет передаточную функцию вида (пример неустойчивого объекта):

При положительном полюсе (корень знаменателя) p = 1/T частотные характеристики имеют вид:

Неминимально-фазовыми являются также звенья, которые имеют бесконечное число полюсов в левой части комплексной плоскости. Эти звенья известны под названием звенья чистого запаздывания, у которых выходная величина повторяет входную с некоторой задержкой во времени. Уравнение и передаточная функция звена (с учетом разложения в ряд Тейлора):

где τ - время чистого запаздывания. Частотные характеристики:
 [рад.] [рад.]
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
| Правила структурных преобразований
|  
|  
|  
| Обычно структурная схема САУ состоит из отдельных элементов, соединенных последовательно, параллельно или с помощью обратных связей, т.е. САУ можно рассматривать как комбинацию типовых динамических звеньев. Изображение системы управления в виде совокупности типовых и нетиповых динамических звеньев с указанием связей между ними носит название структурной схемы системы. Звено в этом случае выступает как элементарная структурная единица, преобразователь информации. Каждый элемент имеет один вход и один выход и заданную передаточную функцию.
Существуют следующие правила структурных преобразований, позволяющие по передаточным функциям отдельных элементов определить требуемую передаточную функцию.
При последовательном соединении элементов передаточные функции перемножаются. При параллельном соединении передаточные функции суммируются. Правила структурных преобразований при наличии обратных связей (встречно-параллельное соединение) представлены на рис 3.3.

Рис. 3.3. Правила структурных преобразований при наличии обратных связей: а - положительная, б - отрицательная.
Если задана многоконтурная структура САУ, то с помощью структурных преобразований она может быть приведена к одноконтурной. При этом используется ряд дополнительных правил, связанных с переносом элементов структурной схемы. Эти правила сведены в таблицу 3.4.
Таблица 3.4
Правила структурных преобразований
| Преобразование
| Структурная схема
| | Исходная
| Эквивалентная
| | Перенос узла через элемент
| 
|  
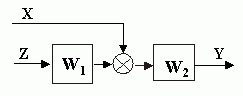
| | Перенос сумматора через элемент
| 
|  
| | Перемена мест узла и сумматора
| 
| 
| | Перенос сумматора через сумматор
| 
| 
| | Перенос узла через узел
| 
| 
| Более полный перечень правил структурных преобразований представлен в учебном пособии [2,6].
Пример задачи
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
П р и м е р: построить л.а.х. и л.ф.х. системы, описываемой передаточной функцией W(p)=100/(0.1p+1)(0.01p+1).
Р е ш е н и е. Представим передаточную функцию в виде произведения элементарных звеньев 
Низкочастотный участок л.а.х. пойдет с наклоном 0 дБ/дек на уровне 20 lg 100= 40 дБ. Частоты сопряжения для апериодических составляющих будут соответственно ω1=1/0.1=10 и ω2=1/0.01=100. Фазочастотная характеристика строится в соответствии с уравнением Φ(ω)= arctg (0.1ω) + arctg (0.01ω). Ниже представлены графики л.а.х. и л.ф.х., соответствующие заданной передаточной функции.

П р и м е р: определить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже

Р е ш е н и е. Двигаясь по л.а.х. в направлении возрастания частоты определяем, что звено принадлежит к дифференцирующему типу, т.к. наклон низкочастотного участка равен +20дБ/дек (+1). Передаточная функция равна W(p)=0.2p. При частоте излома л.а.х. ω=50 наклон меняется на -20дБ/дек (-1). Очевидно добавлены два звена с передаточной функцией 
Тогда суммарная передаточная функция, соответствующая заданной л.а.х. будет иметь вид 
П р и м е р: пользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:

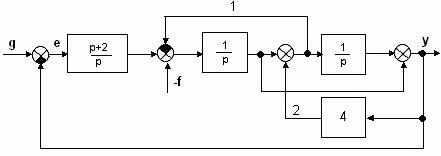
Рис.3.4. Структурная схема многоконтурной САУ
Р е ш е н и е: перед тем, как находить передаточные функции необходимо освободиться от перекрестных связей 1 и 2 на рис.3.4, для чего необходимо перенести или узел, или сумматор с добавлением соответствующих звеньев. Кроме того, целесообразно привести возмущающее воздействие f(t) ко входу САУ. Тогда получим схему на рис.3.5.

Рис.3.5. Преобразованная структурная схема без перекрестных связей
Пользуясь правилами структурных преобразований свернем внутренние контура и получим одноконтурную замкнутую САУ на рис.3.6.

Рис.3.6. Одноконтурная структурная схема САУ
Тогда требуемые передаточные функции замкнутой САУ запишем в виде:
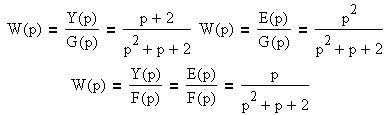
Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики, а так же получить качественные и количественные оценки динамики и статики САУ.
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучения.
1. Что такое динамическое звено и его характеристика?
2. Дайте определение основных характеристик.
3. Какие частотные характеристики используются для исследования систем?
4. Почему ЛЧХ нашли большое применение в инженерной практике?
5. По каким признакам классифицируются типовые динамические звенья?
6. Перечислите группы основных типов звеньев.
7. Что представляет собой структурная схема системы управления?
Какие способы соединений звеньев используются в системах?
8. Как находятся передаточные функции смешанных соединений звеньев?
9. Каким образом строятся логарифмические частотные характеристики разомкнутой цепи звеньев?
10. Постройте ЛЧХ типовых звеньев.
11. В чем заключается принцип суперпозиции?
12. В чем особенность направленного действия типовых звеньев?
© В.Н. Бакаев, Вологда 2004. Разработка электронной версии: М.А.Гладышев, И.А. Чуранов.
Вологодский Государственный Технический Университет.
Кафедра Дистанционного и Заочного обучени
|










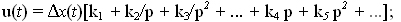 (3.1)
(3.1)  .
.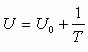 , где Т -постоянная времени интегрирования.
, где Т -постоянная времени интегрирования.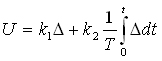

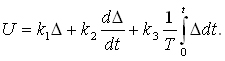


 представляет собой произведение передаточной функции на изображение входного сигнала
представляет собой произведение передаточной функции на изображение входного сигнала  . Сигнал y(t) в явном виде получил после перехода от изображения
. Сигнал y(t) в явном виде получил после перехода от изображения 

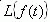


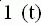











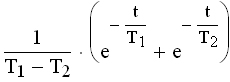
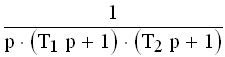

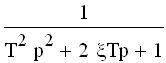







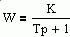











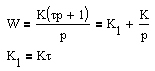



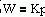





 - модуль;
- модуль;  - аргумент частотной передаточной функции.
- аргумент частотной передаточной функции. получило название амплитудной частотной характеристики (АЧХ).
получило название амплитудной частотной характеристики (АЧХ). раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды). Точка пересечения л.а.х. с осью абсцисс соответствует частоте среза ωср, при которой амплитуда выходного сигнала равна входной.
раз. Верхняя полуплоскость л.а.х. соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды). Точка пересечения л.а.х. с осью абсцисс соответствует частоте среза ωср, при которой амплитуда выходного сигнала равна входной. 
 (3.3)
(3.3)  - где: Kr, r, T, ξ, - постоянные величины, причём Kr>0, r>0, T>0, 0<ξ<1.
- где: Kr, r, T, ξ, - постоянные величины, причём Kr>0, r>0, T>0, 0<ξ<1. 


























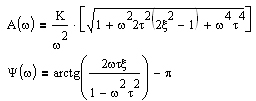




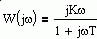
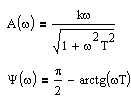





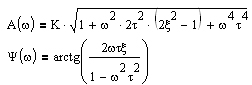





 [рад.]
[рад.]