
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы анализа эффективности работы транспортСодержание книги
Поиск на нашем сайте
В работе имеются динамические ряды, характеризующие эффективность работы транспорта за ряд лет. При проведении анализа этих динамических рядов будут использованы следующие показатели динамики. Абсолютный приростхарактеризует размер увеличения (или уменьшения) уровня ряда за определенный промежуток времени. Он равен разности двух сравниваемых уровней и выражает абсолютную скорость роста:
где
Обобщающим показателем абсолютной скорости изменения явления во времени является средний абсолютный приростза весь период:
Темп роста характеризует отношение двух сравниваемых уровней ряда в виде:
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста:
Темп прироста характеризует абсолютный прирост в относительных величинах:
Средний темп прироста:
Абсолютное значение одного процента прироста представляет собой одну сотую часть базисного уровня и в то же время – отношение абсолютного прироста к соответствующему темпу прироста:
При анализе структуры и ее изменений будут использованы относительные показатели структуры в долях или удельных весах, представляющих собой соотношения размеров частей и целого. Также будут использованы частные и обобщающие показатели структурных сдвигов. «Абсолютный» прирост удельного веса
где
Темп роста удельного весапредставляет собой отношение удельного веса
Линейный коэффициент «абсолютных» структурных сдвигов:
где
Этот показатель отражает то среднее изменение удельного веса (в процентных пунктах), которое имело место за рассматриваемый временной интервал в целом по всем структурным частям совокупности. Среднеквадратический коэффициент «абсолютных» структурных сдвигов:
Для сводной характеристики интенсивности изменения удельных весов используется среднеквадратический коэффициент относительных структурных сдвигов:
Данный показатель отражает тот средний относительный прирост удельного веса в процентах, который наблюдался за рассматриваемый период [19]. Интегральный коэффициент Гатева:
где
Индекс Салаи:
Индекс Рябцева:
Интегральный коэффициент Гатева, индекс Салаи и индекс Рябцева изменяются в пределах [0;1]; чем ближе к единице, тем сильнее изменение структуры [20]. Для наглядного представления результатов анализа динамики и структуры будет применен графический метод. При исследовании эффективности работы транспорта применяются линейные и столбиковые диаграммы [18]. Графическое изображение во многих случаях позволяет приближенно выявить тип тенденции временного ряда, но прежде чем переходить к определению тенденции и выделению тренда, нужно выявить, существует ли тенденция в исследуемом процессе. Для этой цели разработано множество критериев. В работе для проверки гипотезы об отсутствии тенденции во временном ряду применяется критерий серий, основанные на медиане выборки. Он включает следующие шаги: 1) Выдвигается гипотеза об отсутствии тренда. 2) Из исходного ряда показателя эффективности работы транспорта образуется ранжированный ряд. 3) Определяется медиана ранжированного ряда ( 4) Образуется последовательность
Если значение уровня исходного ряда совпадает с медианой, то значение пропускается. 5) Подсчитывается 6) Для того, чтобы гипотеза о случайности исходного ряда не была отвергнута должны выполняться следующие неравенства:
где
Если хотя бы одно из неравенств нарушается, то гипотеза отклоняется с вероятностью ошибки Так как в данной дипломной работе будут использованы временные ряды за ряд лет в помесячном разрезе, то будут построены тренд - сезонные модели и модель регрессии с включением фактора времени и фиктивными переменными. Алгоритм построения тренд-сезонной аддитивной модели: 1. Проводятся сглаживание временного ряда с помощью простой скользящей средней. 2. Рассчитываются абсолютные показатели сезонности:
где
3. Рассчитаются средние показатели сезонности для одноименных месяцев:
4. Если сумма средних показателей сезонности не равна нулю,проводится их корректировку по формуле:
5. Проводятся десезоналирование временного ряда:
6. По десезоналированному временному ряду проводят аналитическое выравнивание. 7. Рассчитается тренд с учетом сезонности:
Алгоритм построения тренд - сезонной мультипликативной модели: 1. Сглаживание временного ряда с помощью скользящей средней. 2. Рассчитывается коэффициент сезонности:
3. Определяются средние показатели сезонности для одноименных месяцев:
4. Если сумма средних коэффициентов сезонности не равна 12,проводится их корректировку по формуле:
5. Исключается сезонность из уровней ряда:
6. Проводятся аналитическое выравнивание десезоналированного ряда. 7. Рассчитывается уровни временного ряда, обусловленные влиянием тенденции и сезонности:
В данной дипломной работы будут также построены модели стационарных рядов. Алгоритм построения данных моделей включает следующие шаги: 1. Проверка ряда на стационарность. 2. Преобразование ряда при условии его нестационарности. 3. Идентификация базового набора моделей. 4. Оценивание параметров моделей. 5. Проверка на адекватность и окончательный выбор модели. 6. Использование модели для прогнозирования [24]. Так как в данной дипломной работе для моделирования показателей эффективности работы транспорта будут построены различные модели, то необходимо провести проверку адекватности построенных моделей реальному процессу, а также оценить точность данных моделей. Проверка адекватности строится на анализе случайной остаточной компоненты
Модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения. Существует несколько приемов обнаружения автокорреляции: Критерий Дарбина – Уотсона, метод рядов, Q-тест Льюинга – Бокса. В данной дипломной работе будет использован метод рядов. Алгоритм метода рядов заключается в следующем: 1. Последовательно определяется знаки отклонений. 2. Подсчитывается количество рядов (k) и длина ряда. Если рядов слишком мало по сравнению с количеством наблюдений (n), то вполне вероятно наличие положительной автокорреляции. Если же рядов слишком много, вероятно наличие в остатках отрицательной автокорреляции. 3. Пусть Если при достаточно большом количестве наблюдений, количество рядов k лежит в пределах:
то гипотеза об отсутствии автокорреляции не отклоняется. Если значения остаточной компоненты удовлетворяют вышеперечисленным свойствам, то данное уравнение тренда можно использовать для прогнозирования показателей эффективности работы транспорта [21]. Важнейшими характеристиками качества, выбранной для прогнозирования модели, являются показатели ее точности: 1) средняя относительная ошибка по модулю:
Если 2) дисперсия или среднеквадратическая ошибка прогноза:
Чем меньше значение этих характеристик, тем выше точность моделей [25]. В данной дипломной работе будет произведено многофакторное моделирование показателей эффективности работы транспорта, перед тем как перейти непосредственно к моделированию необходимо проверить гипотезу об отсутствии в коинтеграции временных рядов. Одним из методов тестирования гипотезы является критерий Энгеля– Грэнджера. Алгоритм Энгеля– Грэнджера: 1. Выдвигается нулевая гипотеза об отсутствии коигтеграции между рядами. 2. Рассчитываются параметры уравнения регрессии вида:
3. Определяют фактическое значение t-критерия Стьюдента для коэффициента регрессии. 4. Сравнивают полученное значение с критическим значением Другой метод тестирования гипотезы коинтеграции между временными рядами основан на использовании величины критерия Дарбина-Уотсона. Если фактическое значение критерия Дарбина-Уотсона меньше критического для заданного уровня значимости, то нулевая гипотеза об отсутствии коинтеграции не отклоняется. Коинтеграция временных рядов значительно упрощает процедуры и методы, используемые в целях их анализа, поскольку в этом случаи можно строить уравнение регрессии и определять показатели корреляции, применяя в качестве исходных данных непосредственно уровни изучаемых рядов, учитывая тем самым информацию, содержащуюся в исходных данных, в полном объеме [22]. При подстановке значений в уравнение модели получаем точечный прогноз. Так как нельзя исключать ошибку прогноза, которая всегда присутствует, необходимо построить интервальный прогноз. Доверительные интервалы прогноза определяется по формуле:
Таким образом, значение показателя эффективности работы транспорта на некий прогнозный период с вероятностью
Прогнозирование экономических показателей с применением различных методов приводит к необходимости сравнений полученных моделей. При этом часто получают модели со сходными статистическими свойствами, в результате чего трудно сделать предпочтение какой-либо модели. Поэтому необходимо осуществить объединение частных прогнозов, которое можно с помощью построения средневзвешенного прогноза и на основе факторного анализа. На основе двух частных прогнозов строится средневзвешенный прогноз, для этого находят веса для частных прогнозов, используя следующую формулу:
При определении весов учитываются Алгоритм построения обобщенного прогноза на основе факторного анализа. Для того чтобы получить обобщенный прогноз через частные прогнозы, выраженные в их естественных единицах измерения, следует привести стандартизацию показателей
Тогда
где
Однако оценки, полученные таким образом, могут оказаться как положительными, так и отрицательными. Обобщенный прогноз примет вид:
где
Таким образом, обобщенный прогноз получается путем ортогонального преобразования центрированных переменных
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.211.55 (0.01 с.) |

 , (1.3)
, (1.3) – уровень текущего периода,
– уровень текущего периода, – уровень предыдущего периода.
– уровень предыдущего периода. . (1.4)
. (1.4) . (1.5)
. (1.5) . (1.6)
. (1.6)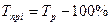 . (1.7)
. (1.7)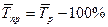 . (1.8)
. (1.8) [17, 18]. (1.9)
[17, 18]. (1.9) -ой части совокупности показывает, на сколько процентных пунктов возросла или уменьшилась данная структурная часть в
-ой части совокупности показывает, на сколько процентных пунктов возросла или уменьшилась данная структурная часть в  -ый период по сравнению с (
-ый период по сравнению с ( ) периодом:
) периодом: , (1.10)
, (1.10) – удельный вес
– удельный вес  – удельный вес
– удельный вес 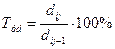 (1.11)
(1.11) , (1.12)
, (1.12) – число структурных частей.
– число структурных частей. . (1.13)
. (1.13) . (1.14)
. (1.14) , (1.15)
, (1.15) и
и  – удельные веса градаций двух структур.
– удельные веса градаций двух структур. . (1.16)
. (1.16) . (1.17)
. (1.17) ).
). из «плюсов» и «минусов» по следующему правилу:
из «плюсов» и «минусов» по следующему правилу: (1.18)
(1.18)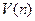 – число серий в совокупности
– число серий в совокупности 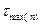 – протяженность самой длинной серии.
– протяженность самой длинной серии. , (1.19)
, (1.19) , (1.20)
, (1.20) – число наблюдений.
– число наблюдений. , то есть подтверждается наличие тренда [25].
, то есть подтверждается наличие тренда [25]. , (1.21)
, (1.21)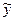 – выровненные скользящие средние.
– выровненные скользящие средние. . (1.22)
. (1.22) . (1.23)
. (1.23) . (1.24)
. (1.24) . (1.25)
. (1.25) =
=  . (1.26)
. (1.26) . (1.27)
. (1.27) . (1.28)
. (1.28) . (1.29)
. (1.29) [21]. (1.30)
[21]. (1.30) :
: . (1.31)
. (1.31) – общее количество знаков «+»;
– общее количество знаков «+»;  – общее количество знаков «–».
– общее количество знаков «–». , (1.32)
, (1.32) % (1.33)
% (1.33) , это свидетельствует о высокой точности модели, при
, это свидетельствует о высокой точности модели, при  – точность хорошая, при
– точность хорошая, при 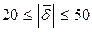 % – удовлетворительная.
% – удовлетворительная. (1.34)
(1.34) . (1.35)
. (1.35) . (1.36)
. (1.36) . Если критическое значение t-критерия Стьюдента больше
. Если критическое значение t-критерия Стьюдента больше  . (1.37)
. (1.37)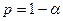 будет заключено в интервале:
будет заключено в интервале: [6]. (1.38)
[6]. (1.38) . (1.39)
. (1.39) последних ошибок частных прогнозов. На практике стремятся придать больший вес тому набору прогнозов, который содержит меньшие по величине среднеквадратические ошибки.
последних ошибок частных прогнозов. На практике стремятся придать больший вес тому набору прогнозов, который содержит меньшие по величине среднеквадратические ошибки. :
: . (1.40)
. (1.40) , (1.41)
, (1.41)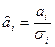 .
. , (1.42)
, (1.42) ;
; .
. . При этом угол поворота выбирается таким образом, чтобы минимизировать норму внедиагональной части остаточной корреляционной матрицы частных прогнозов [23].
. При этом угол поворота выбирается таким образом, чтобы минимизировать норму внедиагональной части остаточной корреляционной матрицы частных прогнозов [23].


