Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 12. Язык логики предикатов.Содержание книги
Поиск на нашем сайте
Определение. Предикатом Иначе говоря, Для любых Всякой функции В дальнейшем, в случаях, не вызывающих разночтения, будем употреблять одинаковые обозначения для предикатов и соответствующих им отношений. При этом, помимо функциональных обозначений вида Пример 1. а) Предикат б) Великая теорема Ферма (до сих пор не доказанная) утверждает, что для любого натурального числа в) В описаниях вычислительных процедур и, в частности, в языках программирования, часто встречаются указания типа “повторять цикл до тех пор, пока переменные
Пусть Высказывание “существует такое значение Смысл связанных и свободных переменных в предикатах принципиально различен. Свободная переменная – это обычная переменная, которая может принимать различные значения из множества Навешивать кванторы можно и на многоместные предикаты и вообще на любые логические выражения, которые при этом заключаются в скобки. Выражение, на которое навешивается квантор Пример 2. а) Пусть б) Рассмотрим двухместный предикат
При логической (истинностной) интерпретации формул логики возможны три основные ситуации. 1. Если в области 2. Если формула 3. Если формула Определение. Формулы называются эквивалентными, если при любых подстановках одинаковых констант они принимают одинаковые значения. В частности, все тождественно истинные (и все тождественно ложные) формулы являются эквивалентными. Отметим, что если формулы Замечание. Исследование формул логики предикатов имеет огромное значение потому, что эти формулы входят практически в любую формальную теорию. В связи с этим возникают две проблемы: получение истинных формул и проверка имеющихся формул на истинность. Поскольку предикатные переменные имеют, в общем случае, бесконечное множество значений, то установить истинность формул простым перебором значений на всех наборах переменных, как это иногда делалось для логических функций, просто невозможно. В связи с этим, приходится использовать различные косвенные приёмы. Пример 3. Рассмотрим соотношение Аналогично доказывается истинность соотношения Большое значение имеют следующие свойства, которые могут быть доказаны способом, рассмотренным в примере 3. 1) Дистрибутивность квантора
2) Дистрибутивность квантора
Если же кванторы 3) 4) В таких случаях говорят, что левая часть является более сильным утверждением, чем правая, поскольку она требует для своего выполнения более жёстких условий. Так, например, в соотношении 3 в левой части требуется, чтобы оба предиката были истинны для одного и того же значения Пусть 5) 6) 7) 8) Эти соотношения означают, что формулу, не содержащую переменной
Метод доказательства формул, содержащих переменные, путём непосредственной подстановки в них констант называется методом интерпретаций или методом моделей. Подстановка констант позволяет интерпретировать формулу как осмысленное утверждение об элементах конкретного множества. Поэтому такой метод, выясняющий истинность формулы путём обращения к её возможному смыслу называется семантическим (смысловым). Метод интерпретаций удобен для доказательства выполнимости формул или их неэквивалентности, поскольку и в том, и в другом случае достаточно найти одну подходящую подстановку. Он удобен также для исследования истинности формул на конечных областях. Дело в том, что если область
Заменяя все кванторы по этим соотношениям, любую формулу логики предикатов можно перевести в формулу, состоящую из предикатов, соединённых логическими операциями. Истинность такой формулы на конечной области проверятся конечным числом подстановок и вычислений. Методы рассуждений, использующие только конечные множества конечных объектов, называются финитными. Для бесконечных же областей, в общем случае, при доказательстве тождественной истинности формул метод интерпретации связан с большими трудностями. Поэтому для построения множества истинных формул в логике предикатов выбирается иной путь. Это множество порождается из неких исходных формул (аксиом) с помощью формальных процедур - правил вывода. Используются лишь формальные (а не содержательные), внешние свойства последовательности символов, образующих формулы, причём эти свойства полностью описываются правилами вывода. Множества, порождённые таким формальным методом, называются формальными.
Назад, в начало конспекта.
Лекция № 13. Комбинаторика. В этой лекции даются основные начальные сведения из комбинаторики. Это служебный раздел математики, занимающийся исследованием различных комбинаций элементов всевозможных множеств. Формулы комбинаторики широко используются теории вероятностей, в теории вычислительных машин, в некоторых разделах экономике, в статистике и других прикладных дисциплинах.
Будем в дальнейшем оперировать только с множествами, содержащими конечное число элементов. На бесконечные множества все нижеприведённые правила и формулы не распространяются. Теорема 13.1. Пусть даны непересекающиеся конечные множества
Доказательство этой теоремы очевидно. Но для нас представляет интерес другая интерпретация этой теоремы, которую мы сформулируем для двух множеств. Если некоторый элемент Пусть даны непересекающиеся конечные множества Теорема 13.2. Число элементов в декартовом произведении множеств
Как и в предыдущем случае, сформулируем данную теорему упрощённым образом для двух множеств. Если элемент Оба сформулированных правила верны для любого конечного числа конечных множеств, и, в соответствующей форме, называются обобщёнными. Пример 1. а) В некоторой средней школе имеется три пятых класса, в которых обучаются соответственно 28, 31 и 26 учащихся. Требуется одного из них выбрать для участия в совете школы. Сколькими способами можно сделать выбор? По правилу суммы получаем б) В секции фигурного катания занимаются 14 мальчиков и 18 девочек. Сколькими различными способами из детей, занимающихся в секции, можно образовать спортивные пары. По правилу произведения получаем
Определение. Любой вектор длины Пример 2. Куплено различных 12 книг. На полке можно поставить в ряд ровно 6 книг. Сколькими различными способами можно это сделать? Будем считать различными не только те случаи, когда берутся разные книги, но и когда они по-разному расставлены на полке (в различном порядке). Тогда речь идёт о перестановках по 6 из 12. Получаем: Рассмотрим существенно другой случай, а именно когда элементы множества Определение. Любой вектор длины Пример 3. Сколько различных комбинаций может получиться при одновременном бросании трёх игральных костей? Каждая игральная кость представляет собой кубик, на гранях которого нанесено от одного до 6 очков. При каждом бросании мы будем получать наборы вида Замечание. Очевидно, что размещения без повторений являются частным случаем размещений с повторениями.
Определение. Любой вектор длины Из определения и формулы видно, что перестановки без повторений есть частный случай размещений без повторений, при условии Пример 4. Сколькими различными способами можно расставить на полке 10 различных книг? Здесь, в отличие от примера 2, значение имеет только порядок расставляемых книг. Поэтому речь идёт о перестановках из 10 элементов. Получаем: Рассмотрим случай, когда элементы множества Положив в последней формуле Пример 5. Сколько различных шестизначных чисел могут быть записано с помощью цифр 1, 2, 2, 2, 3, 3? Имеется набор из шести цифр, в котором цифра 2 повторяется трижды и цифра 3 – дважды. Полученные числа будут представлять собой перестановки с повторениями из 6 элементов. Получаем:
Прежде всего, отметим одно существенное отличие перестановок от размещений. Если в размещениях векторы различаются и по составу элементов, и по их расположению (порядку) в наборе, то в перестановках векторы различаются только по расположению элементов. Естественно рассмотреть случай, когда векторы, наоборот, будут различаться только по составу элементов. Определение. Любые различные векторы длины Если все элементы, образующие сочетания, различны, то их называют сочетанием без повторений. Обозначение всех сочетаний без повторений Замечание 1. Сочетания являются частным случаем размещений. Разница между сочетаниями и размещениями из определения неочевидна, но на конкретных примерах её легко видеть. Так, например, векторы Замечание 2. Для сочетаний без повторений обязательно требование Пример 6. а) В отделе работают 10 сотрудников. Требуется отобрать трёх из них для того, чтобы направить в командировку. Сколькими способами можно это сделать? Поскольку имеет значение только то, какие именно сотрудники отобраны, то речь идёт о сочетаниях без повторений по 3 элемента из 10. Получаем: б) В цветочном магазине имеются в продаже 5 различных видов цветов. Покупателю требуется составить букет из 7 цветов. Сколькими способами можно это сделать? Будем считать различными те букеты, которые отличаются друг от друга по подбору цветов. Поскольку цветы в букете могут повторяться, то речь идёт о сочетаниях с повторениями по 7 элементов из 5. Тогда получим Одним из наиболее известных примеров использования комбинаторных формул является так называемый бином Ньютона. В общем виде формула бинома (двучлена) Ньютона выглядит так:
С частными случаями применения этой формулы (для случаев
На практике для удобства применении бинома Ньютона применяют так называемый треугольник Паскаля, который содержит числовые коэффициенты полинома в правой части формулы: 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 …………………..
Назад, в начало конспекта.
РАЗДЕЛ IV. ТЕОРИЯ ГРАФОВ.
Лекция № 14. Графы: основные понятия и операции. Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В дальнейшем оказалось, что понятие графа можно применять не только при исследовании геометрических конфигураций. Особенно часто определяют графы при анализе функционирование неких систем.
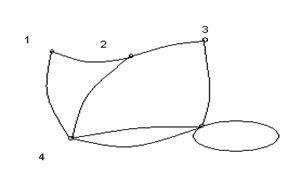
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий E, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом G = (V, E). При этом элементы множества V называются вершинами графа, а элементы множества E – ребрами. Определение. Если вершина v является концом ребра В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями (на рисунке 1.4 при вершине 5 имеется петля). Одинаковые пары в множестве E называются кратным и (или параллельными) ребрами. Количество одинаковых пар (v, w) в E называется кратностью ребра (v, w). Например, на рисунке 1.1 все рёбра имеют кратность 1, а на рисунке 1.2 есть два ребра, соединяющих одни и те же вершины 1 и 4, следовательно, их кратность равна двум. Множество V и набор E определяют граф с кратными ребрами – псевдограф. Псевдограф без петель называется мультиграфом. Если в наборе E ни одна пара не встречается более одного раза, то мультиграф называется графом. Ниже, на рисунке 1.1 изображен граф, на рисунке 1.2 мультиграф, на рисунке 1.4 – псевдограф. Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины. На рисунке 1 изображены некоторые неориентированные графы. Рисунок 1.
1.1 1.2 1.3
1.4 1.5
Замечание 1. Слово “линия”, которое мы используем, подразумевает несущественность того, какая конкретно линия используется для соединения двух вершин графа, то есть её геометрические характеристики не имеют значения. Замечание 2. Граф можно определить, также как совокупность двух множеств Определение. Если х = { v, w } – ребро графа, то вершины v, w называются концами ребра х. Определение. Если пары в наборе E являются упорядоченными, то граф называется ориентированным или орграфом. Если пишут Определение. Вершины v, w графа G = (V, E) называются смежными, если { v,w }ÎЕ. Два ребра называются смежными, если они имеют общую вершину. Определение. Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется висячей, если ее степень равна единице и изолированной, если ее степень равна нулю. На рисунке 1.5 все вершины, кроме вершины 1, являются висячими. На рисунке 1.3 вершина 4 является изолированной. Если граф состоит только из таких вершин, его называют пустым. В некоторых случаях пустым называют граф, не имеющей ни одной вершины. Рисунок 2.
2.1 2.2 2.3
a. 2.5 На рисунке 2 представлены различные типы
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.01 с.) |

 называется функция
называется функция  , где
, где  произвольное множество, а
произвольное множество, а  определённое ранее двоичное множество
определённое ранее двоичное множество  .
. местным предикатом, определённым на множестве
местным предикатом, определённым на множестве  называется двузначная функция от
называется двузначная функция от 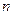 аргументов из произвольного множества
аргументов из произвольного множества  - предметными переменными. В принципе, можно определить предикат как функцию
- предметными переменными. В принципе, можно определить предикат как функцию  , то есть допустить, что переменные принимают значения из различных множеств – в некоторых случаях это оказывается удобным.
, то есть допустить, что переменные принимают значения из различных множеств – в некоторых случаях это оказывается удобным. соответствует предикат
соответствует предикат  такой, что
такой, что  тогда и только тогда, когда
тогда и только тогда, когда  ; всякий предикат
; всякий предикат  можно поставить в соответствие
можно поставить в соответствие  местный предикат
местный предикат 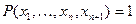 тогда и только тогда, когда
тогда и только тогда, когда  . Поскольку функция должна быть однозначной, то это соответствие требует, чтобы для любого
. Поскольку функция должна быть однозначной, то это соответствие требует, чтобы для любого  выполнялось
выполнялось 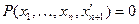 . Поэтому обратное соответствие (от предиката к функции) возможно только при выполнении указанного условия.
. Поэтому обратное соответствие (от предиката к функции) возможно только при выполнении указанного условия. , для двухместных предикатов будем пользоваться обозначениями вида
, для двухместных предикатов будем пользоваться обозначениями вида  , которые употреблялись ранее для бинарных отношений.
, которые употреблялись ранее для бинарных отношений. является двухместным предикатом, предметной областью которого могут служить любые множества действительных чисел. Высказывание
является двухместным предикатом, предметной областью которого могут служить любые множества действительных чисел. Высказывание  истинно, а высказывание
истинно, а высказывание  ложно. Если вместо одной из переменных подставить число, то получится одноместный предикат:
ложно. Если вместо одной из переменных подставить число, то получится одноместный предикат:  и так далее.
и так далее. не существует натуральных чисел
не существует натуральных чисел  , которые удовлетворяли бы равенству
, которые удовлетворяли бы равенству  . Этому равенству можно поставить в соответствие предикат
. Этому равенству можно поставить в соответствие предикат  , истинный тогда и только тогда, когда оно выполняется.
, истинный тогда и только тогда, когда оно выполняется. и
и  не станут равными или прекратить вычисление цикла после ста повторений”. Если обозначить через
не станут равными или прекратить вычисление цикла после ста повторений”. Если обозначить через  счётчик повторений, то описанное здесь условие примет вид
счётчик повторений, то описанное здесь условие примет вид  , а само указание в целом описывается выражением: “повторять, если
, а само указание в целом описывается выражением: “повторять, если 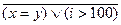 ”.
”. предикат, определённый на множестве
предикат, определённый на множестве 
 истинно” обозначается
истинно” обозначается  или
или  . Здесь множество
. Здесь множество  . Знак
. Знак  называется квантором общности.
называется квантором общности. или
или  . Знак
. Знак  называется квантором существования. Переход от предиката
называется квантором существования. Переход от предиката  не зависит от переменной
не зависит от переменной  или
или  переменная
переменная 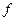 первое выражение равно определенному числу, а второе становится функцией от пределов интегрирования.
первое выражение равно определенному числу, а второе становится функцией от пределов интегрирования. чётное число”. Тогда высказывание
чётное число”. Тогда высказывание  истинно на любом множестве, содержащем хотя бы одно чётное число и ложно на любом множестве нечётных чисел.
истинно на любом множестве, содержащем хотя бы одно чётное число и ложно на любом множестве нечётных чисел. на множествах
на множествах  есть одноместный предикат от переменной
есть одноместный предикат от переменной  . Предикат
. Предикат  (можно записать
(можно записать  ) высказывание истинное на множестве, состоящем из одного элемента и ложное на всяком другом множестве. Высказывание
) высказывание истинное на множестве, состоящем из одного элемента и ложное на всяком другом множестве. Высказывание  утверждает, что в множестве
утверждает, что в множестве  утверждает, что для любого элемента
утверждает, что для любого элемента  . Последние два высказывания говорят о том, что перестановка кванторов меняет смысл высказывания и условие его истинности.
. Последние два высказывания говорят о том, что перестановка кванторов меняет смысл высказывания и условие его истинности. существует такая подстановка констант вместо всех переменных, что
существует такая подстановка констант вместо всех переменных, что  .
. является тавтологией.
является тавтологией. и
и  эквивалентны в соответствии с этим определением, то формула
эквивалентны в соответствии с этим определением, то формула  является тождественно истинной.
является тождественно истинной. . Пусть для некоторого предиката
. Пусть для некоторого предиката  , для которого
, для которого  истинно. Следовательно, для любых значений
истинно. Следовательно, для любых значений  и правая часть истинна. Если же левая часть ложна, то всегда существует
и правая часть истинна. Если же левая часть ложна, то всегда существует 
 .
. .
. ,
, .
. “
“  “
“ 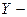 некоторое переменное выражение, не содержащее переменной
некоторое переменное выражение, не содержащее переменной  .
. .
. .
.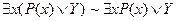 .
.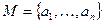 конечна, то кванторы переходят в конечные формулы логики высказываний:
конечна, то кванторы переходят в конечные формулы логики высказываний: ,
,  .
. . Тогда мощность объединения этих множеств равна сумме мощностей данных множеств:
. Тогда мощность объединения этих множеств равна сумме мощностей данных множеств: .
. способами, причём любой способ выбора элемента
способами, причём любой способ выбора элемента  способами. Это правило называется правилом суммы.
способами. Это правило называется правилом суммы. . Рассмотрим декартово произведение этих множеств
. Рассмотрим декартово произведение этих множеств  . Напомним, что элементами этого произведения будут векторы (кортежи) длины
. Напомним, что элементами этого произведения будут векторы (кортежи) длины  вида
вида  .
. .
. ) можно сделать
) можно сделать  способами. Это правило называется правилом произведения, или умножения.
способами. Это правило называется правилом произведения, или умножения. .
. .
. , в котором все элементы различны, называется размещением без повторений по
, в котором все элементы различны, называется размещением без повторений по  и равно
и равно  .
. .
. и равно
и равно  .
. , где
, где  - количество очков, выпавших на соответствующей кости. Речь идёт о перестановках с повторениями по 3 элемента из 6. Получаем:
- количество очков, выпавших на соответствующей кости. Речь идёт о перестановках с повторениями по 3 элемента из 6. Получаем:  .
. и равно
и равно  .
. .
. .
. раз, 2-й элемент -
раз, 2-й элемент -  раз и так далее. Тогда векторы длины
раз и так далее. Тогда векторы длины  и равно
и равно  .
. , получим формулу для перестановок без повторений.
, получим формулу для перестановок без повторений.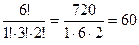 .
. . Формула для вычисления
. Формула для вычисления  . Если некоторые (или все) элементы, образующие сочетания, могут повторяться, то их называют сочетаниями повторениями. Обозначение всех сочетаний без повторений
. Если некоторые (или все) элементы, образующие сочетания, могут повторяться, то их называют сочетаниями повторениями. Обозначение всех сочетаний без повторений 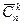 . Формула для вычисления
. Формула для вычисления  . Запоминать последнюю формулу нет необходимости.
. Запоминать последнюю формулу нет необходимости. и
и  являются различными размещениями, но обозначают одно и то же сочетание.
являются различными размещениями, но обозначают одно и то же сочетание.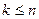 , причём в случае равенства получим естественный результат
, причём в случае равенства получим естественный результат  . Но для сочетаний с повторениями это требование необязательно, как будет видно из приведённого ниже примера.
. Но для сочетаний с повторениями это требование необязательно, как будет видно из приведённого ниже примера.
 .
. .
. и
и  ) сталкиваются ещё в школе при изучении формул сокращённого умножения:
) сталкиваются ещё в школе при изучении формул сокращённого умножения: .
.



 и
и  инцидентен ровно двум элементам
инцидентен ровно двум элементам  .
.