
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 4. Основные виды отношений.Содержание книги
Поиск на нашем сайте Из содержания предыдущей лекции и рассмотренных в ней примеров видно, что понятие “отношение” следует понимать весьма широко. В данной лекции мы попытаемся ввести определённую классификацию отношений и рассмотреть наиболее значительные с точки зрения математики виды отношений – а именно отношения эквивалентности и порядка.
Определение. Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно. Пример 1. а) Отношение равенства (часто обозначается б) Утверждения вида в) Рассмотрим множество треугольников на координатной плоскости, считая, что треугольник задан, если даны координаты его вершин. Два треугольника будем считать равными (конгруэнтными), если при наложении они совпадают, то есть, переведены друг в друга с помощью некоторого перемещения. Равенство является отношением эквивалентности на множестве треугольников. г) Отношение “иметь один и тот же остаток отделения на натуральное число е) Отношение “быть делителем” не является на множестве Пусть на множестве Эта система обладает следующими свойствами: 1) она образует разбиение множества 2) любые два элемента из одного класса эквивалентны; 3) любые два элемента из разных классов не эквивалентны. Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы Построенное разбиение, то есть система классов – подмножеств множества Пример 2. а) Все классы эквивалентности по отношению равенства б) Формулы, описывающие одну и ту же элементарную функцию, находятся в одном классе эквивалентности по отношению равносильности. В данном случае счётными являются само множество формул, множество классов эквивалентности (то есть индекс разбиения) и каждый класс эквивалентности. в) Разбиение множества треугольников по отношению равенства имеет континуальный индекс, причём каждый класс имеет также мощность континуум. г) Разбиение множества натуральных чисел по отношению “иметь общий остаток при делении на 7” имеет конечный индекс 7 и состоит из семи счётных классов.
Определение 1. Отношение Определение 2. Отношение Оба типа отношений вместе называются отношениями порядка. Элементы Пример 3. а) Отношения “ б) Определим отношения “ 1) 2) Тогда, например, в) На системе подмножеств множества г) Отношение подчинённости в трудовом коллективе создаёт строгий частичный порядок. В нём, например, несравнимыми являются сотрудники различных структурных подразделений (отделов и т. п.). д) В алфавите русского языка порядок букв зафиксирован, то есть всегда один и тот же. Тогда этот список определяет полное упорядочение букв, которое называется отношением предшествования. Обозначается Пример 4. а) Наиболее известным примером лексикографического упорядочения слов является упорядочение слов в словарях. Например, б) Если рассматривать числа в позиционных системах счисления (например, в десятичной системе) как слова в алфавите цифр, то их лексикографическое упорядочение совпадает с обычным, если все сравниваемые числа имеют одинаковое количество разрядов. В общем же случае эти два вида могут не совпадать. Например, в) Лексикографическое упорядочивание цифровых представлений дат вида 19.07.2004 (девятнадцатое июля две тысячи четвёртого года) не совпадает с естественным упорядочением дат от более ранних к более поздним. Например, дата 19.07.2004 “лексикографически” старше восемнадцатого числа любого года. Чтобы возрастание дат совпадало с лексикографическим упорядочением, обычное представление надо “перевернуть”, то есть записать в виде 2004.07.19. так обычно делают при представлении дат в памяти ЭВМ.
Назад, в начало конспекта.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы
) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы  или
или  , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “
, состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “  ”.
”.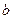 ” на множестве натуральных чисел является отношением эквивалентности.
” на множестве натуральных чисел является отношением эквивалентности.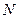 отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже). задано отношение эквивалентности
задано отношение эквивалентности  . Осуществим следующее построение. Выберем элемент
. Осуществим следующее построение. Выберем элемент  и образуем класс
и образуем класс  (подмножество
(подмножество  и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент
и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс
и образуем класс  , состоящий из
, состоящий из  и эквивалентных ему элементов. Продолжая эти действия, получим систему классов
и эквивалентных ему элементов. Продолжая эти действия, получим систему классов  (возможно, бесконечную) такую, что любой элемент из множества
(возможно, бесконечную) такую, что любой элемент из множества  .
. . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
. Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства. сравнимы по отношению порядка
сравнимы по отношению порядка  или
или  . Множество
. Множество  ” и “
” и “  ” являются отношениями нестрогого порядка, отношения “<” и “>” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества
” являются отношениями нестрогого порядка, отношения “<” и “>” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества  следующим образом:
следующим образом: , если
, если  ;
; , если
, если  координаты выполняется
координаты выполняется  .
. , но
, но  и
и 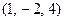 несравнимы. Таким образом, эти отношения частично упорядочивают
несравнимы. Таким образом, эти отношения частично упорядочивают  ” задаёт нестрогий частичный порядок, а отношение строгого включения “
” задаёт нестрогий частичный порядок, а отношение строгого включения “  ” задаёт строгий частичный порядок. Например,
” задаёт строгий частичный порядок. Например,  , а
, а  и
и  не сравнимы.
не сравнимы. (
( предшествует
предшествует  ). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.
). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением. (так как
(так как  ), поэтому слово лес расположено в словаре раньше слова лето.
), поэтому слово лес расположено в словаре раньше слова лето. и
и  , но
, но  , а
, а  . Для того, чтобы они совпадали, нужно уравнять число разрядов у всех сравниваемых чисел, приписывая слева нули. В данном примере при этом получим
. Для того, чтобы они совпадали, нужно уравнять число разрядов у всех сравниваемых чисел, приписывая слева нули. В данном примере при этом получим 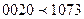 . Такое выравнивание происходит автоматически при записи целых чисел в ЭВМ.
. Такое выравнивание происходит автоматически при записи целых чисел в ЭВМ.


