
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция № 16. Некоторые классы графов и их частей.Содержание книги
Поиск на нашем сайте
Определение. Связный неориентированный граф без циклов называется неориентированным деревом или просто деревом. Из определения следует, что дерево не может содержать ни петель, ни кратных рёбер. Определение. Несвязный неориентированный граф без циклов называется лесом; связные компоненты леса являются деревьями. Очевидно, что люба часть дерева или леса также не имеет циклов. В таком графе любая цепь является простой – в противном случае, она содержала бы цикл. Теорема 16.1. Любые две вершины дерева связаны одной и только одной цепью. Обратно, если две любые вершины графа можно связать только одной цепью, то он является деревом. Определение. Вершина Если конечное дерево состоит более чем из одной вершины, оно имеет хотя бы две концевые вершины и хотя бы одно концевое ребро. Пусть в дереве В нём все рёбра имеют направление от корня (см. рисунок 1). Рисунок 1.
Если же изменить направления всех рёбер ориентированного дерева на противоположные (к корню), то получится ориентированный граф, который называется сетью сборки. В общем случае, такой граф тоже является ориентированным деревом. В каждую вершину ориентированного дерева, за исключением корня, входит только одно ребро. Иначе говоря, эта вершина является концом только одного ребра. Отсюда прямо следует, что в конечном дереве число вершин на один превышает число рёбер. Замечание. Любое дерево можно ориентировать, выбрав в качестве корня любую его вершину. Пусть дано конечное дерево Далее удалим из дерева все вершины типа 1 и инцидентные им рёбра. Останется связный граф Легко видеть, что в конечном дереве имеются лишь вершины конечного числа типов, причём число вершин максимального типа равно одному или двум, так как в соответствующем дереве каждая вершина является концевой. Теорема 16.2. Центрами дерева являются вершины максимального типа и только они. Из данной теоремы прямо следует, что дерево имеет либо один, либо два центра. Диаметральные цепи в деревьях проходят через центр дерева, либо, если их два, через оба центра. В первом случае длина диаметральной цепи равна Определение. Цикломатическим числом конечного неориентированного графа Цикломатическое число дерева равно нулю. Цикломатические числа остальных конечных графов положительны.
Понятие ориентированного графа (орграфа) было определено ранее. Сейчас рассмотрим подробнее, как выглядят в таком графе пути и циклы. Пусть дан ориентированный граф Дадим определение пути в ориентированном графе. Сразу оговоримся, что это понятие можно определять различными способами; мы приводим только один. Определение. Путь из вершин и рёбер – это такая последовательность рёбер и вершин графа Путь, состоящий из одной вершины, имеет нулевую длину. Каждому пути Определение. Путь Начало цикла обычно не фиксируется, иначе говоря, все пути, получающиеся друг из друга циклическими сдвигами – это один и тот же цикл. Определение простого ориентированного цикла аналогично соответствующему определению для неориентированного цикла – это цикл, в котором каждая вершина инцидентна ровно двум его рёбрам. Любой граф, содержащий циклы, можно “укоротить” до простого. Граф, не содержащий циклов, называется ациклическим. Определение. Вершина ориентированного графа называется начальной, если в неё ни входит ни одно ребро и конечной, если из неё не выходит ни одно ребро. Во всяком ациклическом графе есть хотя бы одна начальная и хотя бы одна конечная вершина. Максимальным рангом Пусть вершины конечного ориентированного графа пронумерованы от 1 до Понятия длины путей, протяжённости и расстояния между вершинами определяются для ориентированного графа так же, как для неориентированного графа.
Нередко приходится иметь дело с различиями между вершинами графа. Тогда их разбивают на классы. Каждый класс состоит из вершин, имеющих обще свойство. Примером таких свойств могут быть следующие из уже описанных ранее свойств: иметь данную степень, иметь данное расстояние от корня, иметь данный ранг и так далее. В других случаях разбиение определяется свойствами объектов, описываемых при помощи графа. Например, структурная формула химического соединения – это граф, в котором вершины соответствуют атомам, рёбра – валентным связям, а классы состоят из вершин, соответствующих атомам одного и того же элемента. Пусть дано разбиение графа на классы (всё равно, по какому признаку). Каждой вершине можно соотнести метку, указывающую, какому именно классу она принадлежит. Такая вершина называется помеченной. Метки являются элементами заданно множества. Иногда они явно указывают на свойства, определяющие классы: например, степени, ранги вершин, и их расстояния от корня можно метить соответствующими числами. Однако часто абстрагируются от конкретного характера отличий между вершинами, и тогда метки указывают только на сам факт сходства вершин или их различия. Соотнесение таких меток вершинам называют раскраской их в разные цвета. Аналогичным образом говорят о раскраске рёбер графа и вообще о раскраске элементов произвольного множества.
Назад, в начало конспекта.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.01 с.) |

 называется концевой или висячей вершиной графа
называется концевой или висячей вершиной графа 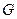 , если её степень равна единице. Ребро, инцидентное концевой вершине, также называется концевым.
, если её степень равна единице. Ребро, инцидентное концевой вершине, также называется концевым. ребра
ребра  можно соединить с корнем единственной простой цепью. Если эта цепь не содержит ребра
можно соединить с корнем единственной простой цепью. Если эта цепь не содержит ребра  к
к 
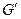 , также являющийся деревом. Дерево
, также являющийся деревом. Дерево  , во втором -
, во втором - 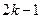 , где
, где  максимальный тип дерева.
максимальный тип дерева. . Здесь
. Здесь  количество связных компонентов графа,
количество связных компонентов графа,  количество рёбер,
количество рёбер,  количество вершин.
количество вершин. . Каждое ребро имеет начало
. Каждое ребро имеет начало  и конец
и конец 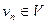 ; также говорят, что данное ребро выходит из вершины
; также говорят, что данное ребро выходит из вершины 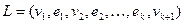 , в которой вершина
, в которой вершина 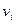 является началом
является началом  го ребра, а вершина
го ребра, а вершина  его концом. Вершина
его концом. Вершина 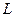 , вершина
, вершина  его концом, число рёбер
его концом, число рёбер  рёбер этого пути. Её называют путём из рёбер. Такое понятие пути – аналог соответствующего понятия для неориентированного графа. Наконец, для графа, не содержащего кратных рёбер, можно указать взаимнооднозначное соответствие с последовательностью
рёбер этого пути. Её называют путём из рёбер. Такое понятие пути – аналог соответствующего понятия для неориентированного графа. Наконец, для графа, не содержащего кратных рёбер, можно указать взаимнооднозначное соответствие с последовательностью  вершин пути. В зависимости от ситуации удобнее использовать тот или иной способ обозначения пути.
вершин пути. В зависимости от ситуации удобнее использовать тот или иной способ обозначения пути. вершины ориентированного графа называется максимальная из длин путей этого графа с концом в вершине
вершины ориентированного графа называется максимальная из длин путей этого графа с концом в вершине  .
.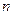 . Нумерация вершин называется правильной на ребре
. Нумерация вершин называется правильной на ребре  , если
, если  и правильной на графе
и правильной на графе 


