
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условный экстремум, функция Лагранжа. Наибольшее и наименьшее значения функции в замкнутой ограниченной области.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поиск условного экстремума осуществляется с помощью ф.Лагранжа
1) Необходимое условие существования условного экстремума
2) Достаточное условие существования условного экстремума
18. Первообразная и неопределенный интеграл, их свойства. Таблица основных интегралов. Основные приемы интегрирования: интегрирование методом разложения, замена переменной, интегрирование по частям. Разложение дробной рациональной функции на простейшие дроби. Интегрирование простейших дробей. Интегрирование рациональных дробей. Функция F (x) называется первообразной для функции f (x) на некотором промежутке, если в каждой точке этого промежутка функция F (x) дифференцируема и выполняется равенство F '(x) = f (x). Множество всех первообразных для данной функции f (x) на интервале (a; b) называется неопределённым интегралом функции f(x) на этом интервале и обозначается символом:
Свойства неопределённого интеграла
Таблица основных интегралов.
Основные приемы интегрирования Метод разложения: По 4 свойству – разбить на сумму интегралов
Интегрирование дробей
1. Если степень числителя больше или равна степени знаменателя, то дробь неправильная и нужно поделить уголком, тем самым выделив целую часть:
2. Знаменатель разложить на множители и привести всю дробь к сумме простых дробей: I. II. III. а) б) Разложить знаменатель на множители и решать, используя пределы Ао, Во. Интегрирование тригонометрии 1. Интегралы вида ∫cos(m*(x))sin(n*(x))dx находят в зависимости от четности степеней m и n следующим образом: а) если m или n нечетное, то используют замену переменной: t=sinx, при нечетном m; t=cosx, при нечетном n, и формулу sin2x+cos2x=1; б) если m и n четные, то используют формулы понижения степени:
в) Если m+n=−2k, k∈N т. е. m+n является целым четным отрицательным числом, то удобно использовать подстановки tgx=t и ctgx=t. 2. Интегралы вида ∫sin(m*(x))cos(n*(x))dx, ∫cos(m*(x))cos(n*(x))dx, ∫sin(m*(x))sin(n*(x))dx вычисляют с помощью преобразований подынтегральной функции по следующим формулам:
sin(m*(x))cos(n*(x))dx = sin(m*(x))sin(n*(x))dx = cos(m*(x))cos(n*(x))dx = 4. Интегралы вида, R(sinx,cosx)dx где R(u,v)− рациональная функция двух переменных, приводят к интегралам от рациональных функций нового аргумента t подстановкой t=tg(x/2). При этом используются формулы
Если под интегралом sinx и cosx содержатся только в четных степенях, то удобнее использовать подстановку tgx=t.
Интегрирование иррациональности
Определенный интеграл как предел интегральной суммы. Основные свойства. Т. о среднем. Определенным интегралом от f(x) на [a,b] называется предел интегральных сумм при n стремящемся к бесконечности.
Т. о среднем. Если функция f (x) непрерывна на отрезке [ a;b ], то на этом отрезке найдётся хотя бы одна точка c, в которой выполняется равенство:
Производная интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница. Замена переменной в определенном интеграле и интегрирование по частям. Пусть функция y = f (x) непрерывна на отрезке [ a;b ]. Тогда она непрерывна на отрезке [ a;x ] для любого xÎ [ a;b ]. Следовательно, на отрезке [ a;b ] определена функция Свойства этой функции сформулируем в виде теоремы. Теорема. Пусть функция f (x) непрерывна на отрезке [ a;b ]. Тогда функция 1) непрерывна на отрезке [ a;b ]; 2) имеет производную F' (x) в каждой точке x Î[ a;b ], удовлетворяющую равенству Формула Ньютона–Лейбница Теорема. Пусть функция f (x) непрерывна на отрезке [ a;b ] и F(x) – какая-либо её первообразная на отрезке [ a;b ]. Тогда определённый интеграл от функции f (x) по отрезку [ a;b ] равен разности значений функции F(x) в точках b и a:
Замена переменной в определённом интеграле Теорема. Пусть функция f (x) непрерывна на отрезке [ a;b ] и пусть функция x = j(t) имеет непрерывную производную j'(t) на отрезке [a;b], область значений этой функции – отрезок [ a;b ], т.е. a £ j (t) £ b для t Î [a;b], причём j(a) = a, j(b) = b. Тогда справедливо равенство:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.76.238 (0.009 с.) |


 Решая систему, находим стационарные точки и параметр функции
Решая систему, находим стационарные точки и параметр функции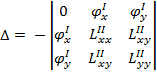
 (Mo) < 0 – точка условного максимума
(Mo) < 0 – точка условного максимума
 .
.
 .
.



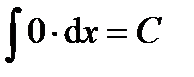 .
.
 .
.
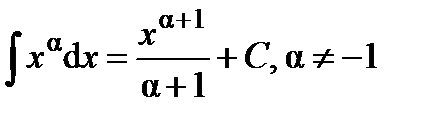 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.


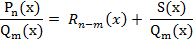
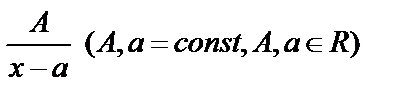 ,
, ,
, )D < 0
)D < 0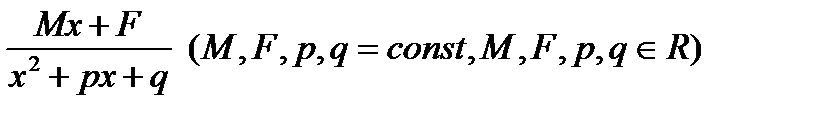 D > 0
D > 0

 ,
, .
.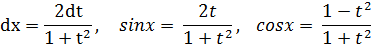






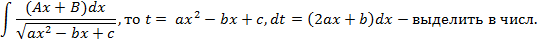


 , которая называется интегралом с переменным верхним пределом.
, которая называется интегралом с переменным верхним пределом.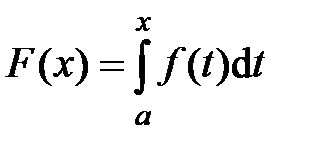 обладает свойствами:
обладает свойствами: .
.
 .
.


