
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Падение частицы на потенциальный барьер конечной ширины. Туннельный эффект.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Коэфициент В2 и А2А3 в 3-ей области (тоесть не от чего не отражаеться) Квантовый гармонический осциллятор. Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д. Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси где
Гармонический осциллятор играет также важную роль в описании ансамбля одинаковых частиц, находящихся в одном и том же квантовом состоянии (бозоны). Это связано с тем, что энергетические уровни гармонического осциллятора эквидистантны, и разделяющий два соседних уровня интервал энергии равен ћw. При этом любому уровню энергии, определенному целым числом n (т.е. отстоящему на расстоянии nћw от основного уровня), можно сопоставить ансамбль, состоящий из n одинаковых частиц (или квантов), каждая из которых имеет энергию ћw. Переход осциллятора с уровня n на уровень n+1 или n-1 соответствует рождению или уничтожению кванта энергии ћw 17) Энергетический спектр и волновые функции операторов квантового гармонического осциллятора.
Собственные значения и собственные волновые функции операторов М и М.
Атом водорода.
Распишем это уравнение
Энергетический спектр и волновые функции атома водорода.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.138.13 (0.01 с.) |

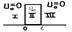


 ,
,  -коэф.прохожд.барьера,частица может пройти барьер непреодалевая его при
-коэф.прохожд.барьера,частица может пройти барьер непреодалевая его при  -тунельный ефект.Т.К.ур-ние Шреде.для1 и для 3-ей области одинаковы,то поле барьера энергии частицы такоеже как и до барьера.При прохожд.через барьер она не тратит энерг.-тун.эфект.Тунель.Эфе.процесс прох.частицы при
-тунельный ефект.Т.К.ур-ние Шреде.для1 и для 3-ей области одинаковы,то поле барьера энергии частицы такоеже как и до барьера.При прохожд.через барьер она не тратит энерг.-тун.эфект.Тунель.Эфе.процесс прох.частицы при  под действием возвращающей квазиупругой силы
под действием возвращающей квазиупругой силы  . Потенциальная энергия такого осциллятора имеет вид
. Потенциальная энергия такого осциллятора имеет вид 
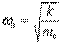 - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.
- собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.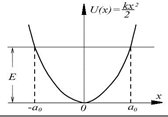
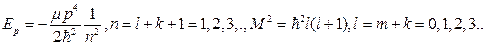
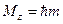
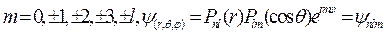 -главное орбитальное состояние, n-главное квантовое число,M-орбитальный механический момент,l-орбит.квант.число.m-магнит.квантовое число
-главное орбитальное состояние, n-главное квантовое число,M-орбитальный механический момент,l-орбит.квант.число.m-магнит.квантовое число 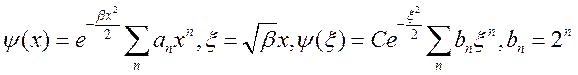
 -уровни энергии.
-уровни энергии. 
 Энергия осциллятора - дискретная имеет бесконечно много уров.которые наход.на один.растоя.друг от друга
Энергия осциллятора - дискретная имеет бесконечно много уров.которые наход.на один.растоя.друг от друга  При
При  дискретность исчезает Энергет.спектр.одномер.квант.осцилят. - не вырожд.У реаль.трехмер.осцилят.если они изотропны
дискретность исчезает Энергет.спектр.одномер.квант.осцилят. - не вырожд.У реаль.трехмер.осцилят.если они изотропны 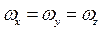 наступает вырожд.
наступает вырожд.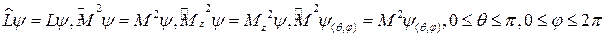
 орбит.квант.число l=k+m
орбит.квант.число l=k+m  -мех.момент квантовой часитцы дискрет.
-мех.момент квантовой часитцы дискрет. 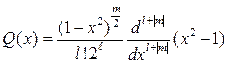 -полином Лагранжа
-полином Лагранжа 
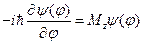 ,
, 
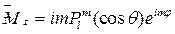 -опер.мв2 и мз комутируют между
-опер.мв2 и мз комутируют между 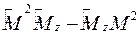
 собой
собой 1) Помест.ядро в начало коорд. 2) Будем считать, что маса ядра значит. больше массы элект; ядро неподвиж.. Это позволяет раздел.ядерную и электрон. подсистемы и рассматр.только движ.электрона. 3) Будем считать заряд электр.тонечным, который подчиняется закону Кулона:
1) Помест.ядро в начало коорд. 2) Будем считать, что маса ядра значит. больше массы элект; ядро неподвиж.. Это позволяет раздел.ядерную и электрон. подсистемы и рассматр.только движ.электрона. 3) Будем считать заряд электр.тонечным, который подчиняется закону Кулона:  ;
; 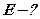
 Исполь.стац. Ур. Шредингера
Исполь.стац. Ур. Шредингера Запишем это ур. в системе единиц Хартри: ед. массы- масса электрона, ед. заряда – заряд электрона, ед. действия – постоянная Планка.
Запишем это ур. в системе единиц Хартри: ед. массы- масса электрона, ед. заряда – заряд электрона, ед. действия – постоянная Планка. 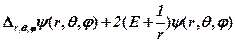 .
. ;
; 

 Зная то решение правой части имеет вид:
Зная то решение правой части имеет вид: 
 ;
; , где
, где  орбитальное квантовое число. Момент имеет проекции:
орбитальное квантовое число. Момент имеет проекции:  ,
,  ; запишем
; запишем  , (:
, (:  )
) 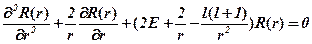 . Коэффициенты обращаются в бесконечность при
. Коэффициенты обращаются в бесконечность при  эти точки надо подавить при нахождении волн. ф-ии
эти точки надо подавить при нахождении волн. ф-ии  . Потенциальная энергия взаимодействия эл-на с ядром уменьшается с удалением от ядра и стремится к некоторой постоянной
. Потенциальная энергия взаимодействия эл-на с ядром уменьшается с удалением от ядра и стремится к некоторой постоянной  , при
, при  . Решение сильно зависит о того что
. Решение сильно зависит о того что 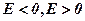 :
:  (*);
(*); 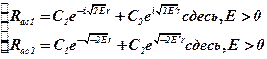 точное решение будем искать в
точное решение будем искать в  ,
,  -для подавления особых точек уравнения. Из анализа поведения ф-ии вытекает, что
-для подавления особых точек уравнения. Из анализа поведения ф-ии вытекает, что  . Найдем 1 и 2 производную и подставим в ур.. (*) и пол ур.
. Найдем 1 и 2 производную и подставим в ур.. (*) и пол ур. 
 . Получим ур. Относительно членов ряда
. Получим ур. Относительно членов ряда  . Это ур. может выполняться, только если все коеф-ты при
. Это ур. может выполняться, только если все коеф-ты при  равно нулю. Найдем коеф. При
равно нулю. Найдем коеф. При  :
: 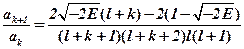 ряд не сходится, чтобы сошлось, надо оборвать ряд.
ряд не сходится, чтобы сошлось, надо оборвать ряд. 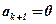
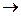
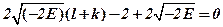
 , значит
, значит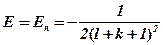 , где
, где  - главное квантовое число,
- главное квантовое число, 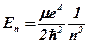 ,
,  , где
, где 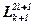 - полином Лабера
- полином Лабера 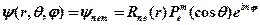 , Состояние задаваемое с квантовими числами наз. атомной орбиталью
, Состояние задаваемое с квантовими числами наз. атомной орбиталью


