
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Качественная картина атома гелия.Содержание книги Поиск на нашем сайте
Пренебрежем спин орбитальным взаимодействием:
Теперь пренебрежем спин-спиновым взаимодействием:
2)
Расчет атома гелия методом теории возмущений.
1) 2) Невозмущенному уровню енергии соответствует 2 волновые функции, тесть двухкратно вироджений(обменное вырождение) Для расчета применим теор возмущ. для вироджений:
Возмущенной системи в Н представлениях
Подставив в нашу систему +A и –А мы получем:
Обменный интеграл, обменная энергия.
По скольку электрон в атоме представляет собой заряженное облако, то
Энергия взаимодействия двух облаков –это кулоновское взаимодействие, однако при антипаралельной ориентации спинов часть энергии имеет знак -, что означает притяжение этих облаков.Электроны при перекрытии волновых ф-ии обмениваются между собой состояниями и время етого процесса:
Электронная подсистема легкая, ядерная -тяжелая.Позволяет разделить систему на
Енергия эл. Подсистемы будет зависить от энергии взаимодействия ядер, как от параметра.Стационарное уравнение Шредингера:
1) Вкачестве невозмущенной системы принемается система с безконечно удаленними ядрами. Тога получим:
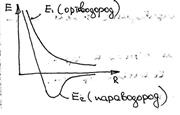
Такая запись справедлива только корда И енергия имет вид Так как волновая функция не ортогональная и не ортонормированая то Ортоводород параводород
Молекула образуется только в том случае сумарний спин рамен 0.
Обменная енергия есть следствием квантових ефектов.
43) Уравнение Шредингера для твердого тела.
44) Движение электрона в периодическом потенциальном поле решетки. Так как атомы расположены периодически то электрон будет изменять свою энергию также периодически:
Потенциальная энергия периодическая
Поскольку функция
При решении системы уравнений
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.37.200 (0.006 с.) |





 ;
; 


 ;
; 

 -имеют не определенные значения;
-имеют не определенные значения; 
 Возможна еще одна функция
Возможна еще одна функция 
 Гелий разбивается на два класса: 1)
Гелий разбивается на два класса: 1)  Проведем расчет этого уравнения методом возмущений:
Проведем расчет этого уравнения методом возмущений: 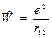 (возмущение); Невозмущенное состояние:
(возмущение); Невозмущенное состояние: 



 Совокупность представляет собой волновую функцию
Совокупность представляет собой волновую функцию

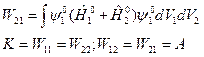

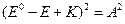


 Общая функция представляет собой произведение координатной функ на спиновую:
Общая функция представляет собой произведение координатной функ на спиновую: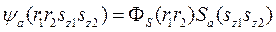 парагелий
парагелий 
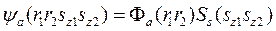 ортогелий
ортогелий 



 Можно рассматривать как среднюю плотность эл заряда точки
Можно рассматривать как среднюю плотность эл заряда точки 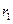 для электрона, находящегося в ином состоянии.
для электрона, находящегося в ином состоянии.  второй электрон
второй электрон  представляет собой кулоновскую энергию взаимодействия двух электронных облаков.
представляет собой кулоновскую энергию взаимодействия двух электронных облаков. 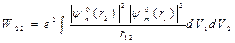
 (кулоновские интегралы)
(кулоновские интегралы)
 -срд. Плотность эл заряда в точке r,когда частью своей електрон находится в нном состоянии, частью в мном состоянии
-срд. Плотность эл заряда в точке r,когда частью своей електрон находится в нном состоянии, частью в мном состоянии  ,
, 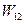 -энергия кулоновского взаимодействия двух електронов из которых находится частью в нном,частью в ммном состоянии. Это случай перекритих ф-ий електронов
-энергия кулоновского взаимодействия двух електронов из которых находится частью в нном,частью в ммном состоянии. Это случай перекритих ф-ий електронов

 - обменные интегралы
- обменные интегралы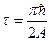
 42) Молекула водорода.
42) Молекула водорода. и
и 
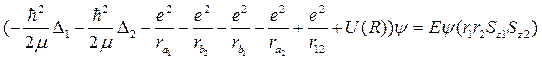
 Возможно два решения:
Возможно два решения:

 (далее смотри атом гелия)
(далее смотри атом гелия) 2)
2)
 . Корда ми начинаемс ближать ядра изменняюися волновие функции тогда
. Корда ми начинаемс ближать ядра изменняюися волновие функции тогда 


 -степень не ортогональности.Решение возможно только в том случае, если правая часть ортогональна к волновим ф-ям. Тогда получится
-степень не ортогональности.Решение возможно только в том случае, если правая часть ортогональна к волновим ф-ям. Тогда получится 

 A-ето обменный интеграл.
A-ето обменный интеграл.
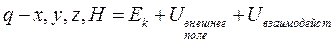
 -ур.Шреденгера для системы многих частиц,если относ.скорость частиц <<C(взаимод.мгновенное)
-ур.Шреденгера для системы многих частиц,если относ.скорость частиц <<C(взаимод.мгновенное)
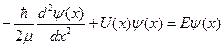
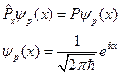


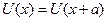 периодическая то ее мона разложить в ряд Фурэ
периодическая то ее мона разложить в ряд Фурэ
 В результате получаем уравнение
В результате получаем уравнение  (*) которое представляет собой уравнение Шредингера для электрона, в Р-представлении. Данное уравнение обладает тем свойством,что в него входят такие
(*) которое представляет собой уравнение Шредингера для электрона, в Р-представлении. Данное уравнение обладает тем свойством,что в него входят такие  аргументы отключающиеся друг от друга на величину
аргументы отключающиеся друг от друга на величину 
 ,где м-целое число.
,где м-целое число. мы получим бесконечное число решений
мы получим бесконечное число решений 

 E периодически зависит от вектора к
E периодически зависит от вектора к 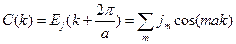 в ряд входят как косинуси так и синуси но ми оставляем только косинусы.Решыв последнее уравнение мы найдем совокупность корней
в ряд входят как косинуси так и синуси но ми оставляем только косинусы.Решыв последнее уравнение мы найдем совокупность корней  потом подставим каждий из них в систему уравнений (*) и решив ее ми получим:
потом подставим каждий из них в систему уравнений (*) и решив ее ми получим:  -функция Блоха(периодическая)
-функция Блоха(периодическая)


