
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статическое толкование волн де Бройля.Содержание книги Поиск на нашем сайте
Волновая функция, её свойства (конечность, однозначность, непрерывность). Вероятность Местонахождения частицы.
Поскольку мы вкладываем в 4)Принцип суперпозиции состояний. Если система находиться в состояниях Соотношение неопределенностей Гейзенберга. Для квантовой частицы Операторная форма квантовой механики. Оператор - это символ, который показывает, каким образом один класс функций сопоставляется другому. Выражает действия 7) Вычисление средних значений физических величин в квантовой механике. х-случ.вел. F(x).f(x)-функция распределения вероятнотси,
В квантовой механики выбирают только такие состояния в которых среднее квадрат.отклонение 0.
Собственные значения и собственные волновые функции операторов, их физический смысл.
Операторы, координаты и импульсы микрочастиц.
Для того чтоб получить оператор любой физ.величины нужно выразить ее через коорлинаты и импульс и заменить их на их операторы. Операторы момента импульса, проекции момента импульса.
Операторы энергии, гамильтолиан.
Уравнение Шредингера. Позволяет рассчитать физические величины для частиц в этом ансамбле в данный момент времени и позволяет найти значение этих величин в любой последующий момент времени
Стационарное ур. Шредингера.
Частица в потенциальной яме, квантовые энергии.
Падение частицы на барьер бесконечной ширины.
B2=0-у частицы нет причин отражаться если она попала во вторую область.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.005 с.) |


 -трехмерная волновая функция.
-трехмерная волновая функция.  -вероятность местонахождения частицы.
-вероятность местонахождения частицы. - условие нормировки.
- условие нормировки.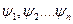 то она может находиться и в более сложном состоянии, представляющее собой суперпозицию простых состояний.
то она может находиться и в более сложном состоянии, представляющее собой суперпозицию простых состояний.  ,,,,
,,,,  - амплитуда частных состояний.
- амплитуда частных состояний. 
 - импульс является ф-цией длины волны и несвязан с координатой
- импульс является ф-цией длины волны и несвязан с координатой  . Так как пакет волн Д.Б. обладает дисперсией, то пакет волн с течением времени расплывается
. Так как пакет волн Д.Б. обладает дисперсией, то пакет волн с течением времени расплывается  . В квантовых ансамблях осуществляется только такие состояния, при которых нельзя измерить одновременно координату и импульс
. В квантовых ансамблях осуществляется только такие состояния, при которых нельзя измерить одновременно координату и импульс  ,
,  ,
,  - в квантовых ансамблях, чем точнее мы будем измерять энергию, тем больше проводить измерений.
- в квантовых ансамблях, чем точнее мы будем измерять энергию, тем больше проводить измерений. . Действует на функцию справа и не дейтсует на функцию слева
. Действует на функцию справа и не дейтсует на функцию слева  . В квантовой механики применяются только линейные и самосопряженные (эрмитовые) операторы.
. В квантовой механики применяются только линейные и самосопряженные (эрмитовые) операторы. 
 - лин.опер.-дейтсв.опер. на супер поз.ф-ций =сумме действ. На кажд.функ.отдел.Самосопр.-
- лин.опер.-дейтсв.опер. на супер поз.ф-ций =сумме действ. На кажд.функ.отдел.Самосопр.- 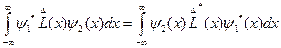

 -выч.среднего!
-выч.среднего! 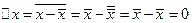 ,
, 
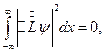
 -ур-ние по нахожд.собст.знач и собсьв.волновых функций оператора.
-ур-ние по нахожд.собст.знач и собсьв.волновых функций оператора. -ур-ние по нахожд.собст.знач и собсьв.волновых функций оператора.Как правило это лин.диф.уравн.Решение ЛДР возможно не при любых знач.параметра L,а при опред.
-ур-ние по нахожд.собст.знач и собсьв.волновых функций оператора.Как правило это лин.диф.уравн.Решение ЛДР возможно не при любых знач.параметра L,а при опред.  собственные значен.опер.
собственные значен.опер.  и только такие возмож.значения физ.величины L,изображаемой опер.
и только такие возмож.значения физ.величины L,изображаемой опер.  -вероят.обнар.физ.велич.Собст.волнов.ф-ции опер.ортонормированы,ортогональны и образ.полную ситст.ф-ций:это озн.что
-вероят.обнар.физ.велич.Собст.волнов.ф-ции опер.ортонормированы,ортогональны и образ.полную ситст.ф-ций:это озн.что  любую другую ф-цию,задданн. В этой же области простр.можно разложить по собст.волнов.ф-циям опер.L
любую другую ф-цию,задданн. В этой же области простр.можно разложить по собст.волнов.ф-циям опер.L  ,
,  К собств.волновм.функциям пред.требования:-конечность,-однозначность,-ортонормировка,-ортогональность,-полнота системы.
К собств.волновм.функциям пред.требования:-конечность,-однозначность,-ортонормировка,-ортогональность,-полнота системы.


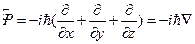 ,
,  ,
, 
 -оператор Лапласа
-оператор Лапласа ,,
,, 
 -анологично для y,z.
-анологично для y,z. 
 в сферической ситстеме координат
в сферической ситстеме координат  получим
получим  тогда
тогда  и
и 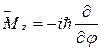
 -гамильтониан
-гамильтониан  ,
,  где
где 
 тогда запишем
тогда запишем 
 подчин. следующим уравнением:
подчин. следующим уравнением:
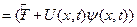
 - решение зависит от вида потенциальной энергии.
- решение зависит от вида потенциальной энергии. -во многих случаях потен.енерг.является ф-цией координат и не завистит от времени
-во многих случаях потен.енерг.является ф-цией координат и не завистит от времени  ,
, 
 ,
,  ,
, 
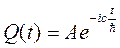 ,
, 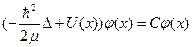 ,
, 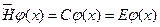 где
где  - энер.спектр системы собств знач.опер.
- энер.спектр системы собств знач.опер. 
 Для одном.ямы
Для одном.ямы  Из усл.непрерывности-
Из усл.непрерывности-  тогда
тогда 
 ,
,  ,
,  -у каждого уровня энергии есть лишь 1 волн.фу.-такой спектр не вырожд.
-у каждого уровня энергии есть лишь 1 волн.фу.-такой спектр не вырожд.  Для трех.ямы
Для трех.ямы 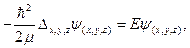


 ,
, 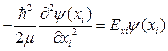
 ,
,  ,
,  -то спектр вырожден.
-то спектр вырожден. ,
,  Степень вырождения завистит от симетрии задачи,чем она выше тем выше вырожд. Если
Степень вырождения завистит от симетрии задачи,чем она выше тем выше вырожд. Если  ,то яма незах.частицу.
,то яма незах.частицу. для класич.частицы E>Uo-продал.барьер E<Uo-не прод. отражается. Для квантовой частицы 1)
для класич.частицы E>Uo-продал.барьер E<Uo-не прод. отражается. Для квантовой частицы 1) 
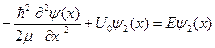 ,
, 
 -коеф.отражения от барьера.
-коеф.отражения от барьера.  -коеф.прохожд.R+D=1-достоверное событие.
-коеф.прохожд.R+D=1-достоверное событие.


