
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободная и связанная энергияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Выясним еще один физический смысл энтропии, как меру «обесцененности» энергии. Рассмотрим обратимое расширение газа при постоянной температуре (с теплообменом). Согласно первому началу термодинамики: dQ = dU+dA Второе начало можно представить dS = dQ/T Þ dQ = TdS Объединяя выражения, получим TdS = dU + dA Так как Т – постоянна, то dA= –d(U–TS). Полученное выражение показывает, что в работу переходит лишь (U–TS) часть внутренней энергии, которая называется свободной энергией и обозначается
Внутренняя энергия TS не может перейти в работу. Эта часть энергии называется связанной энергией. Она как бы обесценивается с точки зрения возможности превращения этой части внутренней энергии в механическую работу. Чем больше энтропия, тем больше «обесцененная» часть энергии. В этом смысле энтропию называют мерой «обесценивания» энергии.
Теория метода В данной работе рассматривается изменение энтропии при плавлении олова. Процесс плавления олова можно рассматривать в два этапа: I –нагревание от комнатной температуры Тк до температуры плавления Т п, II – плавление. Изменение энтропии на первом этапе можно определить:
Изменение энтропии на втором этапе:
Полное изменение энтропии равно:
Для определения изменения энтропии необходимо определить температуру плавления олова. Эту температуру определяют из условия, что при плавлении температура не изменяется. Постоянная температура при плавлении обусловлена тем, что теплота, поступающая от нагревателя, расходуется не на повышение температуры олова (т.е. не на увеличение кинетической энергии атомов в кристаллической решетке), а на разрушение кристаллической решетки. И пока существует хотя бы одна атомарная связь, температура олова не повысится. Поэтому, если снимать зависимость температуры нагрева олова от времени, то обнаружим, что некоторое время температура не изменяется. Это и есть температура плавления олова.
Описание эксперимента
Включите нагреватель и термометр (рис.3). Нагрев вести до температуры, заданной преподавателем включите секундомер и начните заполнять табл. 1.
Таблица 1
Определив из таблицы температуру плавления и воспользовавшись формулой (7), рассчитайте изменение энтропии. Полученные результаты занесите в табл. 2.
Таблица 2
Расчет погрешности
Относительная ошибка: Абсолютная ошибка: Δ(ΔS) = ΔS ε Задачи 1. Найти изменение энтропии 1 кг воды при нагревании ее в чайнике от 200 до кипения (1000С). Ответы: 1) 500 Дж/К; 2) 25,5 Дж/К; 3) 125 Дж/К; 4) 103 Дж/К; 5) 230 Дж/К. 2. Идеальная тепловая машина получает от нагревателя температура которого 500 К за один цикл 3360 Дж теплоты. Найти количество теплоты, отдаваемое за один цикл холодильнику, температура которого 400 К. Ответы: 1) 2688 Дж; 2) 3273 Дж; 3) 685 Дж; 4) 931 Дж; 5) 5850 Дж. 3. Температура холодильника идеального теплового двигателя равна 270С, а температура нагревателя на 900С больше. Каков КПД этого двигателя? Ответы: 1) 30 %; 2) 23 %; 3) 46 %; 4) 77 %; 5) 66 %. 4. Определить изменение энтропии 10 г воды при отвердении ее в лед при 00С. Ответы: 1) –20,8 Дж/К; 2) 17,7 Дж/К; 3) –56,4 Дж/К; 4) –12,3 Дж/К; 5) 31,7 Дж/К. 5. Газ совершающий цикл Карно за счет каждых 2 кДж энергии, полученной от нагревателя, производит работу 600 Дж. Во сколько раз абсолютная температура нагревателя больше абсолютной температуры холодильника? Ответы: 1) 1,3; 2) 1,4; 3) 1,6; 4) 1,5; 5) 1,7. 6. Определить изменение энтропии 20 г олова при изменении температуры от 270С до 2100С. (с=0,23.103 Дж/кг.К) Ответы: 1) 12,8 Дж/К; 2) 2,35 Дж/К; 3) 4,39 Дж/К; 4) 17,8 Дж/К; 5) 2,16 Дж/К.
Контрольные вопросы 1. Второе начало термодинамики. 2. Чему равно КПД тепловой машины, цикла Карно? 3. КПД каких тепловых машин максимально? 4. Свойства энтропии. 5. Формула Больцмана для энтропии. Физический смысл энтропии. 6. Свободная и связанная энергия. 7. Вывод рабочей формулы. 8. Почему процесс плавления идет при постоянной температуре? 9. Объясните график плавления кристаллических тел.
Литература 1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. с. 289–300. 2. Трофимовa Т. И. Курс физики. М.: Высшая школа, 2002, с.111–114. 3. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989, с.129, 133. Лабораторная работа 1.14 Определение коэффициента поверхностного натяжения жидкости Краткая теория
1. Жидкостями называются тела, которые имеют определенный объем, но не имеют своей формы, принимают форму сосуда, в котором они находятся. Они резко отличаются от газа и твердого тела. Газ не имеет ни своего объема, ни своей формы (и то и другое зависит от сосуда, в котором находится газ). Твердое тело имеет свой объем и свою форму. Это различие обусловлено характером теплового движения молекул и силами молекулярного взаимодействия. В жидкостях среднее расстояние между молекулами того же порядка, что и их размеры, поэтому перемещение молекул в объеме крайне затруднено. Движение молекул можно представить так: молекула жидкости в течение некоторого времени колеблется около определенного положения равновесия, затем под воздействием окружающих молекул она скачком меняет место равновесия, перемещаясь на расстояние порядка размера молекулы. Таким образом, молекулы жидкости можно разделить на две группы: одна из них газоподобна и совершает беспорядочные перемещения (кочующие молекулы), другая находится в колебательном движении (оседлые молекулы). Между оседлыми и кочующими молекулами существует динамическое равновесие. С ростом температуры возрастает доля кочующих молекул.
В газах молекулы располагаются совершенно неупорядоченно. В твердом теле частицы тела плотно упакованы и образуют кристаллические решетки, для которых характерна полная упорядоченность (дальний порядок). Жидкости обладают частично упорядоченной структурой (ближний порядок). Число ближайших соседей у фиксированных молекул будет примерно таким же, как и у частиц твердого тела, однако на далеких расстояниях расположение молекул жидкости будет не упорядоченным. Если в твердом теле кристаллическая решетка сохраняется со временем, то в жидкости структура ближнего порядка непрерывно меняется вследствие малости времени оседлой жизни молекул (t» 10–11 с). Жидкости, как и газы, обладают текучестью, любая неуравновешенная сила вызывает их течение. Это свойство коренным образом отличает их от твердых тел, где текучесть может проявиться под воздействием только сил, превосходящих предел упругости. Текучестью жидкости объясняется тот факт, что в широких сосудах, находящихся в поле силы тяжести, ее поверхность горизонтальна. Если жидкость освободить от действия силы тяжести, то она примет форму шара. 2. Внутреннее давление в жидкости. На каждую молекулу со стороны окружающих ее молекул действует сила притяжения на расстоянии R. Проведенную сферу этим радиусом называют сферой молекулярного действия. Каждая молекула взаимодействует только с непосредственно прилегающими к ней молекулами (на рис.1 это выделенные цветом молекулы).
Иначе обстоит дело с молекулой, находящейся на поверхности (рис 2.) жидкости. Так как концентрация молекул в газе намного меньше концентрации молекул в жидкости (расстояние между молекулами в газе намного больше, чем в жидкости и взаимодействием между молекулами в газе можно пренебречь), то результирующая сила Оно оказывается огромным, что объясняет несжимаемость жидкости. Молекулы в жидкости оказываются сжатыми на таком расстоянии, что небольшое уменьшение расстояния между молекулами приводит к резкому возрастанию сил межмолекулярного отталкивания.
Поверхностное натяжение стремится сократить свободную поверхность жидкости, поэтому поверхность подобна растянутой упругой пленке, в которой возникает сила поверхностного натяжения, которая: 1. Направлена по касательной к поверхности. 2. Перпендикулярна произвольной линии, проведенной по поверхности жидкости. 3. Пропорциональна длине линии
где Коэффициент поверхностного натяжения численно равен силе поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность жидкости. Единица измерения [a] = [Н/м]. Коэффициент поверхностного натяжения, а следовательно, и сила поверхностного натяжения, зависят от химического состояния жидкости и от ее температуры. С ростом температуры расстояние между молекулами возрастает, а силы межмолекулярного взаимодействия падают, что приводит к уменьшению силы и коэффициента поверхностного натяжения.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 737; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

 .
.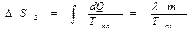 .
. . (7)
. (7)

 Газообразное, жидкое и твердое (кристаллическое) состояния вещества различаются степенью упорядоченности пространственного расположения частиц. Схематическое расположение частиц в газе жидкости и твердом кристаллическом теле показано на рис.1.
Газообразное, жидкое и твердое (кристаллическое) состояния вещества различаются степенью упорядоченности пространственного расположения частиц. Схематическое расположение частиц в газе жидкости и твердом кристаллическом теле показано на рис.1. Рассмотрим молекулы жидкости, которые находятся на поверхности и внутри (рис.2). Молекула, которая находится внутри жидкости, со всех сторон окружена такими же молекулами. В результате результирующая сила притяжения равна нулю
Рассмотрим молекулы жидкости, которые находятся на поверхности и внутри (рис.2). Молекула, которая находится внутри жидкости, со всех сторон окружена такими же молекулами. В результате результирующая сила притяжения равна нулю  .
. и направлена внутрь жидкости перпендикулярно ее поверхности. В результате поверхностный молекулярный слой жидкости будет оказывать на всю жидкость давление, равное сумме результирующих сил поверхностных молекул. Это давление называется внутренним или молекулярным.
и направлена внутрь жидкости перпендикулярно ее поверхности. В результате поверхностный молекулярный слой жидкости будет оказывать на всю жидкость давление, равное сумме результирующих сил поверхностных молекул. Это давление называется внутренним или молекулярным. Силы сцепления между молекулами поверхности приводят к поверхностному натяжению (рис.3).
Силы сцепления между молекулами поверхности приводят к поверхностному натяжению (рис.3). . (1)
. (1)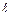 – длина линии на поверхности жидкости, a – коэффициент поверхностного натяжения.
– длина линии на поверхности жидкости, a – коэффициент поверхностного натяжения.


