
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение приращения энтропии при плавлении оловаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Краткая теория Термодинамика – раздел физики, в котором изучается связь между различными макроскопическими величинами и энергетическими характеристиками системы. Особенностью термодинамического подхода является отсутствие представлений о внутреннем строении системы, что делает выводы термодинамики наиболее общими, хотя и более формальными.
Первое начало термодинамики Количество теплоты dQ, сообщаемое системе, расходуется на изменение внутренней энергии системы dU и совершение работы против внешних сил dQ=dU+dA.
Первое начало термодинамики выполняется в любых системах и при любых условиях. Однако первое начало не позволяет указать направление самопроизвольных процессов в природе, на этот вопрос отвечает второе начало термодинамики. Теплота не может сама собой переходить от менее нагретого тела к более нагретому. Однако эта формулировка не запрещает принудительно переходить теплу от менее нагретого к более нагретому. При таком переходе происходят изменения либо в термодинамической системе, либо в окружающей среде. Невозможен такой периодический процесс, единственным результатом которого было бы превращение всей полученной машиной теплоты в работу. Данную формулировку можно упростить. Невозможно создать вечный двигатель второго рода. Вечным двигателем второго рода называется воображаемый двигатель, превращающий в работу всю полученную теплоту. Таким образом, даже в идеальной тепловой машине, не все полученное количество теплоты переходит в работу, часть переходит в окружающее пространство. Работа, которую совершает машина, равна
dA=dQ1–dQ2, где dQ1 – количество теплоты, переданное рабочему телу от нагревателя, dQ2 – количество теплоты, не использованное рабочим телом и переданное холодильнику. КПД такой машины всегда меньше единицы и равен:
Следовательно, для работы тепловой машины необходимо наличие нагревателя с температурой T1 и холодильника с температурой T2. Причем T1> T2. Французский инженер Карно показал, что из всех тепловых машин, работающих при температуре нагревателя T1 и температуре холодильника T2, наибольшим КПД обладает машина, совершающая круговой процесс, называемый циклом Карно (рис 1). КПД такой машины равен:
Таким образом, КПД любой машины не может быть больше КПД машины Карно.
Здесь знак "<" относится к необратимым машинам, а знак "=" к обратимым. Обратимым циклом или процессом называется такой процесс, при котором рабочее вещество (газ) как в прямом так и в обратном процессе переходит через те же самые состояния. По схеме на рис.1 можно догадаться, почему даже идеальная машина не может иметь КПД = 1. При КПД =1 передача теплоты холодильнику отсутствует, т.е. dQ2 =0, но тогда рабочее тело нагреется до температуры нагревателя и прекратится передача тепла рабочему телу, цикл прекратится. Энтропия В механике равновесное состояние системы определялось минимумом энергии, однако в термодинамике этого условия уже недостаточно, например:
Величина
Выражение (5) называется неравенством Клаузиуса. Для простоты рассмотрим обратимый процесс. Из теории криволинейных интегралов известно, что если криволинейный интеграл равен нулю, то под интегралом стоит полный дифференциал некоторой функции S. Т.е. dQ/T=dS. Функция S была названа энтропией. В общем случае
Свойства энтропии 1. Энтропией называется функция dS состояния системы, дифференциал которой в элементарном обратимом процессе равен отношению бесконечно малого количества тепла dQ, сообщенного системе, к абсолютной температуре Т последней. Функцией состояния системы называется функция, которая является полным дифференциалом, и зависит лишь от начального и конечного состояния, а не от формы пути по которому изменялась система.
2. Энтропия в изолированных системах в случае обратимых процессов не изменяется, а в необратимых процессов возрастает. 3. Энтропия – величина аддитивная. Если система состоит из нескольких частей, каждая из которых имеет свою энтропию, то энтропия всей системы равна сумме энтропий отдельных частей. 4. Энтропия является меройбеспорядка системы. 5. Энтропия является мерой «обесценивания» энергии.
Энтропия и вероятность Физический смысл энтропии можно установить из тесной связи с термодинамической вероятностью системы. Выше мы показали, что при самопроизвольных процессах в системе энтропия возрастает, приводя систему в более вероятностное состояние, которое является равновесным. Т.е. возрастание энтропии приводит к росту термодинамической вероятности системы. Больцман установил:
S=k ln W, (6)
где k – постоянная Больцмана, W – термодинамическая вероятность. Уравнение Больцмана – энтропия системы пропорциональна логарифму термодинамической вероятности.
Если книги расположить строго по высоте, то возможность переставить их на полке имеет минимальное число. Т.е. число перестановок книг на полке (число микросостояний), удовлетворяющих условию макросостояния (книги располагаются по высоте), минимально, а порядок максимален. И, наоборот, если книги лежат как угодно, то выполнить это условие возможно бесконечным числом перестановок. Т.е. беспорядок имеет максимальное число микросостояний, и он легко наступает. Этот рисунок показывает, что в природе естественным образом все стремится к беспорядку (он легче наступает), т.е. к максимальному значению энтропии.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.62.85 (0.012 с.) |

 . (1)
. (1) . (2)
. (2) . (3)
. (3)
 . (4)
. (4) , т.е. отношение теплоты, полученной телом, к температуре процесса называется приведенной теплотой. Соотношение (4) показывает, что сумма приведенных теплот в цикле меньше или равна нулю. Так же как и раньше, знак "<" относится к необратимым циклам, а знак "=" к обратимым. Клаузиус показал, что этот результат справедлив для любого цикла и записывается:
, т.е. отношение теплоты, полученной телом, к температуре процесса называется приведенной теплотой. Соотношение (4) показывает, что сумма приведенных теплот в цикле меньше или равна нулю. Так же как и раньше, знак "<" относится к необратимым циклам, а знак "=" к обратимым. Клаузиус показал, что этот результат справедлив для любого цикла и записывается: . (5)
. (5) , где знак ">" относится к необратимым процессам, а знак "=" – к обратимым.
, где знак ">" относится к необратимым процессам, а знак "=" – к обратимым.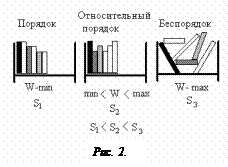 Термодинамической вероятностью называется число микросостояний, соответствующих данному макростоянию системы. В качестве примера рассмотрим книжную полку с книгами (рис.2).
Термодинамической вероятностью называется число микросостояний, соответствующих данному макростоянию системы. В качестве примера рассмотрим книжную полку с книгами (рис.2).


