
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Состояния. Закон возрастания энтропии.Содержание книги
Поиск на нашем сайте
А) Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Обратимым может быть только равновесный процесс.
Обратимый процесс обладает следующими свойствами: если при прямом ходе на каком-то элементарном участке (рис. 9.8.) система получает тепло В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые. Энтропия. Энтропи́я — мера беспорядка системы, состоящей из многих элементов. Рассмотрим обратимый круговой термодинамический процесс, представленный на рис. 3.12. Для этого процесса может быть записано равенство Клаузиуса в виде
где первый интеграл берется по траектории
Изменение направления протекания процесса
Из полученного выражения следует, что для обратимых процессов интеграл С аналогичной ситуацией мы уже встречались, когда в механике рассматривали определение работы консервативной силы. Независимость работы консервативной силы от формы траектории движения тела позволила ввести функцию, названную потенциальной энергией, которая зависит только от состояния механической системы и не зависит от того, как в это состояние система была переведена. Из этой аналогии следует, что элементарное приведенное количество теплоты
Тогда интеграл
Итак, величина Из выражения (3.53) следует, что термодинамическая энтропия, так же как и потенциальная энергия, определяется с точностью до произвольной постоянной. Это связано с тем, что формула (3.53) не позволяет определить абсолютное значение термодинамической энтропии, а дает только разность энтропий для двух равновесных состояний, как суммарную приведенную теплоту в обратимом термодинамическом процессе, переводящим систему из одного состояния в другое. Термодинамическая энтропия, введенная выше, применима для описания равновесного состояния термодинамической системы. Для нахождения энтропии
где: Следовательно, термодинамическая энтропия макроскопической системы, состоящей из находящихся в равновесии подсистем, равна сумме энтропий этих подсистем. Свойство аддитивности энтропии позволяет описывать состояния макроскопической системы, не находящейся в равновесии, путем её разбиения на достаточно большое число подсистем, которые можно считать находящимися в состоянии локального равновесия.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 643; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.105.80 (0.005 с.) |

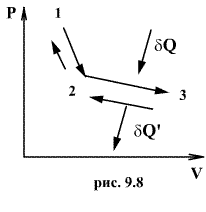
 и совершает работу
и совершает работу  , то при обратном ходе на том же участке система отдает тепло
, то при обратном ходе на том же участке система отдает тепло  и над ней совершается работа
и над ней совершается работа  . По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго.
. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращение системы в первоначальное состояние в окружающих телах не должно оставаться никаких изменений. Например шарик на пружине в вакууме колеблется бесконечно долго. ,
,
 , а второй - соответственно по траектории
, а второй - соответственно по траектории  .
.
 на противоположное
на противоположное  , что можно выполнить вследствие обратимости процесса
, что можно выполнить вследствие обратимости процесса  , приводит к замене знака перед вторым интегралом формулы (3.50). Выполнение этой замены и перенос второго интеграла в выражении (3.50) в правую часть дают
, приводит к замене знака перед вторым интегралом формулы (3.50). Выполнение этой замены и перенос второго интеграла в выражении (3.50) в правую часть дают .
.
 не зависит от конкретного вида траектории, по которой происходит процесс, а определяется только начальным и конечным равновесными состояниями термодинамической системы.
не зависит от конкретного вида траектории, по которой происходит процесс, а определяется только начальным и конечным равновесными состояниями термодинамической системы. должно представлять собой полный дифференциал некоторой функции
должно представлять собой полный дифференциал некоторой функции 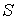 , зависящей только от состояния термодинамической системы, то есть:
, зависящей только от состояния термодинамической системы, то есть: .
где
.
где  — приращение энтропии;
— приращение энтропии;  — минимальная теплота, подведённая к системе; T — абсолютная температура процесса.
— минимальная теплота, подведённая к системе; T — абсолютная температура процесса.
 будет равен разности значений функции
будет равен разности значений функции 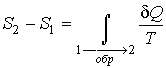 .
.
 ,
,
 - энтропии подсистем,
- энтропии подсистем,  - число подсистем.
- число подсистем.


