
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Е) что такое кпд теплового двигателя. Может ли кпд быть больше или равным единице. Что называют циклом карно. Из каких процессов он состоит. Начертите иСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
А) Теплово́й дви́гатель — устройство, совершающее работу за счет использования внутренней энергии топлива, тепловая машина, превращающая тепло в механическую энергию, использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Работа, совершаемая двигателем, равна:
· · Двигатель Стирлинга (Периодический тепловой двигатель) Дви́гатель Сти́рлинга — тепловая машина, в которой жидкое или газообразное рабочее тело движется в замкнутом объёме, разновидность двигателя внешнего сгорания. Основан на периодическом нагреве и охлаждении рабочего тела с извлечением энергии из возникающего при этом изменения объёма рабочего тела. Может работать не только от сжигания топлива, но и от создания разницы температур его цилиндров. Рабочее тело в теплотехнике и термодинамике условное несменяемое материальное тело, расширяющееся при подводе к нему теплоты и сжимающееся при охлаждении и выполняющее работу по перемещению рабочего органа тепловой машины. В теоретических разработках рабочее тело обычно обладает свойствами идеального газа. Б) Дело в том, что цикл Карно состоит из мало отличающихся между собой изотерм и адиабат. Практическая реализация этого цикла малоперспективна. Цикл Стирлинга позволил получить практически работающий двигатель в приемлемых габаритах.
В) ОБРАТИМЫЙ ПРОЦЕСС в термодинамике процесс, который возможно осуществить в обратном направлении, последовательно повторяя в обратном порядке все промежуточные состояния прямого процесса. Обратимым процессом может быть только равновесный процесс. Реальные процессы, строго говоря, являются необратимыми процессами. Нагреватель — устройство для нагревания (обогрева) чего-либо.(рабочего тела) Для функционирования тепловой машины обязательно необходимы следующие составляющие: нагреватель, холодильник и рабочее тело. При этом, если необходимость в наличии нагревателя и рабочего тела обычно не вызывает сомнений, то холодильник как составная часть тепловой машины в её конструкции зачастую отсутствует. В качестве холодильника выступает окружающая среда.
Г)
Д) формулировка второго начала термодинамики основывается на понятии энтропии:
Е) В соответствии с первым началом термодинамики (1.4), при осуществлении кругового процесса, из-за возвращения рабочего тела в исходное состояние, его внутренняя энергия за цикл не изменяется. Поэтому совершенная рабочим телом механическая работа равна разности подведенной и отведенной теплоты:
Тепловой коэффициент полезного действия (к.п.д.) цикла любой тепловой машины можно рассчитать как отношение полезной работы
Из выражения (3.2) следует, что к.п.д. любой тепловой машины всегда меньше единицы, так как часть полученной от нагревателя теплоты должна передаваться холодильнику. Цикл Карно Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов.
При первом изотермическом процессе 1-2 происходит передача рабочему телу теплоты
Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно
Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику
Отсюда коэффициент полезного действия тепловой машины Карно равен
Полученное выражение позволяет определить коэффициент полезного действия цикла Карно обратимой тепловой машины, если в ней в качестве рабочего тела используется идеальный газ. КПД такой тепловой машины всегда меньше единицы и полностью определяется температурами нагревателя и холодильника.
12.а) Адиабатный процесс. Как осуществляют адиабатный процесс на практике? б) Формулы и график адиабатного процесса в V-p координатах. Сравнение с Изотермическим процессом.
Адиаба́тный проце́сс — термодинамический процесс в макроскопической системе, при котором система не обменивается тепловой энергией с окружающим пространством. Если термодинамический процесс в общем случае являет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии, то адиабатический процесс в силу отсутствия теплообмена (
где
Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением
где
График адиабаты (жирная линия) на С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду
где
Поскольку Вывод уравнения Согласно закону Менделеева — Клапейрона[6] для идеального газа справедливо соотношение
где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными
Если в (3) подставить
или, введя коэффициент
Это уравнение можно переписать в виде
что после интегрирования даёт:
Потенцируя, получаем окончательно:
что и является уравнением адиабатического процесса для идеального газа. При адиабатическом процессе показатель адиабаты равен
Адиабатический процесс может быть реализован в газе либо путём его термоизоляции, либо за счёт быстрого протекания процесса, когда процесс теплопередачи не успевает произойти. Первый способ применялся в опытах Джоуля, где было принципиально необходимо достижение газом состояния, близкого к равновесному. Поэтому каждый из опытов требовал продолжительного времени (около часа) и возникала необходимость введения поправок на тепловые потери.
Примером быстропротекающего процесса является распространение звука в воздухе. Несмотря на то, что такой процесс нельзя считать равновесным, опыт показывает, что для его описания возможно применение уравнения Пуассона, полученного в рамках равновесной термодинамики. Осуществить адиабатный процесс можно, окружив систему теплоизолирующей оболочкой. Пример такой оболочки —термос. Но адиабатным может быть и процесс, протекающий так быстро, что теплообмен с окружающей средой не успевает произойти или настолько мал, что им можно пренебречь.
11 а)Теплоемкость тела. Удельная теплоемкость вещества. Молярная теплоемкость вещества. Единица измерения. б) Теплоемкость газа в изопроцессах; в адиабатическом процессе. в) Зависит ли теплоемкость тел от температуры? Приращение температуры тела прямо пропорционально количеству теплоты, сообщенного ему. Для количественного описания этого соотношения вводится коэффициент пропорциональности
Этот коэффициент позволяет определить количество теплоты Единица измерения теплоёмкости в системе СИ — Дж/К.
В самом общем случае для произвольного тела его теплоемкость может зависеть от параметров состояния этого тела, например, от его температуры или объема. Очевидно, что теплоемкость термодинамической системы изменяется при изменении количества вещества в ней. Для систем, находящихся в состоянии термодинамического равновесия, их теплоемкость пропорциональна количеству вещества. Это позволяет ввести для описания свойств тела удельную теплоемкость:
и, соответственно, молярную теплоемкость:
где:
Теплоемкость, так же как и количество переданной телу теплоты, зависит от того, каким образом, а точнее при осуществлении какого процесса, теплота передавалась этому телу. Если в процессе изменения состояния идеального газа теплоёмкость его не изменяется, то такой процесс называется политропическим. Частными случаями политропического процесса являются рассмотренные ранее изопроцессы, протекающие при постоянных значениях температуры, давления или объема.
Проведем определение теплоёмкости идеального газа в процессе, при котором его объём остаётся неизменным. При таком процессе работа не совершается:
Считая, что внутренняя энергия идеального газа пропорциональна количеству вещества:
его теплоемкость в изохорическом процессе можно определить с помощью формулы:
Здесь:
или, как обычно принято записывать в термодинамике
Символ В соответствии с формулой кинетическая, а, следовательно, и внутренняя энергия идеального газа, линейно зависят от его температуры. Из этого следует, что молярная теплоемкость идеального газа в изохорическом процессе постоянна:
Из этого выражения следует, что внутренняя энергия идеального газа зависит только от его температуры и не зависит от других параметров его состояния, в частности от его объема. Отсутствие зависимости внутренней энергии идеального газа от его объема было экспериментально подтверждёно в опытах Гей-Люссака и Джоуля, схема которых показана на рис. 2.6. Теплоемкость газа в адиабатическом процессе:
В опытах Гей-Люссака адиабатически изолированный жёсткий сосуд имел несколько отделений 1, разделённых перегородками 2, которые можно было медленно извлекать, причём трение в системе практически отсутствовало. В одном из отделений первоначально находился газ, который, по мере открывания перегородок постепенно заполнял другие отделения сосуда, причём каждый раз после открытия перегородки система приходила в состояние термодинамического равновесия. При этом процессе, так как сосуд был адиабатически изолированным, внутренняя энергия газа не изменялась. Опыты показали, что температура газа при этом также не изменяется. Это подтверждало независимость внутренней энергии идеального газа при постоянстве температуры от его объёма. Опыты Джоуля являлись усовершенствованным продолжением опытов Гей-Люссака. Джоуль поместил сосуд в калориметр 3, и тем самым избавил себя от необходимости использовать адиабатически изолированный сосуд. Это дало возможность более тщательно добиваться установления термодинамического равновесия и повысить точность эксперимента. Температуру газа в сосудах Джоуль контролировал посредством измерения температуры воды в калориметре. Опыты Джоуля подтвердили, что внутренняя энергия идеального газа не зависит от занимаемого им объёма. Однако дальнейшие более точные опыты Джоуля, проведённые им совместно с Томсоном (лордом Кельвином) показали, что если газ не является идеальным, его внутренняя энергия зависит от объёма, занимаемого им (эффект Джоуля-Томпсона).
Так как внутренняя энергия идеального газа с точностью до произвольной постоянной равна кинетической энергии теплового движения его молекул, то формула для молярной теплоемкости такого газа:
где число степеней свободы Из формулы (2.65) следует, что для одноатомного газа молярная теплоемкость При использовании выражения Например, для молекул водорода, при температуре порядка 50 К вращательные степени свободы как бы "вымерзают" и его молярная теплоёмкость Теплоемкость идеального газа в процессе, происходящем с изменением объема, отличается от полученного выше выражения Поэтому для произвольного политропического процесса при определении молярной теплоемкости необходимо вместо выражения (2.62) использовать формулу:
где: Если процесс происходит при постоянном давлении, то с учетом выражения
Использование уравнения Клапейрона-Менделеева, записанного для одного моля газа
дает:
Тогда из выражения (2.67) следует формула для нахождения молярной теплоемкости при постоянном давлении:
которая называется соотношением Майера. Из этой формулы с учетом выражения (2.65) имеем:
Анализ выражения (2.70) показывает, что теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме. Это связано с тем, что при изобарическом процессе, в отличие от изохорического, совершается работа, на выполнение которой затрачивается часть подведенной теплоты. Таким образом, молярная теплоёмкость идеального газа зависит от вида процесса, в котором он участвует, и от внешних условий, обеспечивающих протекание этого процесса. Например, в соответствии с определением теплоёмкости П роизведение удельной (на единицу массы вещества) теплоёмкости на атомную массу элемента, из которого состоит твёрдое тело, есть величина почти постоянная. Закон Дюлонга и Пти был установлен ими эмпирически путём проведения большого количества опытов. В этих опытах измерялась скорость охлаждения различных веществ, находящихся при одинаковых внешних условиях, при которых передача теплоты определялась только разностью температуры вещества и окружающей среды. Если для различных веществ разности температур одинаковы, то отношение их теплоёмкостей будет равно обратному отношению скоростей изменения температуры. В то время, когда Дюлонг и Пти проводили свои эксперименты, атомные массы многих элементов ещё не были установлены. Сейчас, с учетом того факта, что молярная масса пропорциональна атомной массе элемента, закон Дюлонга и Пти может быть сформулирован как закон постоянства молярной теплоёмкости (при постоянном объёме) для большинства твёрдых тел, состоящих из простых соединений. Величина этой теплоемкости равна 24,9 Дж/моль*К. Закон постоянства молярной теплоёмкости может быть объяснён равнораспределением энергии по степеням свободы. Считая твёрдое тело состоящим из атомов, каждый из которых представляет собой гармонический осциллятор с тремя степенями свободы, имеем на каждую степень свободы атома среднюю кинетическую энергию
а, соответственно, его молярная теплоемкость примет вид:
что хорошо согласуется с указанным выше значением.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.255.198 (0.012 с.) |

 , где:
, где: — количество теплоты, полученное от нагревателя,
— количество теплоты, полученное от нагревателя,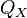 — количество теплоты, отданное охладителю.
— количество теплоты, отданное охладителю.


 .
.
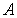 к количеству теплоты
к количеству теплоты  , переданной от нагревателя:
, переданной от нагревателя: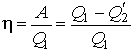 .
.
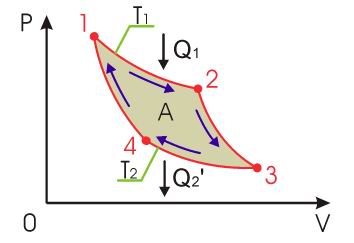
 , причем эта теплота передается бесконечно медленно, при практически нулевой разнице температуры между нагревателем и рабочим телом. Далее рабочее тело подвергается адиабатическому расширению без теплообмена с окружающей средой (процесс 2-3). При последующем изотермическом процессе 3-4 холодильник забирает у рабочего тела теплоту
, причем эта теплота передается бесконечно медленно, при практически нулевой разнице температуры между нагревателем и рабочим телом. Далее рабочее тело подвергается адиабатическому расширению без теплообмена с окружающей средой (процесс 2-3). При последующем изотермическом процессе 3-4 холодильник забирает у рабочего тела теплоту  . Процесс 4-1 представляет собой адиабатическое сжатие, переводящее рабочее тело в первоначальное состояние.
. Процесс 4-1 представляет собой адиабатическое сжатие, переводящее рабочее тело в первоначальное состояние. .
. .
. .
. ) системы со средой сводится только к последним двум процессам[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид
) системы со средой сводится только к последним двум процессам[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид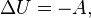
 — изменение внутренней энергии тела,
— изменение внутренней энергии тела, 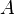 — работа, совершаемая системой.
— работа, совершаемая системой.
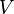 — его объём,
— его объём, 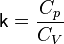 — показатель адиабаты,
— показатель адиабаты, 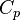 и
и  — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
 диаграмме для газа.
диаграмме для газа. — давление газа;
— давление газа;
 — абсолютная температура газа. Или к виду
— абсолютная температура газа. Или к виду
 всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении
всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении 
 , получаем
, получаем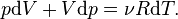
 из (внутр энерг)
из (внутр энерг)  , а затем
, а затем  из
из  , получим
, получим
 :
: .
.
 .
.
 .
. между количеством теплоты, сообщаемого телу, и изменением его температуры, называемым теплоёмкостью:
между количеством теплоты, сообщаемого телу, и изменением его температуры, называемым теплоёмкостью: .
.
 , которое необходимо сообщить телу для повышения его температуры на величину
, которое необходимо сообщить телу для повышения его температуры на величину 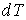 .
.
 ,
,
 - масса тела,
- масса тела, 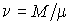 - количество вещества в нем. Эти теплоемкости связаны между собой через молярную массу
- количество вещества в нем. Эти теплоемкости связаны между собой через молярную массу  следующим соотношением:
следующим соотношением: .
.
 , так как нет изменения объема газа.Поэтому, в соответствии с первым началом термодинамики, имеем равенство подведенной к телу теплоты
, так как нет изменения объема газа.Поэтому, в соответствии с первым началом термодинамики, имеем равенство подведенной к телу теплоты  :
: .
.
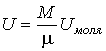 ,
,
 .
.
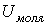 - внутренняя энергия одного моля газа, а молярная теплоемкость при постоянном объем
- внутренняя энергия одного моля газа, а молярная теплоемкость при постоянном объем  равна:
равна: ,
,
 .
.
 после закрывающей скобки указывает на то, что дифференцирование происходит при неизменном значении объема
после закрывающей скобки указывает на то, что дифференцирование происходит при неизменном значении объема  .
. , и не зависит от температуры идеального газа. Тогда выражение для его внутренней энергии с точностью до произвольной постоянной, которую обычно принимают равной нулю, можно записать в следующем виде:
, и не зависит от температуры идеального газа. Тогда выражение для его внутренней энергии с точностью до произвольной постоянной, которую обычно принимают равной нулю, можно записать в следующем виде: .
.
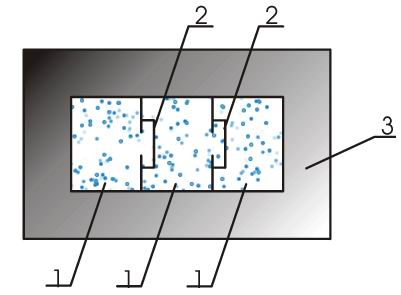
 ,
,
 зависит от физико-химической структуры молекулы газа.
зависит от физико-химической структуры молекулы газа. , а для газа, молекулы которого состоят из двух жестко связанных атомов
, а для газа, молекулы которого состоят из двух жестко связанных атомов  . Соответственно для газов из жестких, многоатомных молекул
. Соответственно для газов из жестких, многоатомных молекул  .
. становится близкой к
становится близкой к  . А при температурах порядка 300 - 400 К вращательные степени свободы "включаются" и его теплоёмкость
. А при температурах порядка 300 - 400 К вращательные степени свободы "включаются" и его теплоёмкость  . При дальнейшем, значительном по сравнению с комнатной, повышении температуры начинают проявляться колебательные степени свободы. Для двухатомного газа, например водорода, это приводит к увеличению энергии его молекулы на величину
. При дальнейшем, значительном по сравнению с комнатной, повышении температуры начинают проявляться колебательные степени свободы. Для двухатомного газа, например водорода, это приводит к увеличению энергии его молекулы на величину  , и соответственно к возрастанию молярной теплоемкости на
, и соответственно к возрастанию молярной теплоемкости на  . Поэтому при очень высоких температурах молярная теплоёмкость водорода стремится к значению
. Поэтому при очень высоких температурах молярная теплоёмкость водорода стремится к значению  .
. ,
,
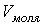 - объем одного моля газа. Последнее слагаемое в числителе этой формулы описывает работу, совершенную одним молем газа в рассматриваемом процессе.
- объем одного моля газа. Последнее слагаемое в числителе этой формулы описывает работу, совершенную одним молем газа в рассматриваемом процессе. .
.
 ,
,
 .
.
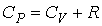 ,
,
 .
.
 , она равна нулю, а для изотермического при
, она равна нулю, а для изотермического при  - бесконечности.
- бесконечности. и такую же среднюю потенциальную энергию. Тогда внутренняя энергия одного моля вещества может быть определена с помощью формулы:
и такую же среднюю потенциальную энергию. Тогда внутренняя энергия одного моля вещества может быть определена с помощью формулы: ,
,
 ,
,



