
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента внутреннего трения жидкостей по методу СтоксаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определение коэффициента трения жидкости. Приборы и принадлежности: цилиндрический сосуд, исследуемая жидкость, шарик, секундомер.
Основные теоретические положения При движении жидкости между ее слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоев. Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения (импульс), вследствие чего последний начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, вследствие чего происходит его торможение. Сила внутреннего трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения и градиенту скорости
где Если принять В системе СИ размерность [h] = кг.м –1.сек –1= 1 Па.с. В СГС [h] = г·см–1·сек–1. В СГС единица коэффициента вязкости называется Пуазом (1 П=10 Па.с). Наряду с коэффициентом динамической вязкости h часто употребляют коэффициент кинематической вязкости rж– плотность жидкости. В СИ [g] = м2.сек., СГС [g] = см2.сек. (1 стокс).
Движение тела в вязкой жидкости На всякое тело, двигающееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от внутреннего трения жидкости, от формы тела, от характера обтекания и т.д. Стоксом было получено строгое решение задачи о ламинарном обтекании шарика безграничной жидкостью. В этом случае сила сопротивления определяется формулой Стокса:
¦ = 6 ph r×v (5) где h–коэффициент внутреннего трения, v –скорость шарика, r –его радиус. Гидродинамический вывод формулы Стокса сложен. Поэтому мы ограничимся анализом задачи с помощью теории размерностей. Прежде чем применять теорию размерностей,нужно на основании физических соображений и опыта установить, от каких параметров может зависеть сила сопротивления жидкости. В нашем случае, очевидно, такими параметрами являются h, v, r и плотность жидкости r ж. Искомый закон следует искать в виде степенного соотношения:
¦=Ava h xry r zж (6)
где A– безразмерный множитель, а a, x и y – подлежащие определению показатели степени. Выбор показателя степени определяется из того требования, что размеренности левой и правой частей должны совпадать. Поскольку размерность выражения определяется степенями при длине, времени и массе,мы получаем три уравнения для нахождения четырех неизвестных a, x, y, z. Легко видеть, что поставленная задача однозначного решения не имеет. Опыт показывает, что при больших скоростях движения (точнее говоря, при больших числах Рейнольдса) сила сопротивления пропорциональна второй, а при малых скоростях (малых числах Рейнольдса) – первой степени скорости. При достаточно медленном движении, таким образом, a=1. Приравнивая показатели степени при массе, длине и скорости в левой и правой частях уравнения, получим:
1=x+z, 1=–x+1+y–3z, –2=–x–1, откуда x=1, y=–1, z=0. Таким образом ¦=Ah r×v Безразмерный множитель А не может быть определен из соображений размерности; строгое решение задачи дает для этого множителя значение 6p.
Метод Стокса
Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют три силы: сила тяжести, выталкивающая (Архимедова) и сила сопротивления, зависящая от скорости. Найдем уравнение движения шарика в жидкости. По второму закону Ньютона
где V – объем шарика,r – его плотность, rж – плотность жидкости, q– ускорение силы тяжести. Интегрируя получим
или после потенцирования
Как видно из полученного выражения скорость шарика вначале увеличивается по экспоненциальному закону до предельного значения Vпред = В вязких жидкостях тела с небольшой плотностью могут достигать критических скоростей очень быстро. Измеряя на опыте установившуюся скорость падения шариков можно определить коэффициент внутреннего трения жидкости по формуле
Эта формула справедлива для шарика, падающего в безгранично простирающейся жидкости. Поэтому в формулу для h вводится поправочный множитель
где R – радиус центра, h – высота жидкости в нем (учитывая влияние стенок и дна цилиндра на падение шарика. Заметим, что коэффициент внутреннего трения жидкости зависит от температуры
где Т – температура жидкости, W – энергия активации, K – постоянная Больцмана. Следовательно, с ростом температуры, особенно в области низких температур, вязкость жидкостей быстро уменьшается в то время, как для газов растет.
Измерения Для измерений используется стеклянный цилиндрический сосуд, наполненный исследуемой жидкостью. На стенках сосуда имеются две метки на некотором расстоянии
Re = Обтекание является ламинарным лишь при не очень больших значениях Rе (£ 10).По результатам опыта следует вычислить число Рейнольдса для использованных размеров шариков, и сделать вывод о максимально допустимом размере шарика для данной установки.
Таблица 1
Примечание. Перед началом измерений записать температуру, при которой проводились опыты.
Расчет погрешности
Ошибку измерений оценим исходя из следующих соображений. В работе коэффициент k=2/9 (ρш – ρж)g считается постоянным и измеряется только отношение r2 / v0 = r2t/S, т.е. η = kr2t/S
Относительная ошибка: Абсолютная ошибка: Δη = η. Ε.
Задачи 1. Какое нужно количество теплоты, чтобы 100 г воды при 100С довести до кипения и 10 г ее испарить? Ответы: 1)45,3.103 Дж; 2) 60,3.103 Дж; 3) 32,3.103 Дж; 4) 18,4.104 Дж; 5) 12,8.104 Дж. 2. К сосуду, в котором находилось 2 л воды при 200С было подведено 1050 кДж теплоты. Определить массу пара, образовавшегося при кипении воды. Ответы: 1) 0,32 кг; 2) 0,12 кг; 3) 0,17 кг; 4) 0,85 кг; 5) 0,55 кг. 3. Какое количество теплоты выделится при конденсации 20 г водяного пара при 1000С и охлаждении полученной воды до 200С? Ответы: 1) 52 кДж; 2) 58 кДж; 3) 123 кДж; 4) 35 кДж; 5)44 кДж. 4. С какой высоты должны упасть дождевые капли, температура которых 200С, чтобы при ударе о Землю они испарились? Сопротивление воздуха не учитывать. Ответы: 1) 29,3.102 м; 2) 51,7.103 м; 3) 26,5.104 м; 4) 21,7.104 м; 5) 18,3.103 м. 5. Имеется 200 г спирта при температуре 200С. Какое количество теплоты нужно израсходовать, чтобы превратить жидкость в пар? Ответы: 1)4,3.102Дж; 2) 2.105Дж; 3) 6,2.104Дж; 4) 4,8.103Дж; 5)5.105Дж. 6. Алюминиевый калориметр массой 50 г содержит 200 г воды при 160С. Какое количество пара нужно ввести в калориметр, чтобы температура в нем повысилась до 900С? Ответы: 1) 22,5 г; 2) 40 г; 3) 35 г; 4) 42,5 г; 5) 62 г.
Контрольные вопросы
1. Что такое вязкость? В каких единицах измеряется коэффициент вязкости, как он зависит от температуры жидкости? 2. Объясните молекулярно-кинетический механизм вязкости. 3. Получите формулу Стокса с помощью теории размерностей. 4. Запишите уравнение движения шарика в жидкости и получите его решение для скорости V(t). 5. Почему, начиная с некоторого момента времени, шарик движется равномерно? 6. Запишите рабочую формулу. 7. Нужно ли вводить поправочный коэффициент (9’) в формулу (9) в ваших измерениях?
Литература
1. Савельев И. В. Курс общей физики, т. 1. М.: Наука, 1989. сс.140–147, 150. 2. Бондарев Б.В., Спирин Г. Г., Калашников Н. П. Курс физики. М.: Курс общей физики, 2003, т.1, с.286–293. Лабораторная работа 1.19
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 910; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.238.150 (0.006 с.) |

 (1)
(1) – градиент скорости в направлении оси x
– градиент скорости в направлении оси x – коэффициент внутреннего трения или динамической вязкости.
– коэффициент внутреннего трения или динамической вязкости.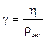 ,
, (7)
(7)
 (8)
(8) . Экспонента очень сильно зависит от своего показателя. Практически после того, как показатель достиг значения –1, она быстро обращается в нуль. Поэтому можно считать, что скорость достигает предельного значения в течение времени t, за которое показатель экспоненты в (8) становится равным –1,т.е. это значение может быть найдено из условия
. Экспонента очень сильно зависит от своего показателя. Практически после того, как показатель достиг значения –1, она быстро обращается в нуль. Поэтому можно считать, что скорость достигает предельного значения в течение времени t, за которое показатель экспоненты в (8) становится равным –1,т.е. это значение может быть найдено из условия  , откуда
, откуда .
. . (9)
. (9) , (9)’
, (9)’ , (10)
, (10)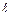 друг от друга. Верхняя метка располагается ниже уровня жидкости с таким расчетом, чтобы скорость шарика к моменту верхней метки успевала установиться. Измеряя расстояние между метками с помощью линейки, а время падения с помощью секундомера, определяют скорость шарика V0 =
друг от друга. Верхняя метка располагается ниже уровня жидкости с таким расчетом, чтобы скорость шарика к моменту верхней метки успевала установиться. Измеряя расстояние между метками с помощью линейки, а время падения с помощью секундомера, определяют скорость шарика V0 =  и по формуле (9) вычисляют h. Результаты экспериментов заносят в табл. 1.При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Характер обтекания определяется значением числа Рейнольдса
и по формуле (9) вычисляют h. Результаты экспериментов заносят в табл. 1.При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Характер обтекания определяется значением числа Рейнольдса (11)
(11)



