
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение средней длины свободного пробега и эффективного диаметра молекул воздухаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Приборы и принадлежности: особая установка, смонтированная на установке, мензурка, секундомер, манометр.
Молекулы газа движутся хаотически, сталкиваются друг с другом и со стенками сосуда.
На длине свободного пробега молекула движется равномерно и прямолинейно. Среднее расстояние, проходимое молекулой между двумя последовательными соударениями, называется средней длиной свободного пробега <l> Оно равно
Чтобы найти среднюю длину свободного пробега, нужно расстояние, пройденное молекулой за единицу времени (т.е. среднюю скорость молекулы < υ >), разделить на число столкновений < Z> за единицу времени:
Поэтому число столкновений в единицу времени определится числом молекул, которые окажутся внутри этого цилиндра. Число столкновений в единицу времени < Z> равно произведению концентрации n на объем цилиндра:
где < υ > – средняя скорость молекулы. По построению она равна длине цилиндра. Если считать, что остальные молекулы тоже двигаются, то в расчеты достаточно добавить поправочный коэффициент
У воздуха при нормальных условиях (t =0 0С или T =273 К, давление Р =105 Па, что соответствует нормальному давлению 760 мм рт. ст.), средняя скорость – 447 м/с, число молекул в единице объема – 1025 в 1 м3, средняя длина свободного пробега – 60 ×10–9 м, число столкновений в 1 секунду 1,8×108 раз, эффективный диаметр молекулы составляет 3×10–10 м. Средняя длина свободного пробега обратно пропорциональна давлению газа (см формулу 3), давление газа пропорционально концентрации n молекул газа (p=nkT), и если <l>, согласно (3), обратно пропорциональна концентрации n, то, следовательно, и обратно пропорциональна p. 2. Рассмотрим теперь понятие эффективного диаметра молекулы.
В газах силы притяжения между молекулами не могут преодолеть силы отталкивания, и молекулы разлетаются во все стороны, занимая весь объем сосуда, в котором находится газ. Газы не имеют определенного объема и формы и легко сжимаются под действием внешнего давления. При столкновениях молекулы приближаются друг к другу на расстояние r =10–10 м между их центрами. На этом расстоянии силы отталкивания резко возрастают за счет перекрытия их электронных оболочек (сила отталкивания носит квантовый характер и поэтому растет значительно быстрее электрической силы притяжения). Действие сил отталкивания приводит к такому же результату, как и столкновение молекул – молекулы отталкиваются друг от друга. Наименьшее расстояние d, на которое приблизятся друг к другу центры молекул при столкновении, называется эффективным диаметром молекул. На расстоянии d вся кинетическая энергия молекул полностью расходуется на совершение работы против сил отталкивания. Расстояние d тем меньше, чем больше кинетическая энергия молекул, т.е. чем выше температура газа. 3. Одним из явлений, позволяющих определить среднюю длину свободного пробега молекул газа, является внутреннее трение в газе. Внутреннее трение возникает между слоями газа (или жидкости), движущимися с разными скоростями. Рассмотрим газ, движущийся в трубке с малым диаметром. Ламинарное движение газа по трубке можно представить в виде слоев, в которых скорости газа постоянны. Вблизи поверхности трубки, вследствие взаимодействия молекул газа с поверхностью, скорость молекул газа вдоль трубки (скорость слоя газа) наименьшая и увеличивается по мере приближения к центру. Распределение скоростей по диаметру трубки можно представить в виде параболы. Вследствие хаотического движения молекула переходит из одного слоя в другой, перенося с собой импульс (количество движения
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 594; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 Расстояние, проходимое молекулой между двумя последовательными соударениями, называется длиной свободного пробега l(рис. 1).
Расстояние, проходимое молекулой между двумя последовательными соударениями, называется длиной свободного пробега l(рис. 1). .
.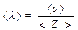 . (1)
. (1) Найдем Z, считая, что все молекулы, кроме одной, покоятся, а единственная молекула движется по оси цилиндра. За единицу времени она столкнется со всеми молекулами, находящимися внутри цилиндра радиусом r, равным эффективному диаметру d эфф молекулы газа и длиной, равной скорости молекулы.
Найдем Z, считая, что все молекулы, кроме одной, покоятся, а единственная молекула движется по оси цилиндра. За единицу времени она столкнется со всеми молекулами, находящимися внутри цилиндра радиусом r, равным эффективному диаметру d эфф молекулы газа и длиной, равной скорости молекулы.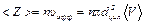 ,
,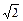 . Тогда окончательно получим:
. Тогда окончательно получим: , (2)
, (2) . (3)
. (3)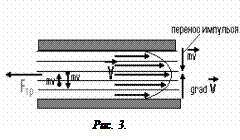 Между молекулами любого вещества одновременно действуют силы взаимного притяжения и отталкивания. Они называются силами молекулярного взаимодействия и имеют электрическое происхождение, поскольку ядра и электроны соседних молекул испытывают электрические силы отталкивания и притяжения. Именно силы межмолекулярного взаимодействия определяют характер теплового движения молекул твердых, жидких и газообразных тел.
Между молекулами любого вещества одновременно действуют силы взаимного притяжения и отталкивания. Они называются силами молекулярного взаимодействия и имеют электрическое происхождение, поскольку ядра и электроны соседних молекул испытывают электрические силы отталкивания и притяжения. Именно силы межмолекулярного взаимодействия определяют характер теплового движения молекул твердых, жидких и газообразных тел. ). В результате, между слоями возникает сила внутреннего трения, направленная противоположно скорости слоев, и стремящаяся выравнить скорости слоев (молекула из быстрого слоя пытается ускорить, а из медленного – замедлить слой, в который она перейдет).
). В результате, между слоями возникает сила внутреннего трения, направленная противоположно скорости слоев, и стремящаяся выравнить скорости слоев (молекула из быстрого слоя пытается ускорить, а из медленного – замедлить слой, в который она перейдет).


