
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение модуля упругости методом изгибаСодержание книги
Поиск на нашем сайте Цель работы: определить модуль упругости стержня методом изгиба. Приборы и принадлежности: две опоры, испытуемые стержни, набор грузов, отсчетный микроскоп.
Краткая теория
Сила характеризует воздействие одного тела на другое. В результате этого воздействия тело может получить ускорение или деформироваться. Деформацией твердого тела называется изменение его размеров и объема. Силы можно разделить на две категории: 1 – силы, обусловленные взаимодействием непосредственно соприкасающихся тел (удар, давление, растяжение, трение и др); 2 – силы, связанные с особой формой материи, называемой полем и осуществляющей взаимодействие между телами без их соприкосновения (силы гравитации, электрические, магнитные, ядерные). При деформации твердого тела, например металла, в нем происходят очень сложные явления, которые еще недостаточно исследованы. Металлы представляют собой совокупность хаотически расположенных и различно ориентированных друг относительно друга мелких кристалликов. Вследствие этого упругие свойства металла по различным направлениям одинаковы и металлы являются изотропными телами. Деформации в металле можно разделить на упругие и пластические. Упругими деформациями называются деформации, при которых после прекращения действия силы, вызывающей деформацию, тело принимает первоначальные размеры и форму. Пластические деформации возникают тогда, когда силы, действующие на тело, перешли определенный предел, называемый пределом упругости и после прекращения действия силы тело не восстанавливает свои размеры и форму. Тело остается деформированным, в нем возникают остаточные деформации. Если после возникновения остаточных деформаций мы продолжаем увеличивать внешнюю силу, то наблюдается разрушение тела. Деформацию металла можно представить так. В зоне упругих деформаций кристаллики металла изменяют свою форму, не сдвигаясь и не разрушаясь. После снятия действия силы они возвращаются в прежнее состояние под действием атомарных сил, действующих между кристалликами. Таким образом, в упругодеформированном теле возникают внутренние силы, которые уравновешивают внешние силы, приложенные к телу. Физическая величина s, численно равная упругой силе dFупр, приходящейся на единицу площади поперечного сечения тела dS, называется механическим напряжением:
Таким образом, напряжение характеризует внутренние силы, возникающие между атомами в кристаллической решетке при деформации тела. Напряжение называется нормальным, если сила dFупр направлена перпендикулярно к площади dS, s0=dF/dS и касательным, если она направлена по касательной к этой площади. Деформации тела бывают разные: растяжение, сжатие, сдвиг, кручение, изгиб. Мерой деформации является относительная деформация
Относительная деформация равна отношению абсолютной деформации D x к первоначальному значению величины x, характеризующей размеры или форму тела.
Английский физик Р. Гук установил законы упругих деформаций. Основной закон (закон Гука): в пределах упругости напряжение, возникающее в теле, пропорционально его относительной деформации.
где К – модуль упругости. Закон Гука справедлив только на участке О–А. При продольном сжатии или растяжении модуль упругости называется модулем Юнга, и закон Гука запишется так:
где E – модуль Юнга. Заменив
Если D Выражение (2) можно преобразовать
где k – коэффициент упругости, а D ℓ или x – удлинение стержня. Выражение (3) также задает закон Гука: при упругих деформациях удлинение стержня пропорционально действующей на стержень силе.
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.009 с.) |

 .
. .
. Зависимость между напряжением s и относительной деформацией e показана на рис. 1, откуда видно, что линейная зависимость s(e) сохраняется лишь в небольшом интервале, до так называемого предела упругости (интервал О–А) s у. Предел упругости – максимальное напряжение, при котором еще возникают упругие деформации. За пределом упругости в теле возникают остаточные деформации (O–F) и график возвращения тела в первоначальное состояние после прекращения действия силы изобразится не кривой О–В, а параллельной ей С–F (параллельно из–за того, что tg угла наклона характеризуется модулем Юнга). В области В–С–D деформация возникает без увеличения напряжения, т.е. тело как бы течет. Это напряжение s т называют пределом текучести. Материалы, для которых область текучести значительна, называют вязкими, а если эта область отсутствует, то – хрупкими. Максимальное напряжение, возникающее в теле до разрушения, называют пределом прочности (sр).
Зависимость между напряжением s и относительной деформацией e показана на рис. 1, откуда видно, что линейная зависимость s(e) сохраняется лишь в небольшом интервале, до так называемого предела упругости (интервал О–А) s у. Предел упругости – максимальное напряжение, при котором еще возникают упругие деформации. За пределом упругости в теле возникают остаточные деформации (O–F) и график возвращения тела в первоначальное состояние после прекращения действия силы изобразится не кривой О–В, а параллельной ей С–F (параллельно из–за того, что tg угла наклона характеризуется модулем Юнга). В области В–С–D деформация возникает без увеличения напряжения, т.е. тело как бы течет. Это напряжение s т называют пределом текучести. Материалы, для которых область текучести значительна, называют вязкими, а если эта область отсутствует, то – хрупкими. Максимальное напряжение, возникающее в теле до разрушения, называют пределом прочности (sр). ,
, , (1)
, (1)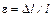 и
и  , получим:
, получим: . (2)
. (2)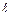 =
=  или F= – kx, (3)
или F= – kx, (3)


