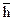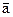Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение коэффициента линейного расширения твердых телСодержание книги
Поиск на нашем сайте Цель работы: теоретически и экспериментально ознакомиться с тепловым расширением твердых тел. Приборы и материалы: оптиметр, термостат, терморегулятор, штангенциркуль, испытуемые образцы.
Краткая теория Опыт показывает, что с повышением температуры происходит расширение твердых тел, называемое тепловым. Для характеристики этого явления вводится коэффициент теплового расширения. Пусть
a – коэффициент линейного расширения. Его физический смысл и единицу измерения определим из выражения:
Коэффициент линейного расширения показывает удлинение единицы длины при нагревании на один градус.
Общая длина тела при температуре t определяется выражением: Коэффициент a в первом приближении зависит от материала и для большинства твердых тел имеет порядок Если тело изотропно, коэффициент объемного расширения av= 3a,
Vt = V0 (1 +av t) В чем причины теплового расширения тел? Большинство тел имеет кристаллическую структуру, рассмотрим эти причины на примере кристаллических тел.
На расстоянии r силы притяжения F пр. и отталкивания F отт. взаимно уравновешиваются. R (r) – равнодействующая этих сил. При увеличении температуры увеличивается амплитуда тепловых колебаний атома решетки. Сделав предположение, что отклонение иона в одну и другую сторону от положения равновесия r одинаковы, т.е., Под действием преобладающей силы отталкивания атом удаляется от соседнего атома на большее расстояние, чем приближается к нему. Таким образом, предположение о равенстве отклонений необходимо заменить неравенством:
А (+) > А (–), где А (–) – максимальное удаление; А (+) – максимальное сближение.
Из графика зависимости потенциальной энергии W от расстояния между частицами тоже можно прийти к выводу о тепловом расширении твердых тел. На рис.2 изображен график зависимости потенциальной энергии от расстояния между атомами в узлах кристаллической решетки. Кривая W несимметрична относительно минимума. По этой причине только малые колебания частиц около положения равновесия будут иметь гармонический характер. С ростом температуры растет кинетическая энергия колебаний частиц, за счет этого увеличивается полная энергия частиц
W 0 = W min, W 1 > W 0, W 2 > W 1. Горизонтальными линиями внутри потенциальной ямы на рис.2 отмечена полная энергия колеблющихся частиц. Полная энергия при данной температуре сохраняется неизменной. При колебаниях кинетическая энергия имеет наибольшее значение в среднем положении. Она становится равной нулю в крайних точках (точки пересечения прямой, соответствующей полной энергии, с графиком потенциальной энергии), так как полностью преобразуется в потенциальную. Частица, как маятник, в крайних положениях меняет направление движения, останавливаясь на мгновение в этих точках. Средние положения частицы В, отмеченные на рис.2 кружочком, с ростом температуры смещаются в сторону больших x, тело расширяется.
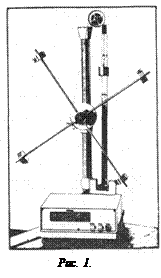
Описание установки Установка для определения коэффициента линейного расширения состоит из термостата и оптиметра.
Горизонтальный оптиметр служит для непосредственного измерения с точностью до 0,001 мм удлинения образца, который находится внутри нагревателя 4 (рис.3). Плоские концы образца должны слегка упираться в наконечники 2. Точная и тщательная установка образца производится после измерения его длины
Порядок работы Предлагается определить a для железа и алюминия. 1. Измерить начальную длину стержня 2. В нагреватель 5 вложить образец; с помощью ручки 7 поднять столик до упора и повернуть его с помощью ручки 3. Затем, действуя в обратном порядке, поместить образец между наконечниками 2. 3. Наблюдая в окуляр 1, совместить нулевое деление шкалы с неподвижным указателем путем вращения ручки 6 – это показание оптиметра при t 1, т.е. при комнатной температуре. 4. Выставить задатчиком на электронном потенциометре заданную температуру t 2, включить установку в сеть. Образец начинает расширяться и шкала двигается. Когда температура образца достигнет заданной, расширение прекратится и шкала остановится. Наблюдают в окуляр, какое деление шкалы стоит против неподвижного указателя – это будет показание оптиметра при t 2. Все данные заносят в таблицу и по формуле вычисляют a:
где
5. Второй опыт проводят аналогично первому, т.е. совмещают нулевое деление шкалы с указателем при температуре t 2, выставляют на потенциометре другую заданную температуру t3, ждут когда шкала перестанет двигаться и снимают показание оптиметра при t3. Данные заносят в таблицу, вычисляют второе значение a по формуле (1), где
D t = t 3 – t 2,
6. Вычислить значение a по результатам обоих опытов. 7. Повторить опыты для другого образца. Для установки начального положения используют микрометрический винт 6. Образец укрепляется между наконечниками так, чтобы в трубку оптиметра 1 был виден правый край шкалы с делениями (стрелку оптиметра в начальный момент устанавливают винтом 6 в положение –80 или –90 мкм).
Расчет погрешности
Относительная ошибка: Абсолютная ошибка: Задачи 1. На сколько удлинится медный телеграфный провод на участке длиной 60 м при повышении температуры от 10 до 40оС? Ответы: 1) 25,3 мм; 2) 41,7 мм; 3) 34,7 мм; 4) 20 мм; 5) 31мм.
2. Железная линейка при 150С имеет длину 1 м. На сколько изменится длина линейки при охлаждении до –350С? Ответы: 1) 6.10–4 м; 2) 6.10–3 м; 3) 4,3.10–4 м; 4) 3,3.10–2 м; 5) 7,2.10–3 м.
3. При температуре 00С вода и керосин занимают одинаковые объемы по 4 л. Найти разность их объемов при 500С. Ответы: 1) 9.10–5 м3; 2) 1,64.10–5 м3; 3) 4,3.10–4 м3; 4) 7.10–4 м3; 5) 3,22.10–4 м3.
4. Как велик должен быть зазор между рельсами зимой при температуре –400С чтобы летом при температуре +400С этот зазор не делался меньше 1 мм? Длина стального рельса при температуре –400с равна 12,5 м. Ответы: 1) 5 мм; 2) 32,0 мм; 3) 13 мм; 4) 18 мм; 5) 23мм.
5. На деревянное колесо, имеющее диаметр 100 см, требуется надеть железную шину, диаметр которой на 5 мм меньше диаметра колеса. На сколько следует для этого повысить температуру шины? Коэффициент линейного расширения железа Ответы: 1) 4170С; 2) 3800С; 3) 5300С; 4) 950С; 5) 5380С.
6. При 00С железная и медная проволоки имеют одинаковую длину, равную 500 м. Определить разность их длин при 300С. Ответы: 1) 10–1м; 2) 8,5.10–2м; 3) 7,5.10–2м; 4) 2,52.10–2м; 5) 8,35.10–2м.
Контрольные вопросы 1. Объясните причины теплового расширения тел. 2. Коэффициент теплового расширения и его физический смысл. 3. Изобразите и объясните график зависимости потенциальной энергии от расстояния между атомами. 4. Расскажите об экспериментальной установке и ходе выполнения работы. 5. Сравните полученные данные с табличными.
Литература
1. Савельев И. В. Курс общей физики, т. 2. М.: Наука, 1989. 2. Трофимов Т. И. Курс физики. М.: Высшая школа, 2002. 3. Детлаф А. А., Яворский Б. М. Курс физики, М.: Высшая школа, 1989. Лабораторная работа 1.16 Маятник Обербека
Цель работы: изучение динамики вращательного движения, оценка влияния трения на точность результатов проведенных измерений.
Оборудование: лабораторная установка.
Материал для изучения: уравнения динамики вращательного движения, момент инерции, сила трения, оценка погрешностей измерений.
Теоретическое введение
I ω = Мвнеш, (1)
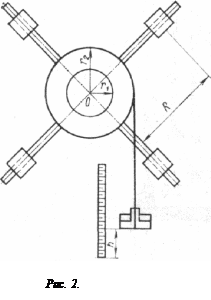
где I — момент инерции тела; ω — угловое ускорение Мвнеш – сумма проекций на ось вращения моментов внешних сил. На рис. 2 схематически показан прибор, с помощью которого удобно исследовать уравнение (1). Он называется маятником Обербека. Четыре спицы укреплены на втулке под прямым углом. На спицах находятся грузы массой mгр каждый. Втулка и два шкива радиусами r1 и r2 насажены на общую ось. Ось закреплена в подшипниках так, что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции I тела. На шкив намотана нить, к которой привязана платформа известной массы. На платформу кладется груз, нить натягивается и создает вращающий момент
M=Tri, (2)
где Т – сила натяжения нити, r1 — радиус шкива (гi равен r1 или r2). Силу Т можно найти из уравнения движения платформы с грузом:
mg–T=ma, (3)
где m — масса платформы с грузом, а — ее ускорение. Ускорение а связано с угловым ускорением ε =
ε =а/r. (4)
Из уравнений (2) и (3) получаем, что момент силы натяжения нити
М = Тг=m(g — а)r. (5)
Кроме того, на маятник действует момент силы трения в оси Mтр. С учетом этого уравнение (1) имеет вид:
m(g–a)r–Mтр=Ia/r. (6)
В уравнение (6) входит ускорение (а) платформы. Это ускорение можно довольно просто определить. Действительно, измеряя время t, в течение которого платформа с грузом опускается на расстояние h, можно найти ускорение а:
a=2h/t2. (7)
Тогда
Формула (8) дает связь между ускорением а, которое можно измерить опытным путем, и моментом инерции I. В формулу (8) входит неизвестная величина — момент силы трения Mтр. Хотя интуитивно понятно, что момент силы трения мал, тем не менее он не настолько мал, чтобы им в (8) можно было полностью пренебречь. Если положить Mтр = 0, то можно убедиться, что результаты опыта будут отличаться от зависимости (8). Можно по порядку величины экспериментально определить Мтр и это нужно, конечно, сделать в начале работы. Для этого, с помощью нескольких грузов увеличивая силы натяжения Т нити, найдите минимальное значение массы m0, при которой маятник начнет вращаться. Дальнейшие измерения нужно проводить с грузами массой m ≥10 m0. На первый взгляд относительную роль момента силы трения можно уменьшить, если взять грузы массой m >> m0, допустим, груз m = 103 m0. Однако это не так по двум причинам. Первая — увеличение массы груза приводит к увеличению силы давления N на ось, а значит и к росту момента силы трения Мтр = μ Nr, где μ — коэффициент трения, r – плечо силы трения. Вторая причина состоит в том, что увеличение m уменьшает время падения t, а значит, ухудшает точность измерения ускорения а [см. (8)]. Момент инерции, входящий в (8), согласно теореме Гюйгенса— Штейнера может быть записан в виде:
I = I0 + 4mгрR2. (9)
Здесь R – расстояние центров грузов mгр от оси вращения, I0=I (R =0), т.е. равен моменту инерции системы при R = 0. В (8) входит также отношение:
В условиях опыта оно меньше или порядка 10–2 (убедитесь в этом!). Пренебрегая этой величиной в знаменателе выражения (8). получаем формулу, которую можно проверить экспериментально:
Измерения Представляет интерес экспериментально исследовать две зависимости. Первая — зависимость углового ускорения ε от момента внешней силы М = mgr при условии, что момент инерции I остается постоянным. Если на оси ординат откладывать угловое ускорение е, а на оси абсцисс — mgr, то, согласно (10), экспериментальные точки должны ложиться на прямую. Из (10) видно, что наклон этой прямой равен 1/I, а точка пересечения с осью абсцисс дает Мтр. Если экспериментальные данные подтверждают линейную зависимость ε от mgr, то можно приступить к изучению второй зависимости — зависимости момента инерции I от расстояния R грузов mгр до оси вращения маятника (рис. 1). Согласно теореме Гюйгенса—Штейнера: I(R) =Iо + 4mгрR2. Выясним, как проверить эту зависимость экспериментально. Для этого преобразуем соотношение (10), пренебрегая в нем малой величиной (моментом силы трения Мтр) по сравнению с моментом mgr. Из (10) имеем:
Следовательно
Из (11) понятно, как экспериментально проверить зависимость (11): нужно, выбрав постоянную массу m груза, измерять ускорение а при различных положениях R грузов mгр на спицах. Результаты измерений удобно изобразить в виде точек на координатной плоскости ХОУ, где х = (R/r) 2, у = g/а. Если экспериментальные точки в пределах точности измерений ложатся на прямую, то это подтверждает зависимость (11), а значит, и формулу
I(R)=I0+4mгрR2.
Отметим, что при выводе формулы (11) мы пренебрегли моментом сил трения, т.е. считали, что Мтр << mgr. Значение Мтр получено из графика зависимости ε = ε (mgr) при R = const. Это и позволяет выбрать массу перегрузки так, чтобы неравенство mgr >> Мтр заведомо выполнялось. Роль момента сил трения можно оценить и иначе. Для этого заметим, что если маятник в начальный момент вращается с угловой скоростью ω0, то к моменту остановки он повернется на угол φ, определяемый из соотношения
где Атр — работа сил трения. В (12) предполагается, что момент сил трения является постоянной величиной и связан с угловым ускорением соотношением
I ε 0=Mтр, (13)
где ε 0 — ускорение, определяемое только моментом сил трения. Из (12) и (13) находим
Пусть n – полное число оборотов, которое делает маятник до остановки, а Т0 – период вращения маятника в начале движения. Тогда
и из (14) получаем:
Отсюда ясно, как на опыте определить ε0: нужно измерить время Т0 за которое совершается первый оборот и полное число n оборотов маятника до остановки. Во всех дальнейших измерениях нужно следить, чтобы выполнялось неравенство ε0<< ε.
Задание 1. Сбалансируйте маятник. Для этого оставьте на крестовине два груза на двух противоположных спицах на равных расстояниях от оси вращения. Спицы, на которых находятся грузы, соединены со втулкой резьбой. Вращая спицы в резьбе, добейтесь равновесия. Затем точно сбалансируйте грузы на второй паре спиц на таком же расстоянии от оси вращения. Полезно несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. Подумайте, как на основании этих опытов определить, хорошо ли сбалансирован маятник. 2. Определите приближенно минимальную массу m0, при которой маятник начинает вращаться, и оцените момент сил трения из соотношения Mтр≈m0gr, где r — радиус шкива, на котором подвешен груз m0. 3. Оцените ускорение ε0, возникающее под действием момента сил трения. Для этого приведите маятник во вращение, измерьте время T 0, за которое он совершает первый оборот, и полное число оборотов маятника до полной остановки. Затем по формуле (15) вычислите ε0. Измерения повторите три раза и сравните соответствующие им значения ε0. 4. Определите экспериментально зависимость углового ускорения ε маятника от момента приложенной силы mgr. В этой серии измерений момент инерции маятника должен оставаться постоянным: I = const. Для определения зависимости ε = ε (mgr) измерьте время t, за которое груз m опускается на расстояние h. Измерение времени t для каждого груза при постоянном значении h повторите три раза. Затем найдите среднее значение времени падения груза по формуле
и определите среднее ускорение груза из соотношения (7):
Эти измерения и вычисления повторите для пяти значений массы m груза, причем для всех m должно выполняться неравенство m >> m0, где m0 — масса-перегрузка страгивающего маятник (см. п. 2). Результаты измерений запишите в табл. 1.
Таблица 1
r =
1. Время Δ t определяется из соотношения:
2. Угловое ускорение находится по формуле ε = а/r. 3. Δm определяется с точностью, с которой известна масса грузов m. Полученные экспериментально точки отложите в координатной плоскости х=mgr, у =ε и по ним постройте график зависимости
5. Проверьте экспериментально зависимость (11). Для этого, взяв постоянную массу груза m >> m0, определите ускорение а груза m при пяти различных положениях R на спицах грузов mгр. В каждом положении R измерения времени падения t груза m с высоты h повторите три раза. Результаты измерений занесите в табл. 2, где Полученные экспериментальные точки нанесите с учетом погрешностей в координатной плоскости х =(R/r)2, у = g/ Таблица 2
Задачи
1. Определить момент инерции сплошного шара массой m=10 кг и радиусом R=0,1 м относительно оси, проходящей через центр тяжести. Ответы: 1) 0,25.10–2 кг.м2; 2)1,32.10–2 кг.м2; 3) 2,02.10–2 кг.м2; 4) 0,04 кг.м2; 5 5) 0,0431 кг.м2. 2. Цилиндр диаметром 12 см, имеющий массу 3 кг лежит боковой поверхностью на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта с плоскостью. Ответы: 1) 0,0162 кг.м2; 2) 0,0153 кг.м2; 3) 0,0218 кг.м2; 4) 0,0123 кг.м2; 5) 0, 00923 кг.м2. 3. Определить момент инерции тонкого обода радиусом r=0,5м и массой 3 кг относительно оси, проходящей через центр тяжести. Ответы: 1) 0.235 кг.м2; 2) 1,25.10–2 кг.м2; 3) 0,375 кг.м2; 4) 0,575 кг.м2; 5) 0,75 кг.м2; 6) 2,65.10–2 кг.м2. 4. Диск радиусом 0,5 м и массой 20 кг вращается вокруг оси перпендикулярной плоскости диска и проходящей через его центр тяжести. Найти момент инерции диска относительно этой оси. Ответы: 1) 0,250 кг.м2; 2) 2,50 кг.м2; 3) 0,125 кг.м2; 4) 0,0135 кг.м2; 5) 5,5 кг.м2. 5. Определить момент инерции вала массой 5 кг и радиусом R=0,02 м относительно оси, параллельной его оси симметрии и удаленной от нее на расстоянии а=10 см. Ответы: 1) 0,135 кг.м2; 2) 0,0310 кг.м2; 3) 0,0235 кг.м2; 4) 0,0510 кг.м2; 5) 0,205 кг.м2. 6. Маховик вращается по закону, выраженному уравнением φ=А+Вt+Ct2, где А=2 рад, В=–16 рад/с, С=–2 рад/с2. Момент инерции колеса равен 50 кг.м2. Чему равен вращающий момент М? Ответы: 1) –25 Нм; 2) 125 Нм; 3) 75 Нм; 4) –100 Нм; 5) 230 Нм.
Контрольные вопросы
1. Запишите основное уравнение динамики вращательного движения. 2. Устройство и принцип действия маятника Обербека. 3. Как используется теорема Гюйгенса–Штейнера в работе?
Литература 1. Сивухин Д. В. Общий курс физики. Т. 1. Механика. М., 1989. 2. Савельев И. В. Курс физики, т. 1. М., 1989. 3. Детлаф А. А., Яворский Б. М. Курс физики. М., 1989. 4. Каленков С. Г., Соломахо Г. И. Практикум по физике. М.: Высшая школа, 1990. Лабораторная работа 1.17
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |

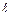 – длина тела при температуре t, удлинение этого тела D
– длина тела при температуре t, удлинение этого тела D 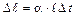 ,
,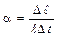 .
.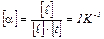 .
.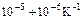 . В действительности он несколько зависит от температуры.
. В действительности он несколько зависит от температуры.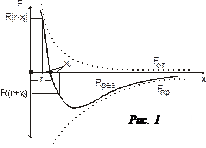 В узлах кристаллической решетки металлического кристалла находятся положительные ионы металла. Между ними беспорядочно, подобно молекулам газа, двигаются электроны. На рис.1 приведены графики сил взаимодействия между частицами в твердых телах.
В узлах кристаллической решетки металлического кристалла находятся положительные ионы металла. Между ними беспорядочно, подобно молекулам газа, двигаются электроны. На рис.1 приведены графики сил взаимодействия между частицами в твердых телах.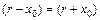 ,получим из графика (рис.1): R (r – x 0) ¹ R (r + x 0). Силы отталкивания между частицами меняются с расстоянием быстрее, чем силы притяжения: R (r – x 0)> R (r + x 0).
,получим из графика (рис.1): R (r – x 0) ¹ R (r + x 0). Силы отталкивания между частицами меняются с расстоянием быстрее, чем силы притяжения: R (r – x 0)> R (r + x 0).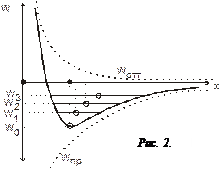 Колебания ионов в узлах происходят ангармонично (т.е. не по гармоничному закону), и расстояние между атомами с ростом температуры растет. Тело расширяется.
Колебания ионов в узлах происходят ангармонично (т.е. не по гармоничному закону), и расстояние между атомами с ростом температуры растет. Тело расширяется.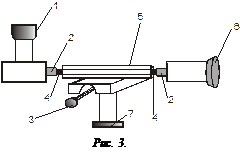 С помощью термостата достигаются заданные температурные условия для испытуемого образца. Инструкция к пользованию установкой для контроля, поддержания и регулирования температуры укреплена на приборе. Температура образца поддерживается постоянной следующим образом. С помощью термопары и электронного потенциометра производится изменение температуры. При достижении заданной температуры, установленной задатчиком, нагреватель отключается, при понижении температуры ниже заданной, нагреватель включается. Таким образом температура образца поддерживается постоянной.
С помощью термостата достигаются заданные температурные условия для испытуемого образца. Инструкция к пользованию установкой для контроля, поддержания и регулирования температуры укреплена на приборе. Температура образца поддерживается постоянной следующим образом. С помощью термопары и электронного потенциометра производится изменение температуры. При достижении заданной температуры, установленной задатчиком, нагреватель отключается, при понижении температуры ниже заданной, нагреватель включается. Таким образом температура образца поддерживается постоянной.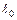 штангенциркулем, занести в таблицу.
штангенциркулем, занести в таблицу.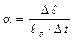 ,
,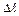 – есть разность показаний оптиметра при t 2 и t 1;
– есть разность показаний оптиметра при t 2 и t 1;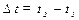 ,
,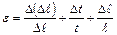
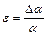 ; Δα = α. ε
; Δα = α. ε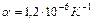 .
.
 В работе изучается динамика вращательного движения. В частности, экспериментально проверяется уравнение моментов для вращения вокруг неподвижной оси
В работе изучается динамика вращательного движения. В частности, экспериментально проверяется уравнение моментов для вращения вокруг неподвижной оси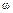 соотношением
соотношением (8)
(8)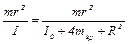 .
.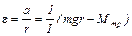 (10)
(10)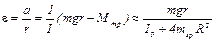 .
.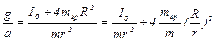 (11)
(11)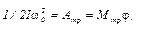 (12)
(12)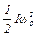 – начальная кинетическая энергия вращающегося маятника,
– начальная кинетическая энергия вращающегося маятника,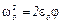 . (14)
. (14)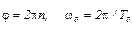 .
.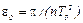 . (15)
. (15)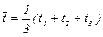
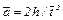 .
.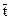
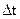
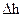
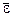

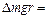

 (рис. 3, а).
(рис. 3, а). определяются так же, как в табл. 1.
определяются так же, как в табл. 1.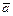 и постройте график зависимости у = у (х) (рис. 3, б).
и постройте график зависимости у = у (х) (рис. 3, б).