
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения удельных теплоемкостей воздухаСодержание книги
Поиск на нашем сайте
Приборы и принадлежности: стеклянный баллон, насос, секундомер, манометр.
Краткая теория
Законы идеальных газов При изучении процессов в газах вводят понятие идеального газа. Газ считается идеальным, если выполняются следующие условия: 1. Размеры молекул газа пренебрежимо малы. 2. Между молекулами отсутствуют силы взаимодействия, 3. Соударения молекул являются упругими. Состояние идеального газа характеризуется тремя термодинамическими параметрами: давлением Р, объемом V, температурой Т. Переход газа из одного состояния в другое, сопровождающийся изменением его параметров, называется процессом. Если один из параметров остается постоянным, то процесс называется изопроцессом. Рассмотрим некоторые изопроцессы.
Изотермический процесс Изотермическим процессом называется процесс, происходящий при постоянной температуре, Т =const. Два других параметра изменяются. Изотермический процесс описывается уравнением:
PV = const – закон Бойля–Мариотта, (1)
который читается: д ля данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная. Изохорический процесс Изохорический процесс происходит при постоянном объеме. Зависимость давления от температуры описывается уравнением:
который читается: для данной массы газа при постоянном объеме давление газа линейно возрастает с увеличением температуры. Изобарический процесс Изобарический процесс. Это процесс, происходящий при постоянном давлении, Р =const. Зависимость объема от температуры описывается законом:
который читается: для данной массы газа при постоянном давлении объем газа линейно возрастает с ростом температуры. Адиабатический процесс Адиабатическим процессом называется процесс, происходящий без теплообмена с окружающей средой (dQ = 0). Он описывается уравнением Пуассона:
pV g=const, (4)
где g –постоянная адиабатического процесса. Постоянная адиабатического процесса равна:
При адиабатическом процессе изменяются все параметры газа: давление, объем и температура. Теплоемкость газа Количество теплоты dQ, сообщенное телу при нагревании, равно
где с – удельная теплоемкость вещества, равная количеству теплоты, сообщаемой единице массы вещества для нагревания ее на один градус. Помимо удельной теплоемкости вводится понятие мольной теплоемкости. Мольная теплоемкость С – равная количеству теплоты, сообщаемой одному молю вещества для нагревания его на один градус. Мольная и удельная теплоемкости связаны между собой соотношением:
С = m×с, (6) где С – мольная теплоемкость, m – молярная масса. Газ можно нагревать при постоянном давлении и при постоянном объеме, поэтому для газа вводятся две теплоемкости: изобарическая и изохорическая. Мольная изобарическая и мольная изохорическая теплоемкости газа связаны с соответственными соотношениями:
Отсюда видно, что отношение мольных теплоемкостей газа равно отношению удельных Количество теплоты, сообщенное 1 молю газа при изохорическом процессе, равно:
а при изобарическом процессе
Первое начало термодинамики Количество теплоты dQ, сообщенное термодинамической системе, расходуется на увеличение ее внутренней энергии dU и на работу dA системы против внешних сил.
dQ = dU + dA. (9)
Внутренняя энергия U – суммарная энергия всех молекул в газе для идеального газа – кинетическая энергия вращательного и поступательного движения. Для одного моля газа определяется выражением
Работа, совершаемая газом, равна
dA = pdV. (11)
где dV – изменение его объема.
Применение первого начало термодинамики Изотермический процесс При этом процессе температура остается постоянной (Т =const) В этом случае dT =0 и внутренняя энергия не изменяются dU =0 dQ=dA, т.е. вся подводимая теплота расходуется газом на совершение работы против внешних сил.
Изохорический процесс При изохорическом процессе V =const, dV =0 и dA =0. Т.е. при этом процессе работа не совершается, т.к. объем не изменяется. Тогда 1 началозапишется: dQ = dU. Т.е. количество теплоты расходуется на изменение внутренней энергии. Но по определению Из этой формулы видно, что изменение внутренней энергии газа определяется только изменением его температуры. Теплоемкость при постоянном объеме (изохорная теплоемкость) равна:
Изобарический процесс В этом процессе изменяются и внутренняя энергия, и работа против внешних сил:
dQ=dU+dA,
т.е. теплота, подводимая к системе, идет на увеличение внутренней энергии и на совершение работы против внешних сил. Для 1 моля газа уравнение Менделеева–Клапейрона
pV=RT; pdV=RdT,
но pdV=dA, поэтому dA=RdT, тогда (Напомним, что Сu и Cp – мольные теплоемкости)
Cp=Cv+R, (13)
R – универсальная газовая постоянная, равная работе расширения одного моля газа при нагревании на один градус в изобарическом процессе. Уравнение (13) называется уравнением Роберта Майера. Из него следует: при изобарном нагревании 1 моля газа на 10 часть теплоты, равная CV, идет на увеличение внутренней энергии, а другая часть, равная R, – на совершение работы против внешних сил.
Адиабатический процесс Так как при адиабатическом процессе dQ =0, то dA=–dU. Первое начало термодинамики будет иметь вид
dU+dA =0 или СVdT+PdV =0.
Откуда следует, что при адиабатическом процессе работа совершается за счет изменения внутренней энергии. Например, если открыть ниппель у автомобильного колеса, то выходящий воздух можно рассматривать как адиабатическое расширение. Работа по расширению воздуха происходит за счет уменьшения внутренней энергии, что приведет к охлаждению воздуха и ниппель станет холодным.
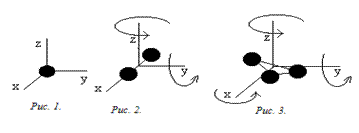
Степени свободы Согласно молекулярно–кинетической теории внутренняя энергия, которая обусловлена движением молекул как поступательным, так и вращательным, определяется (10), где i – число степеней свободы. Числом степеней свободы i называется число независимых координат, полностью определяющих положение молекулы в пространстве. В случае жесткой связи например: 1. У одноатомной молекулы только три степени свободы поступательного движения, i =3 (для атома как материальной точки не учитывается вращательное движение); (рис.1). 2. У двухатомной молекулы три степени свободы поступательного движения и две степени свободы вращательного движения, i =5 (рис.2); 3. У трехатомной молекулы три степени свободы поступательного движения и три степени свободы вращательного движения; i =6 (рис. 3).
Из (10), (11) и (12) можно вычислить внутреннюю энергию и теплоемкости газа, а по формуле (1) определить адиабатическую постоянную g. 1. Для одноатомного газа i =3
Адиабатическая постоянная 2. Для двухатомного газа i =5 и аналогично предыдущему получим
3. Для трехатомного газа i =6
В общем случае:
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 887; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.009 с.) |

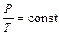 – закон Шарля, (2)
– закон Шарля, (2)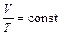 – закон Гей–Люсака, (3)
– закон Гей–Люсака, (3)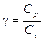 . (5)
. (5)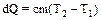 ,
,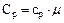 ;
;  .
.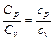 .
. , (7)
, (7) . (8)
. (8) . (10)
. (10) (для 1 моля). Следовательно,
(для 1 моля). Следовательно, 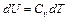 .
. (12)
(12)
 ;
;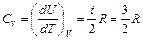 ;
;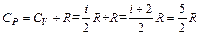 .
.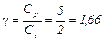 .
.
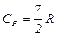
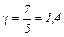
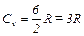 ;
; 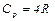

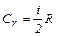 ;
; 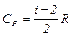 ;
;  .
.


