
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механические колебания и волны.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
192. Физический маятник представляет собой тонкий однородный стержень длиной l =35 см. Определить, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальной. 193. Период колебаний крутильного маятника Т1=4 с. Если на расстоянии R=0.5 м от оси колебаний к нему прикрепить шар массой m=0.3 кг, причем радиус шара много меньше расстояния R, то период колебаний станет равным Т2=8 с. Определить момент инерции маятника. 194. Груз массой m подвешен к системе двух параллельно соединенных пружин жесткостями K 1 и K2. Система выведена из состояния равновесия и предоставлена сама себе. Энергия, сообщенная системе, равна W. Написать уравнение колебаний, определить амплитуду и частоту колебаний. Сопротивлением среды пренебречь. 195. Определить отношение кинетической энергии гармонически колеблющейся точки к ее потенциальной энергии, если известна фаза колебания. 196. Точка одновременно участвует в n гармонических колебаниях одинаковой частоты, направленных вдоль одной прямой: А1sin(wt+j1), А2sin(wt+j2),... Аnsin(wt+jn). Определить амплитуду и фазу результирующего колебания. 197. Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях: x=2cos(πt/2) и y= - cos(πt) (смещение из положения равновесия - в м, время – в секундах). Определить уравнение траектории точки. 198. Амплитуда затухающих колебаний математического маятника за 1 минуту уменьшилась вдвое. Во сколько раз она уменьшится за 3 минуты? 199. Частота колебаний стального шарика радиусом R=0.01 м, прикрепленного к пружине, в воздухе ω0=5.0 с-1, а в жидкости ω=4.06 с-1. Определить вязкость жидкости. 200. Под действием силы F=Аcos(ωt) (A =2 Н, ω=π/3 рад/с) движется тело массой 100 г. Начальная скорость тела равна нулю. Найти зависимость кинетической энергии тела от времени и определить ее максимум. 201. Источник незатухающих гармонических колебаний движется по закону S0=A×sin(ωt). Определить смещение от положения равновесия, скорость и ускорение точки через t=1 с, находящейся на расстоянии l =340 м от источника, если скорость распространения плоских волн равна 340 м/с, А =5 мкм, ω =3140 рад/с. 202. Вагон массой 80 т имеет 4 рессоры. Жесткость пружин каждой рессоры 500 кН/м. При какой скорости вагон начнет сильно раскачиваться вследствие толчков на стыках рельс, если длина рельса 12.8 м? 203. Написать уравнение результирующего колебания, получающегося в результате сложения двух взаимно-перпендикулярных колебаний с одинаковой частотой 0.5 Гц и с одинаковой начальной фазой 600. Амплитуда одного колебания равна 10 см, другого 5 см. 204. Груз массой 500 г, подвешенный на пружине, коэффициент жесткости которой 50 Н/м, помещен в масло. Коэффициент сопротивления в масле r= 0.5 кг/с. На верхний конец пружины действует вынуждающая сила, изменяющаяся по закону F=sin(w t) (сила– в ньютонах, время – в секундах). При какой частоте вынуждающей силы амплитуда вынужденных колебаний будет максимальна? Чему равна максимальная амплитуда? Какова будет амплитуда вынужденных колебаний, если частота вынуждающей силы вдвое меньше резонансной? 205. Математический маятник длиной 24.7 см совершает затухающие колебания. Через сколько времени энергия колебаний маятника уменьшится в 9.4 раза? Логарифмический декремент затухания равен 1. 206. На вертикально отклоняющие пластины осциллографа поданы напряжения U1=5sin(ωt+π/3), U2=10sin(ωt+π/6) и U3=15sin(ωt+π/9) (напряжение – в вольтах, время – в секундах). Определить амплитудное значение напряжения для результирующего колебания. 207. Звуковые колебания с частотой 500 Гц и амплитудой 0.25 мм распространяются в воздухе. Длина волны 70 см. Найти скорость распространения колебаний и максимальную скорость частиц воздуха. 208. Точка участвует одновременно в двух взаимно-перпендикулярных колебаниях x=cos(pt) и y=cos(0.5pt) (смещение из положения равновесия - в метрах, время – в секундах). Найти траекторию движения точки. 209. Точка участвует одновременно в двух взаимно-перпендикулярных колебаниях x=2cos(wt) и y=3sin(0.5w t) (смещение из положения равновесия – в метрах, время – в секундах). Определить траекторию точки. 210. Складываются два колебания одного направления и одной частоты: x1=sin(pt) x2=sin(p(t+0.5)) (смещение из положения равновесия - в метрах, время – в секундах). Определить амплитуду и начальную фазу результирующего колебания, написать уравнение колебания. 211. Маленькое тело совершает колебания x=2sin(0.25pt-0.5p) (смещение из положения равновесия - в метрах, время – в секундах). Найти амплитуду, период, начальную фазу, максимальную скорость и максимальное ускорение тела. 212. Точка колеблется гармонически по закону косинуса. Амплитуда колебаний 5 см, круговая частота 2 рад/с, начальная фаза равна нулю. Определить ускорение точки в момент, когда величина ее скорости равна 8 см/с. Записать уравнение колебаний. 213. Точка совершает гармонические колебания по закону синуса. В некоторый момент времени смещение точки было равно 7 см. При увеличении фазы вдвое смещение точки стало 12 см. Найти амплитуду колебаний. 214. Через какой промежуток времени после начала колебаний смещение точки из положения равновесия будет равно половине амплитуды, если период колебаний 24 с, начальная фаза равна нулю, а колебания происходят по закону косинуса? 215. Период колебаний материальной точки 2.4 с, амплитуда 5 см, начальная фаза равна нулю. Найти смещение, скорость и ускорение колеблющейся точки через 0.4 с после начала колебаний. Колебания происходят по закону косинуса. 216. Написать уравнение гармонических колебаний, если максимальное ускорение точки 49.3 см/с2, период колебаний 2 с, смещение точки из положения равновесия в начальный момент времени 25 мм. 217. Точка совершает гармонические колебания по закону косинуса. В некоторый момент времени смещение точки 5 см, ее скорость 20 см/с, ускорение равно 80 см/с2. Найти циклическую частоту, амплитуду и период колебаний, фазу колебаний в рассматриваемый момент времени. 218. Амплитуда колебаний материальной точки массой 3 г равна 15 см, круговая частота 10 рад/с. Определить максимальную величину возвращающей силы и максимальную кинетическую энергию точки. 219. На тело, совершающее гармонические колебания с периодом 1 с и начальной фазой p/6, действует максимальная возвращающая сила 17.5 Н. При этом полная энергия колебаний 2.85 Дж. Написать уравнение колебаний. Колебания происходят по закону косинуса. 220. Материальная точка массой 10 г совершает гармонические колебания, уравнение которых имеет вид: x=0.2sin(8pt) (смещение из положения равновесия - в метрах, время – в секундах). Найти значение возвращающей силы в момент времени 0.1 с и кинетическую энергию точки в данный момент времени. 221. Материальная точка совершает гармонические колебания, уравнение которых имеет вид: x=0.1sin(5pt) (смещение из положения равновесия - в метрах, время – в секундах). Масса точки 50 г. Найти силу, действующую на точку: 1) в тот момент, когда фаза колебаний равна 300; 2) в положении наибольшего отклонения точки. 222. Математический маятник массой 100 г совершает гармонические колебания по закону x=0.25sin(2pt) (смещение из положения равновесия - в метрах, время – в секундах). Определить натяжение нити в момент времени t=T/2. 223. Точка совершает гармонические колебания, уравнение которых имеет вид: x=0.05sin(2t) (смещение из положения равновесия - в метрах, время – в секундах). В момент, когда на точку действовала возвращающая сила 5 мН, точка обладала потенциальной энергией 0.1 мДж. Найти фазу колебаний в этот момент времени. 224. Определить период колебаний груза массой 5 кг, подвешенного к пружине, если пружина под действием силы в 40 Н растягивается на 6 см. 225. Логарифмический декремент затухания математического маятника равен 0.2. Найти, во сколько раз уменьшится амплитуда колебаний за одно полное колебание, то есть за время t=T. 226. Чему равен логарифмический декремент затухания математического маятника, если за 1 минуту амплитуда колебаний уменьшилась в два раза? Длина маятника 1 м. 227. Логарифмический декремент затухания колебаний маятника равен 0.003. Сколько полных колебаний должен сделать маятник, чтобы амплитуда уменьшилась в 2 раза? 228. Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 731 Гц? 229. Сферическая волна распространяется от источника колебаний вдоль прямой OX. Смещение точки из положения равновесия для момента времени t=T/2 составляет 5 см. Точка удалена от источника колебаний на расстояние, равное l /3. Определить амплитуду колебаний. Колебания источника происходят по закону косинуса. 230. Плоская волна с периодом 1.2 с и амплитудой 2 см распространяется со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 45 м от источника волн в тот момент, когда от начала колебаний источника прошло 4 с? 231. Плоская звуковая волна распространяется в воздухе при н.у. вдоль прямой со скоростью 20 м/с. Две точки, находящиеся на этой прямой на расстоянии 12 м и 15 м от источника, колеблются с разностью фаз 0.75p. Найти длину волны, написать уравнение волны и найти смещение обеих указанных точек в момент времени, равный 1.2 с, если амплитуда колебаний 10 см. 232. Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника колебаний, колеблющегося по закону: x=sin(ωt),в момент времени t=T/6 равно половине амплитуды. Найти длину волны. Волна плоская. 233. Уравнение незатухающих колебаний дано в виде x=sin(2.5pt) (смещение из положения равновесия - в см, время – в секундах). Найти смещение от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20 см от источника колебаний, для момента времени 1 с после начала колебаний. Скорость распространения волны 100 м/с. Волна плоская. 234. К неподвижной опоре подвесили пружину жесткостью К =100 Н/м с грузом массой m=50 г. Пружину растянули на 10 см и, отпуская, подтолкнули вдоль оси пружины в направлении положения равновесия, сообщив грузу скорость υ0=2 м/с. Далее пружина с грузом предоставлены сами себе. Записать уравнение колебаний, определить амплитуду колебаний. Сопротивлением среды пренебречь. 235. Груз массой m подвешен к системе двух последовательно соединенных пружин жесткостями K 1 и K 2. Система выведена из состояния равновесия и предоставлена сама себе. Энергия, сообщенная системе, равна W. Написать уравнение колебаний, определить амплитуду и частоту колебаний. Сопротивлением среды пренебречь. 236. Два точечных источника колебаний, отстоящие на расстоянии d =10 м друг от друга, колеблются по одинаковому закону y=0.25sin(8pt) (смещение из положения равновесия - в метрах, время – в секундах). Написать уравнение колебаний в точке А, лежащей на продолжении прямой, соединяющей первый источник со вторым, на расстоянии х =7 м от второго. Скорость распространения плоских волн равна скорости звука в воздухе при нормальных условиях. 237. Найти модуль Юнга металла, если скорость звука в нем υ= 4700 м/с, а его плотность ρ=8.6.103 кг/м3. 238. Определить разность фаз колебаний двух точек среды, находящихся на расстоянии 0.1 м друг от друга, если в среде распространяется плоская волна вдоль линии, соединяющей эти точки. Скорость распространения волны υ=340 м/с, частота колебаний источника 1000 Гц. 239.
240. Два точечных когерентных источника звуковых волн одинаковой мощности находятся в воздухе при н.у. на расстояниях l 1=2.5 м и l 2=2.4 м от микрофона. Определить отношение амплитуд результирующего и исходного колебаний, если длина волны λ=0.3м. 241. На вертикально отклоняющие пластины осциллографа подаются два одинаково направленных колебания: Uy1=10sin(ωt-π/6), и Uy2=5cos(ωt), на горизонтально отклоняющие Uх=8.66cos(ωt) (напряжение – в вольтах, время – в секундах). Определить траекторию луча на экране. 242. Обруч диаметром 56.5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период этих колебаний. 243. Начальная фаза колебаний точки равна π/3, период колебаний Т=0.06 с. Определить ближайшие моменты времени, в которые модули скорости и ускорения в 2 раза меньше амплитудных значений. Колебания происходят по закону синуса. 244. При сложении двух одинаково направленных гармонических колебаний с одинаковой частотой и амплитудами, равными 0.02 и 0.04 м, получается гармоническое колебание с амплитудой 0.05 м. Найти разность фаз складываемых колебаний. 245. На тонкой нити длиной 1 м подвешен шар радиуса r=0.1 м. Определить относительную погрешность в определении периода колебаний, если маятник считать математическим. 246. Период затухающих колебаний 4 с, логарифмический декремент затухания 1.6, начальная фаза равна нулю. Смещение точки из положения равновесия в момент времени t=T/4 равно 4.5 см. Написать уравнение этого колебания. 247. Для звуковой волны, описываемой уравнением 248. Период колебаний крутильного маятника, состоящего из тонкого кольца массой 5.10-2 кг, соединенного спиральной пружиной с осью вращения, равен Т=4 с. Определить радиус кольца при жесткости пружины K =10-2 Н.м. Трением пренебречь. 249. Начальная амплитуда колебаний математического маятника А 0=0.2 м. Амплитуда после 10 полных колебаний А 10=0.01 м. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний Т=5 с. Записать уравнение колебаний. 250. Математический маятник массой m =0.10 кг совершает гармонические колебания по закону y=0.5sin(2πt) (смещение из положения равновесия - в м, время – в секундах). Определить натяжение нити в момент времени t=Т/2. 251. Как изменится период вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от последовательного соединения пружин перейти к их параллельному соединению? 252. На концах вертикального стержня укреплены два груза. Центр тяжести этих грузов находится ниже середины стержня на 5 см. Найти длину стержня, если период малых колебаний стержня с грузами вокруг горизонтальной оси, проходящей через его середину, равен 2 с. Массой стержня по сравнению с массой грузов пренебречь. 253. Тело движется под действием силы F=fcos(ωt) по закону x=Сsin(ωt) (f =2 Н, С =10 см, ω=π/3 рад/с). Найти работу силы за время от t=0 до t=20 с. Найти работу силы и ее среднюю мощность за время t=Т. 254. На тело массой m действует сила, изменяющаяся по закону F=Аcos(ωt), где А =2 Н, ω=π/3 рад/с. Найти закон движения тела x (t) при условии, что в начальный момент времени смещение из положения равновесия и начальная скорость равны нулю. Установить, что такое движение является колебательным. Определить период колебаний, наибольшее значение x и наибольшее значение скорости. 255. Однородный стержень совершает малые колебания в вертикальной плоскости около горизонтальной оси, проходящей через его верхний конец. Длина стержня 50 см. Найти период колебаний стержня. 256. Ось вращения стержня проходит на расстоянии 10 см от его конца. Длина стержня 50 см. Найти период малых колебаний. 257. Обруч диаметром 56.5 см висит на гвозде, вбитом в стену, и совершает малые колебания в плоскости, параллельной стене. Найти период колебаний обруча. 258. Какой наименьшей длины надо взять нить, к которой подвешен однородный шарик диаметром 4 см, чтобы при определении периода малых колебаний шарика можно было рассматривать его как математический маятник? Ошибка при таком допущении не должна превышать 1%. 259. Стальная полоска зажата с одного конца и расположена горизонтально. На другом конце полоски закрепляют груз, масса которого значительно больше массы полоски. При наличии груза полоска изгибается и ее не зажатый конец опускается на 4 см. С какой частотой будет колебаться груз, если его толкнуть в вертикальном направлении? С каким ускорением будет двигаться колеблющийся груз в тот момент, когда полоска полностью выпрямится? 260. Шарик подвешен на длинной нити. Один раз его поднимают по вертикали до точки подвеса, другой раз – отклоняют, как маятник, на небольшой угол. В каком случае и во сколько раз шарик быстрее возвратится к начальному положению, если его отпустить? 261. Маятник в виде грузика, подвешенного на нити длиной 50 см, колеблется в кабине самолета. Каков период его колебаний, если самолет: а) движется равномерно; б) движется горизонтально с ускорением 2.5 м/с2; в) планирует вниз под углом 150 к горизонту (лобовым сопротивлением самолета пренебречь)? 262. Маятник в виде маленького шарика, подвешенного на нити длиной 10 см, находится внутри жидкости, плотность которой в n=1.2 раза меньше плотности шарика. Определите период колебаний маятника, пренебрегая сопротивлением жидкости и принимая, что эффективная масса при движении шарика в жидкости увеличивается на величину, равную массе вытесненной жидкости. 263. Маятник представляет собой очень легкий стержень длиной 45 см, на концах которого закреплены два одинаковых груза – один на расстоянии 30 см от оси, другой на расстоянии 15 см от оси. Найти период колебаний такого маятника. 264. Однородный диск радиусом R подвешен за край. Чему равна частота его малых колебаний относительно точки подвеса?
Механика жидкостей и газов.
265. Бак высотой 1.5 м наполнен до краев водой. На расстоянии 1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии от бака падает на пол струя, вытекая из отверстия? 266. Площадь соприкосновения слоев текущей жидкости 10 см2, коэффициент динамической вязкости жидкости равен 10-3 Па×с, а возникающая сила трения между слоями 0.1 мН. Определить градиент скорости. 267. Бак высотой 2 м до краев наполнен жидкостью. На какой высоте должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном от бака расстоянии? 268. В дне цилиндрического сосуда диаметром 50 см имеется круглое отверстие диаметром 1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты этого уровня. Найти значение этой скорости при высоте уровня воды 20 см. 269. В сосуд льется вода, причем за 1 с наливается объем воды 0.2 л. Каким должен быть диаметр отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне 8.3 см? 270. В боковую поверхность цилиндрического сосуда радиусом 2 см вставлен горизонтальный капилляр, внутренний радиус которого равен 1 мм и длина 1.5 см. В сосуд налито касторовое масло, вязкость которого 1.2 Па.с, плотность – 970 кг/м3. Найти зависимость скорости понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h=26 см. 271. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте 5 см от дна сосуда. Внутренний радиус капилляра равен 1 мм и длина 1 см. В сосуд налито машинное масло, вязкость которого 0.5 Па.с, а плотность 900 кг/м3. Уровень масла в сосуде поддерживается постоянным на высоте 50 см выше капилляра. На каком расстоянии от конца капилляра по горизонтали струя масла падает на стол? 272. Считая, что ламинарность движения жидкости или газа в цилиндрической трубе сохраняется при числе Рейнольдса Re<3000 (если в качестве d взять диаметр трубы), показать, что при кинематической вязкости газа 1.33.10-6 м2/с, текущего по трубе диаметром 2 см, течение будет ламинарным. Плотность газа 7.5 кг/м3. За 30 мин через поперечное сечение трубы протекает 0.51 кг газа. Газ считать несжимаемым. 273. Латунный шарик диаметром 0.5 мм падает в глицерине. Определить 1) скорость установившегося движения шарика; 2) является ли при этом значении скорости обтекание шарика ламинарным? Плотность латуни и глицерина 8.55×103 кг/м3 и 1.26×103 кг/м3 соответственно; динамическая вязкость глицерина 1.48 Па×с. Критическое значение числа Рейнольдса при падении шарика принять равным 0.5. 274. Свинцовая пуля в виде шарика диаметром 5 мм движется в воздухе. Принимая плотность воздуха равной 0.0012 г/см3, определите число Рейнольдса, если мгновенная скорость пули равна 300 м/с. С каким ускорением движется при этой скорости пуля? Массой вытесненного воздуха и наличием поля тяготения пренебречь. Принять, что при турбулентном обтекании твердого тела сила лобового сопротивления вычисляется по формуле F=cS v2 ρ, где безразмерный коэффициент c для шараравен 0.25, S – наибольшая площадь сечения тела в направлении, перпендикулярном скорости v, ρ – плотность среды. Динамическая вязкость воздуха 1.72.10-5Па.с, плотность свинца 11300 кг/м3. 275. На тележке стоит цилиндрический сосуд, наполненный водой. Высота воды в сосуде 1 м. В сосуде с противоположных сторон по ходу тележки сделано два крана с отверстиями площадью 10 см2 каждое, одно на высоте 0.25 м над дном сосуда, а другое на высоте 0.5 м. Какую горизонтальную силу нужно приложить к тележке, чтобы она осталась в покое при открытых кранах? 276. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы 0.2 м/с. Определить скорость в узкой части трубы, диаметр которой в 1.5 раза меньше диаметра широкой части трубы. 277. В широкой части горизонтально расположенной трубы нефть течет со скоростью 2 м/с. Определить скорость нефти в узкой части, если разность давлений в широкой и узкой частях ее равна 6.65 кПа. Плотность нефти 0.9×103 кг/м3. 278. В горизонтально расположенной трубе с площадью поперечного сечения 20 см2 течет вода. В одном месте труба имеет сужение, в котором площадь сечения 12 см2. Разность уровней воды в двух манометрических трубках, установленных в широкой и узкой частях трубы, равна 8 см. Определить объемный расход жидкости. 279. Горизонтальный цилиндр насоса имеет диаметр 5 см. В нем движется со скоростью 1 м/с поршень, выталкивая воду через отверстие диаметром 2 см. С какой скоростью будет двигаться вода из отверстия? Каково будет избыточное давление воды в цилиндре? 280. К поршню шприца, расположенного горизонтально, приложена сила 15 Н. Определить скорость истечения воды из наконечника шприца, если площадь поршня 2 см2. 281. Струя воды с площадью поперечного сечения 4 см2 вытекает в горизонтальном направлении из брандспойта, расположенного на высоте 2 м над поверхностью Земли, и падает на эту поверхность на расстоянии 8 м. Пренебрегая сопротивлением воздуха движению воды, найти избыточнее давление воды в рукаве, если площадь поперечного сечения рукава 50 см2. 282. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии h1 от дна сосуда и на расстоянии h2 от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии от сосуда (по горизонтали) струя воды падает на стол в случаях: 1) h1=25 см, h2=16 см; 2) h1=16 см, h2=25 см? 283. Какое давление создает компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью 25 м/с? Плотность краски 800 кг/м3. 284. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого равен 1 мм и длина 1.5 см. В сосуд налит глицерин, вязкость которого 1.0 Па.с, плотность 1260 кг/м3. Уровень глицерина в сосуде поддерживается постоянным на высоте 18 см выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина 5 мл? 285. Вода течет по круглой гладкой трубе диаметром 5 см со средней по сечению скоростью 0.1 м/с. Определить число Рейнольдса для потока жидкости в трубе и указать характер течения жидкости, если критическое значение числа Рейнольдса для водных систем 2000, а коэффициент динамической вязкости воды 0.001 Па×с. 286. По трубе течет машинное масло. Максимальная скорость, при которой движение масла в трубе остается еще ламинарным, равна 3.2×10-2 м/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного в турбулентное? Коэффициент динамической вязкости машинного масла и глицерина 0.5 Па×с и 1.48 Па×с соответственно, а плотности 0.9×103 кг/м3 и 1.26×103 кг/м3. 287. Вода течет по круглой гладкой трубе диаметром 6 см со скоростью 10 см/с. Чему равно для этого потока воды в трубе число Рейнольдса? Каков характер движения воды? Вязкость воды 0.001 Па.с. 288. Вода течет по трубе, причем за 1 с через поперечное сечение трубы протекает объем воды 200 мл. Динамическая вязкость воды 0.001 Па.с. При каком предельном значении диаметра трубы движение воды остается ламинарным? Ламинарность движения жидкости или газа в цилиндрической трубе сохраняется при числе Рейнольдса Re<3000. 289. При движении шарика радиусом 2.4 мм в касторовом масле ламинарное обтекание наблюдается при скорости, не превышающей 10 см/с. При какой минимальной скорости шарика радиусом 1 мм в глицерине обтекание станет турбулентным? Плотность касторового масла и глицерина 0.96×103 кг/м3 и 1.26×103 кг/м3; динамическая вязкость 0.987 Па×с и 1.48 Па×с соответственно. 290. Какой наибольшей скорости может достичь дождевая капля диаметром 0.3 мм, если динамическая вязкость воздуха 1.72.10-5Па.с? 291. Стальной шарик диаметром 1 мм падает с постоянной скоростью 0.185см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость масла. Плотности стали и масла 7800 кг/м3 и 900 кг/м3 соответственно. 292. Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом, с постоянной скоростью 3.5 см/с. Найти динамическую и кинематическую вязкость масла, если плотность масла и пробки 900 кг/м3 и 200 кг/м3 соответственно. 293. Стальной шарик падает в широком сосуде с трансформаторным маслом, плотность которого 900 кг/м3 и динамическая вязкость 0.8 Па.с. Считая, что закон Стокса имеет место при числе Рейнольдса Re<0.5 (если при вычислении Re в качестве d взять диаметр шарика), найти предельное значение диаметра шарика. Плотность стали 7800 кг/м3. 294. Медный шарик диаметром 1 см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса при падении шарика принять равным 0.5. Плотность меди и касторового масла 8900 кг/м3 и 900 кг/м3 соответственно; динамическая вязкость касторового масла 1.2 Па×с. 295. В восходящем потоке воздуха, скорость которого 2 см/с, находится пылинка, имеющая форму шарика диаметром 0.01 мм. Опускается или поднимается пылинка, если ее плотность на 2.3 г/см3 больше плотности воздуха? Принять, что движение воздуха при обтекании пылинки является ламинарным. Вязкость воздуха 1.72.10-5Па.с. Библиографический список
1. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С.Волькенштейн. – СПб.: Лань, 1999. – 328 с. 2. Иродов, И.Е. Задачи по общей физике: учебное пособие / И.Е.Иродов. – СПб.: Лань, 2001. – 416 с. 3. Калашников, Н.П. Основы физики: учеб. для вузов: в 2 т. / Н.П.Калашников, М.А.Смондырев. - 2-е изд., перераб. – М.: Дрофа, 2003. 4. Детлаф, А.А. Курс физики: учеб. пособие для вузов / А.А. Детлаф, В.М. Яворский. - М.: Высш.шк., 1989.- 608 с. 5. Курс физики: учеб. для вузов: в 2 т. Т. 1 / под ред. В.Н.Лозовского. – СПб.: Лань, 2000. – 576 с. 6. Трофимова, Т.И. Курс физики/ Т.И. Трофимова.-М.: Высш. шк., 1999.-542 с.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 ;
;  ;
;  – смещение из положения равновесия, скорость и ускорение колеблющейся точки;
– смещение из положения равновесия, скорость и ускорение колеблющейся точки; – дифференциальное уравнение гармонических колебаний;
– дифференциальное уравнение гармонических колебаний; – возвращающая сила при гармонических колебаниях;
– возвращающая сила при гармонических колебаниях; ;
; 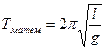 ;
;  ;
;  (здесь
(здесь 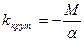 – модуль кручения) – период колебаний пружинного, математического, физического и крутильного маятников;
– модуль кручения) – период колебаний пружинного, математического, физического и крутильного маятников; ;
;  – закон сохранения энергии;
– закон сохранения энергии; ;
;  – амплитуда и начальная фаза результирующего колебания при сложении однонаправленных колебаний одинаковой частоты;
– амплитуда и начальная фаза результирующего колебания при сложении однонаправленных колебаний одинаковой частоты;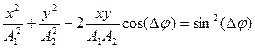 – уравнение траектории точки, колеблющейся с одинаковыми частотами в перпендикулярных направлениях;
– уравнение траектории точки, колеблющейся с одинаковыми частотами в перпендикулярных направлениях; – дифференциальное уравнение затухающих колебаний;
– дифференциальное уравнение затухающих колебаний;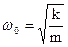 – круговая частота собственных незатухающих колебаний;
– круговая частота собственных незатухающих колебаний;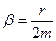 – коэффициент затухания;
– коэффициент затухания; – сила сопротивления при затухающих колебаниях;
– сила сопротивления при затухающих колебаниях;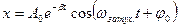 – уравнение затухающих колебаний;
– уравнение затухающих колебаний; – круговая частота затухающих колебаний;
– круговая частота затухающих колебаний; – амплитуда затухающих колебаний;
– амплитуда затухающих колебаний; – логарифмический декремент затухания;
– логарифмический декремент затухания; – добротность;
– добротность; (здесь
(здесь  ) – дифференциальное уравнение вынужденных колебаний;
) – дифференциальное уравнение вынужденных колебаний; ;
;  ;
;  – смещение из положения равновесия, амплитуда и фаза вынужденных колебаний;
– смещение из положения равновесия, амплитуда и фаза вынужденных колебаний;  – резонансная частота;
– резонансная частота; ,
,  – уравнения плоской и сферической волн;
– уравнения плоской и сферической волн; – волновое число (волновой вектор);
– волновое число (волновой вектор);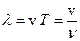 – длина волны;
– длина волны; ;
; 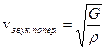 – скорость распространения продольных и поперечных волн в твердом теле;
– скорость распространения продольных и поперечных волн в твердом теле;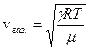 – скорость звука в газе;
– скорость звука в газе; – скорость распространения поперечной волны по струне.
– скорость распространения поперечной волны по струне.
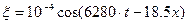 , где амплитуда выражена в метрах, круговая частота – в с-1, волновое число – в м-1, найти: а) амплитуду скорости частиц среды и ее отношение к скорости распространения волны; б) отношение амплитуды смещения частиц среды к длине волны.
, где амплитуда выражена в метрах, круговая частота – в с-1, волновое число – в м-1, найти: а) амплитуду скорости частиц среды и ее отношение к скорости распространения волны; б) отношение амплитуды смещения частиц среды к длине волны. – уравнение неразрывности;
– уравнение неразрывности; – давление;
– давление; – гидростатическое давление;
– гидростатическое давление; – закон Архимеда;
– закон Архимеда; – уравнение Бернулли;
– уравнение Бернулли; – сила вязкого трения между слоями жидкости или газа;
– сила вязкого трения между слоями жидкости или газа; – кинематическая вязкость;
– кинематическая вязкость; – число Рейнольдса;
– число Рейнольдса; – закон Стокса;
– закон Стокса; – объемный расход;
– объемный расход; – формула Пуазейля.
– формула Пуазейля.


