
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Групп зпгс-11,12 , зса-11, зтгв-11.Стр 1 из 6Следующая ⇒
Динамика вращательного движения. Работа, энергия. Механика жидкостей и газов.
265. Бак высотой 1.5 м наполнен до краев водой. На расстоянии 1 м от верхнего края бака образовалось отверстие малого диаметра. На каком расстоянии от бака падает на пол струя, вытекая из отверстия? 266. Площадь соприкосновения слоев текущей жидкости 10 см2, коэффициент динамической вязкости жидкости равен 10-3 Па×с, а возникающая сила трения между слоями 0.1 мН. Определить градиент скорости. 267. Бак высотой 2 м до краев наполнен жидкостью. На какой высоте должно быть проделано отверстие в стенке бака, чтобы место падения струи, вытекающей из отверстия, было на максимальном от бака расстоянии? 268. В дне цилиндрического сосуда диаметром 50 см имеется круглое отверстие диаметром 1 см. Найти зависимость скорости понижения уровня воды в сосуде от высоты этого уровня. Найти значение этой скорости при высоте уровня воды 20 см. 269. В сосуд льется вода, причем за 1 с наливается объем воды 0.2 л. Каким должен быть диаметр отверстия в дне сосуда, чтобы вода в нем держалась на постоянном уровне 8.3 см? 270. В боковую поверхность цилиндрического сосуда радиусом 2 см вставлен горизонтальный капилляр, внутренний радиус которого равен 1 мм и длина 1.5 см. В сосуд налито касторовое масло, вязкость которого 1.2 Па.с, плотность – 970 кг/м3. Найти зависимость скорости понижения уровня касторового масла в сосуде от высоты h этого уровня над капилляром. Найти значение этой скорости при h=26 см. 271. На столе стоит сосуд, в боковую поверхность которого вставлен горизонтальный капилляр на высоте 5 см от дна сосуда. Внутренний радиус капилляра равен 1 мм и длина 1 см. В сосуд налито машинное масло, вязкость которого 0.5 Па.с, а плотность 900 кг/м3. Уровень масла в сосуде поддерживается постоянным на высоте 50 см выше капилляра. На каком расстоянии от конца капилляра по горизонтали струя масла падает на стол? 272. Считая, что ламинарность движения жидкости или газа в цилиндрической трубе сохраняется при числе Рейнольдса Re<3000 (если в качестве d взять диаметр трубы), показать, что при кинематической вязкости газа 1.33.10-6 м2/с, текущего по трубе диаметром 2 см, течение будет ламинарным. Плотность газа 7.5 кг/м3. За 30 мин через поперечное сечение трубы протекает 0.51 кг газа. Газ считать несжимаемым.
273. Латунный шарик диаметром 0.5 мм падает в глицерине. Определить 1) скорость установившегося движения шарика; 2) является ли при этом значении скорости обтекание шарика ламинарным? Плотность латуни и глицерина 8.55×103 кг/м3 и 1.26×103 кг/м3 соответственно; динамическая вязкость глицерина 1.48 Па×с. Критическое значение числа Рейнольдса при падении шарика принять равным 0.5. 274. Свинцовая пуля в виде шарика диаметром 5 мм движется в воздухе. Принимая плотность воздуха равной 0.0012 г/см3, определите число Рейнольдса, если мгновенная скорость пули равна 300 м/с. С каким ускорением движется при этой скорости пуля? Массой вытесненного воздуха и наличием поля тяготения пренебречь. Принять, что при турбулентном обтекании твердого тела сила лобового сопротивления вычисляется по формуле F=cS v2 ρ, где безразмерный коэффициент c для шараравен 0.25, S – наибольшая площадь сечения тела в направлении, перпендикулярном скорости v, ρ – плотность среды. Динамическая вязкость воздуха 1.72.10-5Па.с, плотность свинца 11300 кг/м3. 275. На тележке стоит цилиндрический сосуд, наполненный водой. Высота воды в сосуде 1 м. В сосуде с противоположных сторон по ходу тележки сделано два крана с отверстиями площадью 10 см2 каждое, одно на высоте 0.25 м над дном сосуда, а другое на высоте 0.5 м. Какую горизонтальную силу нужно приложить к тележке, чтобы она осталась в покое при открытых кранах? 276. Вода течет в горизонтально расположенной трубе переменного сечения. Скорость воды в широкой части трубы 0.2 м/с. Определить скорость в узкой части трубы, диаметр которой в 1.5 раза меньше диаметра широкой части трубы. 277. В широкой части горизонтально расположенной трубы нефть течет со скоростью 2 м/с. Определить скорость нефти в узкой части, если разность давлений в широкой и узкой частях ее равна 6.65 кПа. Плотность нефти 0.9×103 кг/м3.
278. В горизонтально расположенной трубе с площадью поперечного сечения 20 см2 течет вода. В одном месте труба имеет сужение, в котором площадь сечения 12 см2. Разность уровней воды в двух манометрических трубках, установленных в широкой и узкой частях трубы, равна 8 см. Определить объемный расход жидкости. 279. Горизонтальный цилиндр насоса имеет диаметр 5 см. В нем движется со скоростью 1 м/с поршень, выталкивая воду через отверстие диаметром 2 см. С какой скоростью будет двигаться вода из отверстия? Каково будет избыточное давление воды в цилиндре? 280. К поршню шприца, расположенного горизонтально, приложена сила 15 Н. Определить скорость истечения воды из наконечника шприца, если площадь поршня 2 см2. 281. Струя воды с площадью поперечного сечения 4 см2 вытекает в горизонтальном направлении из брандспойта, расположенного на высоте 2 м над поверхностью Земли, и падает на эту поверхность на расстоянии 8 м. Пренебрегая сопротивлением воздуха движению воды, найти избыточнее давление воды в рукаве, если площадь поперечного сечения рукава 50 см2. 282. На столе стоит сосуд с водой, в боковой поверхности которого имеется малое отверстие, расположенное на расстоянии h1 от дна сосуда и на расстоянии h2 от уровня воды. Уровень воды в сосуде поддерживается постоянным. На каком расстоянии от сосуда (по горизонтали) струя воды падает на стол в случаях: 1) h1=25 см, h2=16 см; 2) h1=16 см, h2=25 см? 283. Какое давление создает компрессор в краскопульте, если струя жидкой краски вытекает из него со скоростью 25 м/с? Плотность краски 800 кг/м3. 284. В боковую поверхность сосуда вставлен горизонтальный капилляр, внутренний радиус которого равен 1 мм и длина 1.5 см. В сосуд налит глицерин, вязкость которого 1.0 Па.с, плотность 1260 кг/м3. Уровень глицерина в сосуде поддерживается постоянным на высоте 18 см выше капилляра. Какое время потребуется на то, чтобы из капилляра вытек объем глицерина 5 мл? 285. Вода течет по круглой гладкой трубе диаметром 5 см со средней по сечению скоростью 0.1 м/с. Определить число Рейнольдса для потока жидкости в трубе и указать характер течения жидкости, если критическое значение числа Рейнольдса для водных систем 2000, а коэффициент динамической вязкости воды 0.001 Па×с. 286. По трубе течет машинное масло. Максимальная скорость, при которой движение масла в трубе остается еще ламинарным, равна 3.2×10-2 м/с. При какой скорости движение глицерина в той же трубе переходит из ламинарного в турбулентное? Коэффициент динамической вязкости машинного масла и глицерина 0.5 Па×с и 1.48 Па×с соответственно, а плотности 0.9×103 кг/м3 и 1.26×103 кг/м3. 287. Вода течет по круглой гладкой трубе диаметром 6 см со скоростью 10 см/с. Чему равно для этого потока воды в трубе число Рейнольдса? Каков характер движения воды? Вязкость воды 0.001 Па.с. 288. Вода течет по трубе, причем за 1 с через поперечное сечение трубы протекает объем воды 200 мл. Динамическая вязкость воды 0.001 Па.с. При каком предельном значении диаметра трубы движение воды остается ламинарным? Ламинарность движения жидкости или газа в цилиндрической трубе сохраняется при числе Рейнольдса Re<3000. 289. При движении шарика радиусом 2.4 мм в касторовом масле ламинарное обтекание наблюдается при скорости, не превышающей 10 см/с. При какой минимальной скорости шарика радиусом 1 мм в глицерине обтекание станет турбулентным? Плотность касторового масла и глицерина 0.96×103 кг/м3 и 1.26×103 кг/м3; динамическая вязкость 0.987 Па×с и 1.48 Па×с соответственно.
290. Какой наибольшей скорости может достичь дождевая капля диаметром 0.3 мм, если динамическая вязкость воздуха 1.72.10-5Па.с? 291. Стальной шарик диаметром 1 мм падает с постоянной скоростью 0.185см/с в большом сосуде, наполненном касторовым маслом. Найти динамическую вязкость масла. Плотности стали и масла 7800 кг/м3 и 900 кг/м3 соответственно. 292. Пробковый шарик радиусом 5 мм всплывает в сосуде, наполненном касторовым маслом, с постоянной скоростью 3.5 см/с. Найти динамическую и кинематическую вязкость масла, если плотность масла и пробки 900 кг/м3 и 200 кг/м3 соответственно. 293. Стальной шарик падает в широком сосуде с трансформаторным маслом, плотность которого 900 кг/м3 и динамическая вязкость 0.8 Па.с. Считая, что закон Стокса имеет место при числе Рейнольдса Re<0.5 (если при вычислении Re в качестве d взять диаметр шарика), найти предельное значение диаметра шарика. Плотность стали 7800 кг/м3. 294. Медный шарик диаметром 1 см падает с постоянной скоростью в касторовом масле. Является ли движение масла, вызванное падением в нем шарика, ламинарным? Критическое значение числа Рейнольдса при падении шарика принять равным 0.5. Плотность меди и касторового масла 8900 кг/м3 и 900 кг/м3 соответственно; динамическая вязкость касторового масла 1.2 Па×с. 295. В восходящем потоке воздуха, скорость которого 2 см/с, находится пылинка, имеющая форму шарика диаметром 0.01 мм. Опускается или поднимается пылинка, если ее плотность на 2.3 г/см3 больше плотности воздуха? Принять, что движение воздуха при обтекании пылинки является ламинарным. Вязкость воздуха 1.72.10-5Па.с. Библиографический список
1. Волькенштейн, В.С. Сборник задач по общему курсу физики / В.С.Волькенштейн. – СПб.: Лань, 1999. – 328 с. 2. Иродов, И.Е. Задачи по общей физике: учебное пособие / И.Е.Иродов. – СПб.: Лань, 2001. – 416 с. 3. Калашников, Н.П. Основы физики: учеб. для вузов: в 2 т. / Н.П.Калашников, М.А.Смондырев. - 2-е изд., перераб. – М.: Дрофа, 2003. 4. Детлаф, А.А. Курс физики: учеб. пособие для вузов / А.А. Детлаф, В.М. Яворский. - М.: Высш.шк., 1989.- 608 с. 5. Курс физики: учеб. для вузов: в 2 т. Т. 1 / под ред. В.Н.Лозовского. – СПб.: Лань, 2000. – 576 с. 6. Трофимова, Т.И. Курс физики/ Т.И. Трофимова.-М.: Высш. шк., 1999.-542 с.
групп ЗПГС-11,12, ЗСА-11, ЗТГВ-11. Требования к оформлению и общие методические указания по выполнению контрольной работы.
1. Номер варианта совпадает с последней цифрой в зачетке. 2. Номера задач в зависимости от номера варианта определяются по формуле: Nзадачи=30n+Nварианта, где n=0, 1, …12. Например, последняя цифра в зачетке 5, тогда ваши задачи: 30*0+5=5 и т.д, 35, 65, 95….. 3. Задачи оформляются в письменном виде. Решение каждой задачи необходимо начинать с новой страницы. 4. Требуется указать номер варианта и номер задачи по нумерации пособия. 5. Условие задачи переписывается полностью, без сокращений. 6. Решение записывается в стандартном виде:
7. Все физические величины необходимо выразить в системе единиц СИ. 8. Сделать рисунок, схему, если это необходимо. 9. Сформулировать основные законы, записать формулы, на которых базируется решение. Обосновать возможность их применения в условиях данной задачи. Составить полную систему уравнений для решения задачи. 10.Получить окончательное выражение искомой величины в общем виде. Проверить размерность. 11.Подставить числовые данные и рассчитать искомую величину. 12.Проанализировать полученный результат. 13.Записать ответ. 14.Каждую задачу требуется защитить, то есть полностью объяснить решение задачи преподавателю. 1. Кинематика поступательного движения.
v ср .=
v= v х =
aх =
Равнопеременное движение (
1. Движение двух материальных точек выражается уравнениями: x1=20+2t–4t3 и x2=2+2t+0.5t3 (координаты в метрах, время в секундах). В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент? 2. Первую треть пути автомобиль проехал со скоростью 10 км/ч, вторую треть со скоростью 20 км/ч и последнюю треть – со скоростью 60 км/ч. Определить среднюю скорость движения автомобиля. 3. Тело начинает падать со скоростью 16 м/с, находясь на высоте 200 м. Определить, через сколько времени тело достигнет земли, если начальная скорость направлена: а) вверх; б) вниз. Доказать, что скорость приземления в обоих случаях одинакова. 4. Тело свободно падает и последние 196 м пути проходит за 4 секунды. Сколько времени падало тело? Чему равна высота? 5. Тело брошено под углом 300 к горизонту. С какой скоростью было брошено тело и какова горизонтальная дальность его полета, если оно находилось в полете 2 с? Какова максимальная высота подъема тела? 6. С какой скоростью должен лететь самолет и какой курс он должен держать, чтобы за 1 час пролететь точно по направлению на север путь 200 км, если во время полета дует северо-восточный ветер под углом 350 к меридиану со скоростью 30 км/час?
7. Свободно падающее тело в последнюю секунду своего падения проходит половину всего пути. Найти, с какой высоты падает тело; продолжительность его падения. 8. Поезд, двигаясь от остановки, прошел 200 м в течение 50 с и достиг скорости 6 м/с. Увеличивалось или уменьшалось ускорение движения с течением времени? 9. Фонарь, находящийся на расстоянии 3 м от вертикальной стены, бросает на нее световой «зайчик». Фонарь равномерно вращается вокруг вертикальной оси с частотой 0.5 Гц. При вращении фонаря «зайчик» бежит по стене по горизонтальной прямой. Найдите скорость «зайчика» через 0.1 с после того, как луч света был перпендикулярен стене. 10. Скорость тела выражается формулой v=9–t2. Найти путь и перемещение тела через 10 секунд от начала движения. 11. Три точки находятся в вершинах равностороннего треугольника со стороной а. Они начинают одновременно двигаться с постоянной по модулю скоростью υ, причем первая точка все время держит курс на вторую, вторая - на третью, третья - на первую. Через сколько времени точки встретятся? 12. Зависимость координаты тела от времени дается уравнением x=9t–6t2+t3 (координата – в метрах, время – в секундах). Найти зависимость скорости и ускорения от времени; путь, перемещение, скорость и ускорение тела через 2 секунды после начала движения. Движение прямолинейное. 13. Зависимость координаты тела от времени дается уравнением x=16–9t2+2t3. Найти среднее значение модуля скорости и величину среднего ускорения тела в интервале времени от 1 секунды до 4 секунд. 14. Материальная точка движется прямолинейно. Уравнение движения тела имеет вид: x=2+3t+0.01t3 (координата – в метрах, время – в секундах). Каковы скорость и ускорение в моменты времени 0 с и 10 с от начала движения? 15. Первую половину времени своего движения автомобиль двигался со скоростью 40 км/ч, а вторую половину времени – со скоростью 80 км/ч. Определить среднюю скорость движения автомобиля. 16. Мотоциклист, имея начальную скорость 10 м/с, стал двигаться с ускорением 1 м/с2. За какое время он пройдет путь 192 м и какую скорость приобретет в конце пути? 17. Поезд, движущийся со скоростью 72 км/ч, проходит от начала торможения до остановки расстояние 1 км. Чему равно ускорение? Найти скорость поезда у светофора, находящегося в середине тормозного пути. 18. Тело, брошенное вертикально вверх, вернулось на землю через 3 с. Какова была начальная скорость тела? На какую высоту поднялось тело? 19. С балкона бросили мячик вертикально вверх с начальной скоростью 5 м/с. Через 2 секунды мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю. 20. С отвесной скалы падает камень. Через 6 секунд доносится звук удара о землю. Определить высоту скалы. Скорость звука 320 м/с. 21. Тело падает вертикально с высоты 19.6 м без начальной скорости. Какой путь пройдет тело за первую 0.1 с своего движения? За последнюю 0.1 с своего движения? 22. Тело падает вертикально с высоты 19.6 м без начальной скорости. За какое время тело пройдет первый метр своего пути? Последний метр своего пути? 23. Камень бросили вверх на высоту 10 м. Через сколько времени он упадет на землю? На какую высоту поднимется камень, если начальную скорость камня увеличить вдвое? 24. Тело падает без начальной скорости с высоты 490 м. Определить перемещение тела в последнюю секунду падения. 25. Камень, брошенный горизонтально с высоты 2 м над землей, упал на расстоянии 7 м от точки бросания (по горизонтали). Найти его первоначальную и конечную скорости. 26. Камень брошен горизонтально с высоты 30 м с начальной скоростью 30 м/с. На каком расстоянии по горизонтальному направлению и под каким углом к горизонту он упал? 27. Тело брошено горизонтально с высоты 20 м со скоростью 15 м/с. Через сколько времени тело упадет на землю? На каком расстоянии от места бросания по горизонтали упадет тело и какова будет его скорость в момент падения? 28. Тело, брошенное с башни в горизонтальном направлении, упало на расстоянии 40 м от основания башни под углом 450 к горизонту. Найти высоту башни и начальную скорость тела. 29. Тело, брошенное с башни в горизонтальном направлении со скоростью 20 м/с, упало на землю на расстоянии, вдвое большем, чем высота башни. Найти высоту башни. 30. Снаряд вылетел из дальнобойной пушки с начальной скоростью 1000 м/с под углом 300 к горизонту. Сколько времени снаряд будет находиться в воздухе? На каком расстоянии от пушки он упадет на землю? 31. Из одинаковых пожарных труб бьют струи воды: одна под углом 450 к горизонту, другая – 600. Во сколько раз наибольшая высота, достигаемая первой струей, меньше, чем вторая? 32. Мяч бросили со скоростью 10 м/с под углом 400 к горизонту. Найти: на какую высоту поднимется мяч; на каком расстоянии от места бросания мяч упадет на землю; сколько времени он будет в движении; под каким углом к горизонту летел мяч на половине максимальной высоты. 33. Тело брошено под углом к горизонту. Продолжительность полета 2.2 с. Найти наибольшую высоту подъема тела. 34. Пароход идет по реке от пункта А до пункта В со скоростью 10 км/ч, а обратно – 16 км/ч. Найти среднюю скорость парохода и скорость течения реки. 35. Наблюдатель, стоявший в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за 4 с. В течение какого времени мимо него будет двигаться n-й (7-й) вагон? Движение считать равноускоренным. 36. Тело брошено под углом 600 к горизонту со скоростью 20 м/с. Под каким углом к горизонту движется тело после начала движения через 1.5 с? Через 2.5 с? Через какое время и на какой высоте тело будет двигаться под углом 450 к горизонту?
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.22.169 (0.059 с.) |
 – уравнение неразрывности;
– уравнение неразрывности; – давление;
– давление; – гидростатическое давление;
– гидростатическое давление; – закон Архимеда;
– закон Архимеда; – уравнение Бернулли;
– уравнение Бернулли; – сила вязкого трения между слоями жидкости или газа;
– сила вязкого трения между слоями жидкости или газа; – кинематическая вязкость;
– кинематическая вязкость; – число Рейнольдса;
– число Рейнольдса; – закон Стокса;
– закон Стокса; – объемный расход;
– объемный расход; – формула Пуазейля.
– формула Пуазейля. – средняя скорость;
– средняя скорость; – средняя скорость вдоль траектории;
– средняя скорость вдоль траектории; – мгновенная скорость;
– мгновенная скорость; – величина мгновенной скорости;
– величина мгновенной скорости; – проекция скорости на ось OX;
– проекция скорости на ось OX; – среднее ускорение;
– среднее ускорение; – мгновенное ускорение;
– мгновенное ускорение;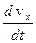 – проекция ускорения на ось OX;
– проекция ускорения на ось OX; – закон сложения скоростей.
– закон сложения скоростей. =const):
=const): – радиус-вектор материальной точки;
– радиус-вектор материальной точки; ;
;  ;
;  – длина пути;
– длина пути; – скорость при равнопеременном движении.
– скорость при равнопеременном движении.


