
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение расходящейся сферической волныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
r – расстояние от центра волны до т.М. Для гармонической сферической волны
где A (r) – амплитуда волны; φо – начальная фаза колебаний вцентре волны. Реальные источники волн можно считать точечными (источниками сферических волн), если расстояние r от источника колебаний до рассматриваемых точек среды значительно больше размера источника. Если r очень велико, то любые малые участки волновых поверхностей можно считать плоскими.
В однородной, изотропной, непоглощающей среде волны плоские и сферические описываются дифференциальным уравнением в частных производных, которое называется волновым уравнением, и имеет вид
Энергия волны
Упругая среда, в которой распространяются механические волны, обладает как кинетической энергией колебательного движения частиц, так и потенциальной энергией, обусловленной деформацией. Выбрав малый объём среды dV можно записать для плотности энергии
Для продольной плоской волны
Для плоскойгармонической волны
Для сферической гармонической волны
Среднее за период значение плотности энергии
Скорость переноса энергии равна фазовой скорости υ.
Потоком энергии
Так как
т.е. поток энергии через произвольную поверхность S, мысленно проведённую в среде, охваченной волновым движением, равен потоку вектора Умова через эту поверхность. Скалярная величина I, равная модулю среднего значения вектора Умова, называется интенсивностью волны:
Принцип суперпозиции волн: результирующее возмущение в какой либо точке линейной среды при одновременном распространении в ней нескольких волн равно сумме возмущений, соответствующей каждой из этих волн в отдельности.
Интерференция волн Две волны называются когерентными, если разность их фаз не зависит от времени. Гармонические упругие волны, частоты которых одинаковы, когерентны всегда. Рассмотрим наложение двух гармонических волн, возбуждаемых в однородной и изотропной среде точечными источниками S1 и S2, с циклическими частотами ω 1 = ω 2 = ω и начальными фазами φ 1и φ 2..
По принципу суперпозиции
А и Ф определяем по методу векторных диаграмм
Амплитуда результирующих колебаний максимальна
Амплитуда результирующих колебаний минимальна
Число т называют порядком интерференционного максимума.
Частным случаем интерференции волн являются стоячие волны, которые образуются в результате наложения двух бегущих синусоидальных волн, распространяющихся навстречу друг другу и имеющих одинаковые частоты и амплитуды, а в случае поперечных волн ещё и одинаковую поляризацию.
Тогда
Амплитуда стоячей волны Точки, в которых А СТ = 0 называются узлами стоячей волны, а точки, где А СТ = 2 А называются пучностями стоячкй волны. Положение узлов и пучностей находится из условий
Длиной стоячей волны называют расстояние между двумя соседними узлами или двумя соседними пучностями
В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), т.к. аргумент синуса в уравнении стоячей волны не зависит от координаты х. В стоячей волне скорость колебательного движения частиц среды
а относительная деформация среды
Таким образом, в отличие от бегущей волны, в стоячей волне В пучностях стоячей волны располагаются пучности скорости частиц и узлы деформации среды. Если l – длина струны, стержня или столба газа, υ – фазовая скорость волны, а λ – её длина, то для струн или стержней, закреплённых на обоих концах, и столбов газа в трубах, закрытых или открытых с обоих концов, на длине l укладывается целое число длин стоячей волны λСТ = λ /2. Отсюда вытекает условие
Для стержней, один конец которых закреплён, а другой свободен, и для труб, закрытых с одного конца и открытых с другого,
Лекция 8
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 915; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |

 , где
, где и
и  ,
, , где
, где – оператор Лапласа или Лапласиан.
– оператор Лапласа или Лапласиан.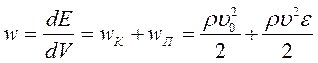 , где
, где – скорость колебаний частиц в среде;
– скорость колебаний частиц в среде; – фазовая скорость волны;
– фазовая скорость волны; – плотность среды;
– плотность среды; – относительная деформация.
– относительная деформация. и
и  , т.е.
, т.е. .
.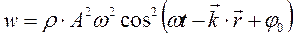 .
. .
.
 .
. через малую площадку
через малую площадку 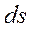 называется отношение
называется отношение  .
.
 , то
, то , где
, где – вектор плотности потока энергии или вектор Умова.
– вектор плотности потока энергии или вектор Умова.

 .
.


 .
. .
. – геометрическая разность хода волн от С1 и С2 до точки М.
– геометрическая разность хода волн от С1 и С2 до точки М. если
если  или
или . Если
. Если  то.
то. если
если 
 т.е.
т.е.  или
или . Если
. Если  .
.

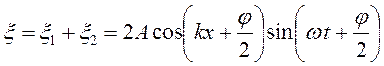 .
.
 является периодической функцией от координаты х.
является периодической функцией от координаты х. – узлы;
– узлы;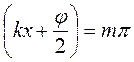 – пучности (т = 0; 1; 2; …).
– пучности (т = 0; 1; 2; …). .
. ,
,
 опережает υ 0 по фазе на π/ 2, так что в те моменты времени, когда υ 0 достигает амплитудного значения,
опережает υ 0 по фазе на π/ 2, так что в те моменты времени, когда υ 0 достигает амплитудного значения, 
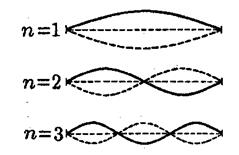
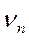 – собственные частоты колебаний таких систем (гармоники).
– собственные частоты колебаний таких систем (гармоники). – основной тон;
– основной тон; – первый обертон.
– первый обертон. .
.


