
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон ома для електричного кола змінного струмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо тепер електричне поле, яке містить резистор з активним опором R і малою індуктивністю, котушку з великою індуктивністю L і малим активним опором і конденсатор ємністю С (мал. 31). Нехай до кола приєднано джерело змінної напруги на амплітуда коливань сили струму з амплітудою коливань напруги, значеннями і?, L і С і частотою струму; від чого залежить і чому дорівнює зсув фаз між коливаннями сили струму в колі і коливаннями напруги, прикладеної до цього кола. Ми знаємо, що в колах постійного струму напруга на кінцях кола завжди дорівнює сумі напруг на окремих послідовно з'єднаних ділянках. Але якщо виміряти діючі значення напруг в усьому колі і на окремих ділянках кола (див. мал. 31), то виявиться, що діюча напруга в колі не дорівнює сумі напруг на окремих його ділянках. Це пояснюється тим, що гармонічні коливання напруги на різ- них ділянках кола зсунуті за фазою одне відносно одного. Дійсно, після встановлення режиму сила струму однакова на всіх ділянках кола. Це означає, що однакові амплітуди і фази струмів, які проходять ділянками з ємнісним, індуктивним, активним опорами. Однак лише на активному опорі коливання напруги й сили струму збігаються за фазою. На індуктивному опорі коливання напруги випереджають коливання сили струму на малюнку 32, а приведені графіки цих коливань для цілком певних значень знаходяться у протифазь Для будь-якого моменту часу сума миттєвих спадів напруг на Я, L і С завжди дорівнює напрузі, прикладеній до кола від генератора в цей момент часу: (20.1)
Тому графік напруги и відносно графіка сили струму можна дістати додаванням коливань На малюнку для порівняння показано і графік сили струму. З графіка випливає, що між коливаннями сили струму і напруги є певний зсув фаз. У даному випадку коливання напруги випереджають коливання сили струму. Неважко помітити, що коли змінити якийсь з елементів кола Я, L або С, то зміниться і зсув фаз між силою струму і напругою. Якщо коливання напруги и мають вигляд
де (р — зсув фаз між напругою и і силою струму і в колі.
Для коливань спадів напруг на активному опорі R, індуктивності L і ємності С маємо:
Підставивши замість (20.1), дістанемо
(20.2) Враховуючи, що
і виконавши тригонометричні перетворення, рівняння (20.2) можна переписати у вигляді: Одержане рівняння (20.4) повинно виконуватися в будь-який момент часу, а значить і для моментів часу, коли (20.4) дістанемо два рівняння:
(20.5) З цієї системи рівнянь можна визначити гого рівняння
(20.6) Таким чином, різниця фаз <р між силою струму і напругою
Якщо відомо
Величину опором кола. Від амплітуд сили струму й напруги можна перейти до діючих значень цих величин. Вони зв'язані такою самою залежністю, як і амплітудні значення:
Це і є закон Ома для кола змінного струму, яке містить послідовно увімкнуті резистор, котушку індуктивності і конденсатор. Із закону Ома (20.7) і виразу для зсуву фаз (20.6) можна дістати, як часткові випадки, всі співвідношення для розглянутих нами кіл. Пропонуємо самостійно переконатися в цьому. Вправа З 1. В коло змінного струму з частотою v = 400 Гц увімкнуті по 2. В коло змінного струму з напругою U— 220 В увімкнено послі § 21. Потужність в колі змінного струму Потужність в колі постійного струму обчислюється у всіх випадках за формулою Р= IU. За цією формулою можна обчислювати також потужність змінного струму (див. § 16), якщо під І та U розуміти діючі значення сили струму й напруги і якщо сила струму й напруга збігаються за фазою. Розглянемо, як обчислюється потужність змінного струму в загальному випадку. Нехай напруга в колі змінюється гармонічно за законом меться гармонічно з тією самою частотою, але у загальному випадку буде зсунута за фазою відносно напруги на кут
Для миттєвої потужності можна записати:
Миттєва потужність змінюється з часом як за модулем, так і за знаком (мал. 33). Протягом однієї частини періоду енергія надходить до даної ділянки кола (р>0), але за другу частину періоду певна кількість енергії знову повертається в коло (р<0). Як правило, у всіх випадках треба знайти середню потужність на ділянці кола за досить великий інтервал часу, який містить багато періодів. Оскільки сила струму й напруга мають постійні амплітуди і змінюються однаково, то середнє значення потужності за один період і за будь-яку кількість періодів буде однаковим. Тому
ft середня потужність в колі буде постійною. Отже, для знаходження потужності змінного струму достатньо знайти середню потужність за один період. Щоб знайти середню потужність за період, перетворимо спочатку формулу (21.1) так, щоб виділити в ній член, який не залежить від часу. З цією метою скористаємося відомою формулою для добутку двох синусів:
У даному випадку
Членне залежить від часу. На малюнку 34 він показаний кожної чверті періоду ця функція пробігає ряд додатних значень, а протягом наступної чверті періоду пробігає такий самий ряд від'ємних значень. Тому середня потужність за період дорівнює першому члену, який не залежить від часу:
Перейшовши від амплітудних значень сили струму й напруги до діючих, дістанемо:
j Цю величину називають просто потужністю змінноп струму на ділянці кола і позначають через Р:
Таким чином, потужність змінного струму на ділянці кола визначається діючими значеннями сили струму й напруги. Вона залежить також від зсуву фаз називається коефіцієнтом потужності, який показує, що електричне коло споживає від генератора не всю потужність, яку він може розвивати в даних умовах, а лише частину її. Друга частина циркулює між електричним колом і генератором. В одну частину періоду вона споживається колом, в другу — повертається з кола в генератор. Чим більший тина потужності від можливої споживається електричним колом, і навпаки, при малому cos ц (великі і електричне коло не споживає потужності Як же може виявитися той факт, що середня потужність дорівнює нулю при наявності струму в колі? Це пояснюють приведені на малюнку 35 графіки зміни з часом напруги, сили струму і миттєвої потужності при індуктивний опір ділянки кола). Графік залежності миттєвої потужності від часу можна дістати, перемножуючи значення сили струму й напруги в кожний момент часу.
З цього графіка видно, що протягом однієї чверті періоду потужність додатна і енергія надходить до даної ділянки кола; однак протягом наступної чверті періоду потужність від'ємна, і дана ділянка віддає без втрат назад в генератор одержану раніше енергію. Енергія, яка протягом чверті періоду надходила, нагромаджувалася в магнітному полі струму, а потім без втрат поверталась до генератора. Так буде, зокрема, якщо ділянка кола містить одну лише індуктивність чи ємність.
Лише при наявності активного опору в колі, яке не містить рухомих провідників, електромагнітна енергія перетворюється у внутрішню енергію провідників, нагріваючи його. Зворотного перетворення внутрішньої енергії в електромагнітну на активному опорі не відбувається. На практиці завжди прагнуть, щоб від генератора споживалась якомога більша частина вироблюваної ним потужності, тобто щоб соз ф був близьким до одиниці (ф має наближатися до нуля). Як цього можна добитися? Основний спосіб — повне завантаження приєднаних до генератора трансформаторів і двигунів. Припустимо, що на верстаті встановлено електродвигун потужністю 20 кВт. Під час нормальної роботи верстата двигун завантажено повністю і майже вся підведена до нього електрична енергія перетворюється в механічну. Коефіцієнт потужності в цьому випадку становить 0,90—0,95. Але якщо після закінчення обробки деталі робітник не вимкне електродвигун, то він працюватиме вхолосту, його cos (f знизиться до ОД—0,2 і двигун по суті становитиме індуктивне навантаження. Тому не можна залишати увімкненими електродвигуни, які працюють вхолосту. Не можна також і недовантажувати двигуни. Якщо, наприклад, для роботи верстата потрібен електродвигун потужністю 1 кВт, а на ньому встановили двигун потужністю 10 кВт, то він працюватиме майже вхолосту і його сов ф буде незначним. Електродвигун завжди треба добирати такої потужності, яка потрібна для приведення в дію робочої машини. Залежність потужності від cos <p завжди враховується при проектуванні ліній електропередачі на змінному струмові. Якщо cos ф лінії буде малий, то значна частина енергії циркулюватиме проводами від генератора до споживачів і назад. Оскільки проводи мають активний опір, то при цьому енергія витрачатиметься на їх нагрівання. Підрахуємо потужність цих втрат. До споживача звичайно подається напруга певного значення U, тому одна й та сама потужність Р споживатиметься при різних значеннях сили струму в колі / залежно від значення зсуву фази між силою струму і напругою. При малих значеннях cos ф сила струму має бути великою, що веде до великих теплових втрат в підвідних проводах лінії передачі. Якщо г — опір лінії передачі, то втрата потужності на нагрівання проводів лінії передачі Р\ дорівнює Таким чином,
Для промислових підприємств не допускається використання установок з коефіцієнтом потужності, меншим 0,85. § 22. Електричний резонанс. Резонанс напруг і струмів Оскільки змінний електричний струм є вимушеними електричними коливаннями, тому природно припустити, що в електричному колі змінного струму можливий резонанс. Амплітуда сили струму при вимушених коливаннях в контурі під дією зовнішньої гармонічно змінної напруги визначається, як відомо, формулою
Проаналізуємо цю формулу. При заданій напрузі Um і значеннях R, L і С сила струму залежить від частоти коливань а ємнісний — нескінченно великий і сила струму в колі дорівнює нулю. Сила струму в колі дорівнює нулю і при нескінченно великій частоті ( випадку при малих і великих частотах. Очевидно, максимальне значення сили струму буде при такій частоті соо, при якій знаменник у формулі матиме найменше значення. Це буде тоді, коли вираз у дужках під коренем стане рівним нулю, тобто
(22.1) При виконанні умови (22 1), тобто коли індуктивний опір котушки дорівнює ємнісному опору конденсатора і по колу йде однакова сила струму, однаковими будуть і амплітуди коливань напруги на конденсаторі та котушці. Коливання напруги на котушці і конденсаторі протилежні за фазою, тому сума напруг на них при виконанні умови (22.1) в будь-який момент часу дорівнює нулю. В результаті напруга на активному опорі під час резонансу буде дорівнювати повній напрузі:
Оскільки активний опір R електричних кіл звичайно малий, то під час резонансу сила струму може бути дуже великою. Із формули (22.1) можна визначити частоту (22.2)
Ця частота збігається з власною частотою вільних коливань у контурі з малим активним опором (див. формулу 10.5). Отже, явище електричного резонансу полягає в різкому зростанні амплітуди вимушених коливань сили струму в контурі з малим активним опором, коли збігаються частоти зовнішньої змінної напруги з власною частотою коливань контуру. У випадку механічних коливань резонанс проявляється тим чіткіше, чим менші втрати енергії в системі (чим менше тертя). Аналогічно до цього електричний резонанс проявляється тим сильніше, чим менше R, тобто чим менші енергетичні втрати в колі. Якщо й->-0, резонансне значення амплітуди сили струму необмежено зростає: /рез—>-оо. Навпаки, зі збільшенням R максимальне значення амплітуди сили струму зменшується. І коли R дуже великий, резонанс взагалі не виникає, аналогічно до того, як при великому терті не виникає резонанс в механічній системі. Залежність амплітуди сили струму від частоти при різних активних опорах R показана на малюнку 36, де
Під час резонансу амплітуда напруги на котушці індуктивності UL дорівнює амплітуді напруги на конденсаторі Uc. Значення цієї напруги можна знайти як добуток амплітуди сили струму під час резонансу на індуктивний або ємнісний опір:
Але тоді
(22.3) З рівняння (22.3) випливає, що амплітуда напруги на котушці індуктивності і конденсаторі під час резонансу в до кола. Якщо активний опір і ємність кола дуже малі, то скласти) дістанемо що в момент резонансу напруга на конденсаторі і котушці індуктивності може в сотні разів перевищити напругу, прикладену до кола. Це явище аналогічне до виникнення великих навантажень на окремі частини механічної системи під час резонансу. Як під час механічного резонансу можливе руйнування системи, так і під час електричного можливе руйнування електричного кола, наприклад, електричний пробій конденсатора, перегрівання провідників і пробій ізоляції. Під час резонансу, як це випливає з рівняння (20.6), зсув фаз між коливаннями сили струму і напруги дорівнює нулю. Дійсно, оскільки Це легко пояснити. Коливання напруги на котушці індуктивності і конденсаторі завжди відбуваються у протифазі і амплітуди цих напруг однакові. В результаті напруги на котушці і конденсаторі повністю компенсують одна одну ному опорі. А на активному опорі фази коливань сили струму і напруги збігаються. Явище резонансу в електричному колі можна спостерігати на такому досліді. До електричного кола (мал. 37) з послідовно увімкнутих резистора, котушки індуктивності, конденсатора і амперметра змінного струму приєднують генератор змінної напруги регульованої частоти, наприклад генератор звукової частоти. Паралельно до конденсатора чи котушки індуктивності вмикають вольтметр змінного струму. Збільшуючи поступово частоту коливань генератора, можна спостерігати, що сила струму в колі і напруга на конденсаторі (чи котушці індуктивності) спочатку дуже повільно, а потім все швидше зростають. При резонансній частоті вони зростають в десятки і навіть сотні разів. Якщо далі збільшувати частоту, сила струму і напруга починають спочатку швидко, а потім все повільніше зменшуватися і при досить великій частоті майже дорівнюють нулю. Електричний резонанс в колі можна одержати не тільки зміною частоти генератора, а й при заданій частоті, змінюючи або індуктивність котушки, або ємність конденсатора. Досі ми розглядали кола змінного струму, в яких резистор, конденсатор і котушка з'єднані послідовно. Розглянемо тепер коло з увімкнутими паралельно котушкою і конденсатором (мал. 38). Припустимо, що активний опір обох віток розгалуження настільки малий, що ним можна нехтувати. До клем кола а і b прикладена змінна синусоїдальна напруга Напруга на паралельно з'єднаних вітках розгалуження однакова і дорівнює прикладеній напрузі
Оскільки сила струму у вітці розгалуження, яка містить конденсатор, випереджає напругу на
кола має вигляд, показаний на малюнку 39. Векторна діаграма дає можливість записати вирази для миттєвих значень сили струму в обох вітках розгалуження: Коли ємнісний і індуктивний опори однакові, тобто
то сила струму в нерозгалуженій частині кола дорівнює нулю, хоча в контурі, який складається з L і С, сила струму може бути дуже великою. Це явище називається резонансом струмів. Для резонансної частоти з рівності (22.2) дістанемо таке саме значення, що й при резонансі напруг. Для струму резонансної частотиконтур з малим активним опором R становить дуже Резонанс струмів (резонанс напруг) широко використовується в техніці. Для прикладу розглянемо будову і принцип дії найпростішого резонансного підсилювача (мал. 40). В анодне коло підсилювача вмикають коливальний контур, настроєний на частоту сигналу, який треба підсилити. Для резонансної частоти (точніше, для вузької смуги частот) контур становить великий опір і коливання анод-
ного струму лампи викликають на його кінцях появу змінної напруги. Для цієї частоти резонансний підсилювач діє так само, як і звичайний підсилювач на резисторах, причому роль анодного опору відіграє коливальний контур. Для всіх інших частот, які помітно відрізняються від резонансної, контур є практично коротким замиканням анодного кола, і тому підсилення напруги не відбувається. Ви вже знаєте, що під час резонансу струмів силу струму в обох вітках розгалуження кола можна зробити набагато більшою, ніж у підвідних проводах. Цю обставину використовують в індукційних печах, в яких нагрівання металів здійснюється вихровими струмами. Для цього паралельно нагрівальній котушці К вмикають конденсатор С і добирають його ємність так, щоб одержати на частоті генератора, який живить піч, резонанс струмів. Тоді через підвідні проводи і генератор проходить порівняно невеликий струм, сила якого дорівнює різниці Ік — Іс і яку можна зробити в десятки разів меншою, ніж силу струму Ік в нагрівальній котушці. З викладеного вище випливає, що електричний резонанс в колі можливий лише в тому випадку, коли воно містить одночасно і ємність, і індуктивність. В колах, які містять лише ємності, або лише індуктивності, резонанс не спостерігається. Явище резонансу в електричних колах відіграє дуже велику роль в електротехніці і радіотехніці. З деякими важливими галузями його застосування ми далі ознайомимося. ? 1. У чому суть електричного резонансу? 2. Чому дорівнює амплітуда сили струму під час резонансу? 3. Від яких параметрів кола залежить резонансна частота контуру? 4. Чи може амплітуда напруги на конденсаторі чи котушці індуктивності під час резонансу перевищити амплітуду напруги, прикладеної до кола? 5. Чи існує зсув фаз між коливаннями сили струму і напруги під час резонансу? Чому? в. Чи може спостерігатися резонанс у колі, яке містить лише активний і ємнісний, або активний та індуктивний опори?
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 981; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.250.115 (0.011 с.) |

 . З'ясуємо, як зв'яза-
. З'ясуємо, як зв'яза- , а на ємнісному — відстають на
, а на ємнісному — відстають на  . На
. На . Зверніть увагу, що графіки
. Зверніть увагу, що графіки 

 (мал. 32, б).
(мал. 32, б). то для коливань сили струму в загальному випадку можна записати:
то для коливань сили струму в загальному випадку можна записати:
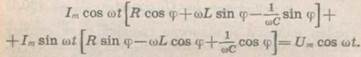

 їх значення у формулу
їх значення у формулу
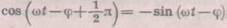 ;
;

 . Для цих моментів часу з рівняння
. Для цих моментів часу з рівняння
 . З дру-
. З дру-
 в колі залежить від частоти w і параметрів кола
в колі залежить від частоти w і параметрів кола

 , то
, то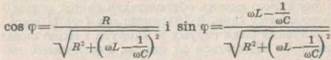
 називають повним
називають повним (20.7)
(20.7) . Тоді й сила струму змінювати-
. Тоді й сила струму змінювати- :
:
 або
або

 . Тому
. Тому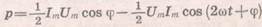
 прямою MN, паралельною абсцисі. Другий член є синусоїдальною функцією часу. Середнє за період значення
прямою MN, паралельною абсцисі. Другий член є синусоїдальною функцією часу. Середнє за період значення 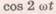 дорівнює нулю, оскільки протягом
дорівнює нулю, оскільки протягом


 (21.2)
(21.2) між напругою і силою струму. Множник
між напругою і силою струму. Множник  у формулі (21.2)
у формулі (21.2) (чим менший),
(чим менший),  тим більша час-
тим більша час- ) від генератора споживається менша частина потужності від тієї, яку він може виробляти. Зокрема, якщо
) від генератора споживається менша частина потужності від тієї, яку він може виробляти. Зокрема, якщо при будь-яких значеннях U і 7, навіть якщо вони максимальні для даного генератора. Генератор працює вхолосту.
при будь-яких значеннях U і 7, навіть якщо вони максимальні для даного генератора. Генератор працює вхолосту. (чисто
(чисто
 . Сила струму в проводах. Тоді
. Сила струму в проводах. Тоді якщо навантаження
якщо навантаження  споживача постійкєіг зменшення cos ф веде не лише до неповного використання потужності генератора, а й до збільшення теплових втрат в колі.
споживача постійкєіг зменшення cos ф веде не лише до неповного використання потужності генератора, а й до збільшення теплових втрат в колі.
 . При
. При  індуктивний опір дорівнює нулю,
індуктивний опір дорівнює нулю, ), оскільки в цьому
), оскільки в цьому . Сила струму буде незначною
. Сила струму буде незначною
 . Це означає, що сила струму в колі визначається лише активним опором R, дії індуктивності і ємності взаємно компенсуються. Це явище називається резонансом напруг. Сила струму в колі досягає максимального значення
. Це означає, що сила струму в колі визначається лише активним опором R, дії індуктивності і ємності взаємно компенсуються. Це явище називається резонансом напруг. Сила струму в колі досягає максимального значення
 , при якій настає резонанс (резонансну частоту):
, при якій настає резонанс (резонансну частоту):




 разів більша за амплітуду напруги, прикладеної
разів більша за амплітуду напруги, прикладеної може значно перевищити одиницю. Наприклад, для
може значно перевищити одиницю. Наприклад, для  (таке коло легко
(таке коло легко . Цей приклад показує,
. Цей приклад показує, , то
, то  і
і 
 і спад напруги відбувається лише на актив-
і спад напруги відбувається лише на актив- . Треба визначити коливання сили повного струму в колі (тобто сили струму, яку вимірює амперметр А, увімкнутий до підвідних провідників).
. Треба визначити коливання сили повного струму в колі (тобто сили струму, яку вимірює амперметр А, увімкнутий до підвідних провідників). . Миттєве значення сили струму в нерозгалуженій частині кола /(*) дорівнює алгебраїчній сумі сил струмів в паралельних вітках розгалуження;
. Миттєве значення сили струму в нерозгалуженій частині кола /(*) дорівнює алгебраїчній сумі сил струмів в паралельних вітках розгалуження; 


 , а сила струму через котушку відстає від напруги на -г-л, то векторна діаграма для цього
, а сила струму через котушку відстає від напруги на -г-л, то векторна діаграма для цього

 (22.2)
(22.2) великий опір, тим більший, чим менше R (при
великий опір, тим більший, чим менше R (при  опір контуру Z прагне до нескінченності).
опір контуру Z прагне до нескінченності).



