
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наростання і спад струму в колі з індуктивністю.Содержание книги
Поиск на нашем сайте
Енергія магнітного поля Спадання струму в колі з індуктивністю:
Fig 72 Якщо включити ключ в положення 1,то в колі протікатиме струм І0: Якщо ключ перевести в положення 2 (розірвати коло), записавши 2-ге правило Кірхгофа отримаємо: Використавши початкові умови, одержимо t=0, I=I0 (в момент вимкнення); t=0,
Fig 73 Наростання струму в колі з індуктивнівстю: Вмикаємо коло, і при t=0, I=0. Використовуючи друге правило Кірхгофа запишемо наступне рівняння:
Fig 74 Енергія магнітного поля: При наростанні струму в контурі повинна виконуватись якась робота проти
Основні положення теорії електромагнітного Поля Максвелла Максвелл створив єдину теорію електромагнітного поля, він об’єднав всі відомі дані в сім рівнянь Максвелла, які дозволяють описати явище, що входить в рамки класичної електродинаміки. Він зробив два припущення на основі яких одержано два нові рівняння. В цілому теорія Максвелла стверджує, що електричне і магнітне поле є частковим випадком єдиного електромагнітного поля. 1-ше припущення (про існування вихрового електричного поля):Поряд з безвихровим електростатичним полем може існувати вихрове електричне поле. Електричне поле, яке виникає підчас явища електромагнітної індукції є вихровим. Приклад: Масивний металевий диск поміщений в змінне магнітне поле, в даному провідникові виникають вихрові струми Фуко. Ці струми є замкнуті, зовнішнього джерела струму тут немає, а це означає, що струм існує за рахунок вихрового електричного поля.
Fig 75 Масивний металевий диск в змінному магнітному полі
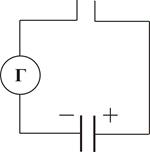
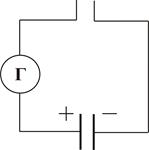
а) б) На практиці переважно використовують перший фактор. 2 припущення: В природі всі електричні струми замкнуті: струми провідності в провідниках замикаються струмами зміщення в діелектриках. Появу магнітного поля можуть викликати не лише струми провідності, але й змінне електричне поле, яке називають струмом зміщення. Щоб ввести кількісне порівняння між струмом провідності і струмом зміщення проведемо дослід. Розглянемо схему на рисунку. Перемикач періодично перемикаємо в верхнє і нижнє положення.
Fig 76
Fig 77-78 У нижньому положенні: При вмиканні гальванометр покаже імпульс струму, що виникає при зарядці конденсатора. Конденсатор набуває заряду У верхньому положенні: При вмиканні у верхнє положення відбувається зміна знаку заряду конденсатора, гальванометр фіксує імпульс струму. Якщо періодично перемикати, то в колі гальванометра тектиме струм змінного напрямку 1. 2. 3. 4. 6. 7. Ця сукупність семи рівнянь називається рівняннями Максвелла. Крім того, до них відносять рівняння неперервності (виводиться з рівняння Подіємо на дане рівняння оператором дівергенції (скалярно помножимо на оператор Набла): Електричне і магнітне поле це частинні випадки електромагнітного поля. Максвелл показав, що воно єдине. Електричне і магнітне поле можуть виникати за рахунок взаємних перетворень: Магнітне поле в речовині Середовище впливає на магнітну взаємодію: індукція магнітного поля в середовищі в μ раз більша за індукцію поля в вакуумі; 1) 2) 3) Є ще четвертий клас Різні властивості цих речовин є результатом різної будови. Перший, хто висловив гіпотезу про природу відклику речовин на магнітне поле був Ампер, який висловив так звану гіпотезу про молекулярні струми. Суть гіпотези: В речовині існують молекулярні струми. Кожен струм є замкнутий і має свій магнітний момент При внесенні речовини в магнітне поле магнітні моменти цих струмів якимось чином орієнтуються, і в результаті виникає магнітне поле, яке накладається на зовнішнє поле, тому Виходячи з цієї гіпотези можна розпочати пояснення магнітних властивостей речовин
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.235.66 (0.009 с.) |


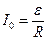 .
. .
. lnI=lnI0
lnI=lnI0  . Або
. Або  ; де
; де  - постійна часу; і якщо
- постійна часу; і якщо  ,то ми отримаємо в
,то ми отримаємо в 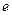 раз менший струм.
раз менший струм.

 . Тоді
. Тоді  , де
, де  - частковий розв’язок неоднорідного рівняння. Вводиться з наступних умов: при
- частковий розв’язок неоднорідного рівняння. Вводиться з наступних умов: при 
 , а
, а  ; при
; при  ,
,  . Тоді
. Тоді  .
.
 , в результаті цього струм набуває свого максимального значення поступово, і навпаки, після вимикання струму, струм в колі теж зникає поступово. Протікання цього струму підтримується за рахунок дії
, в результаті цього струм набуває свого максимального значення поступово, і навпаки, після вимикання струму, струм в колі теж зникає поступово. Протікання цього струму підтримується за рахунок дії  , при протіканні через нього струму
, при протіканні через нього струму  , існує певний запас енергії, який набувається під час наростання струму і втрачається при вимиканні кола. Величину цієї енергії знайдемо як роботу проти
, існує певний запас енергії, який набувається під час наростання струму і втрачається при вимиканні кола. Величину цієї енергії знайдемо як роботу проти  (знак мінус, оскільки робота виконується проти
(знак мінус, оскільки робота виконується проти 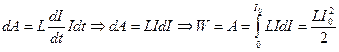 . Якщо говорити більш загально, то
. Якщо говорити більш загально, то 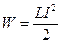 . Запишемо вираз для індуктивності соленоїда:
. Запишемо вираз для індуктивності соленоїда:  . Підставивши його у попереднє рівняння отримаємо енергію магнітного поля соленоїда:
. Підставивши його у попереднє рівняння отримаємо енергію магнітного поля соленоїда: 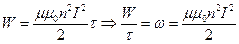 , де
, де  - енергія, що припадає на одиницю об’єму. Якщо розглядати просторову залежність густини енергії, то
- енергія, що припадає на одиницю об’єму. Якщо розглядати просторову залежність густини енергії, то  .В загальному випадку густина енергії магнітного поля
.В загальному випадку густина енергії магнітного поля 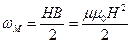 , а густина енергії електричного поля
, а густина енергії електричного поля  . Як бачимо вирази дуже подібні між собою.
. Як бачимо вирази дуже подібні між собою. , аМаксвелл стверджував, що
, аМаксвелл стверджував, що  .
. .
.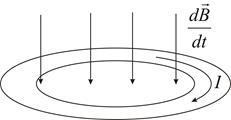
 передбачає зміну потоку за рахунок двох факторів:
передбачає зміну потоку за рахунок двох факторів: - залежність магнітної індукції від часу;
- залежність магнітної індукції від часу; - можливість зміни потоку за рахунок зміни геометрії контура.
- можливість зміни потоку за рахунок зміни геометрії контура. . Використовуючи теорему Стокса представимо дану рівність наступним чином:
. Використовуючи теорему Стокса представимо дану рівність наступним чином:  - перше рівняння Максвелла в диференціальній формі. В електростатичному полі
- перше рівняння Максвелла в диференціальній формі. В електростатичному полі  , і згідно з принципом суперпозиції
, і згідно з принципом суперпозиції  . Отже
. Отже  , або
, або  .
.
 .
.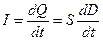 , бо
, бо  . Зауважимо, що в плоскому конденсаторі
. Зауважимо, що в плоскому конденсаторі  . Введемо величину
. Введемо величину  - густина струму зміщення. Дослідно було відкрито, що у випадку наявності змінного електричного поля у просторі виникає магнітне поле. Виходячи з цього Максвелл сформулював такі вирази:
- густина струму зміщення. Дослідно було відкрито, що у випадку наявності змінного електричного поля у просторі виникає магнітне поле. Виходячи з цього Максвелл сформулював такі вирази:  ,
, 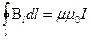 . Дане рівняння Максвелла можна записати таким чином:
. Дане рівняння Максвелла можна записати таким чином:  , або
, або 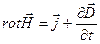 - друге рівняння Максвелла в диференціальній формі.
- друге рівняння Максвелла в диференціальній формі. ,
,  ,
, 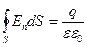 ,
,  ,
, 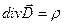 ;
; ,
,  ;
; ;
; ;
; .
.

 - рівняння неперервності. Воно стверджує, що зміна об’ємної густини заряду можлива лише за рахунок внесення чи виносу з об’єму заряду електричними струмами.
- рівняння неперервності. Воно стверджує, що зміна об’ємної густини заряду можлива лише за рахунок внесення чи виносу з об’єму заряду електричними струмами. , і
, і  . Цим ми підкреслюємо, що це вихрові поля.
. Цим ми підкреслюємо, що це вихрові поля.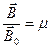 (відносна магнітна проникливість – безрозмірна величина). Є три категорії речовин:
(відносна магнітна проникливість – безрозмірна величина). Є три категорії речовин: (
( такі речовини називають діамагнетиками;
такі речовини називають діамагнетиками; (
( такі речовини називають парамагнетиками;
такі речовини називають парамагнетиками; (
( такі речовини називають феромагнетиками;
такі речовини називають феромагнетиками; (порядку одиниці) – антиферомагнетики.
(порядку одиниці) – антиферомагнетики. .
. .
.


