
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сили. Фундаментальні взаємодії в фізиці. Поняття про силові поля.Содержание книги
Поиск на нашем сайте
Сили. Фундаментальні взаємодії в фізиці. Поняття про силові поля.
В механіці розрізняють три основні типи сил: 1. Гравітаційна сила 2. Сили пружності 3. Сили тертя
Всю сукупність можливих в природі сил можна розбити на 4 основні класи, які називають фундаментальними взаємодіями. 1. Сильні взаємодії (ядерні) Якщо прийняти, що ядер. сили 1 Н 2. Електромагнітні взаємодії то 10-2 Н 3. Слабкі взаємодії 10-10 Н 4. Гравітаційні взаємодії 10-38 Н Ядерні взаємодії є близькодіючі сили (діють на відстані ~ 10-15м), тому вони відповідають за існування ядер та протікання ядерних реакцій. Елетро-магнітні взаємодії відповідають за існування атомів та молекул, на їх основі пояснюються хімічні реакції, радіус дії r, 0 < r < ∞. Слабкі взаємодії, типу ядерних, які виникають при взаємних перетвореннях елементарних частинок (радіуси дії r ~ 10-15 м). Гравітаційні взаємодії - найслабші (0 < r < ∞), однак сили, які ці взаємодії спричиняють є дуже великі за рахунок дії дуже великих мас. За яким законом відбувається та чи інша взаємодія? Для прикладу взаємодія двох точкових електричних зарядів описується законом Кулона (сила взаємодії між зарядами прямопропорційна добутку цих зарядів і оберненопропорційна квадрату відстані між ними): Була спроба пояснити, що заряди взаємодіють на відстані (принцип далекодії). Подібно намагалися пояснити гавітацію і т.д. Однак вияснили, що середовище якимось чином впливає на взаємодію. Елементарна суть такого принципу така: всяке джерело силової взаємодії створює довкола себе певний напружений стан середовища, яке ми називаємо силовим полем, відповідно об’єкти взаємодіють між собою через свої силові поля. Макроскопічні силові поля ми будемо характеризувати по наступних ознаках: яким чином проявляється сила, яким чином в цьому полі виконується робота і т.і. Відповідно до цих ознак силові поля поділяють на 3 основні типи: 1) Потенціальні (консервативні) силові поля:електростатичне, гравітаційне. Характерною рисою є те, що робота в них не залежить від вигляду траєкторії, а залежить лише від початкового і кінцевого положення.
А1,2 Fig 1 В цих полях робота по замкнутому контуру має бути рівна 0, тобто (якщо перейти до поверхневого інтеграла)
1) вихрові поля: Вихрове електричне поле, поле сторонніх сил має аналогічні властивості. 2) дисипативні силові поля - поля в яких йде розсіювання енергії, в математичному сенсі подібні до вихрового поля. Робота теж залежить від шляху. Прикладом такого типу полів є поля сил тертя. Під макроскопічним силовим полем розглядаємо певну ділянку простору, в кожній точці якого на внесене тіло діє якась сила.
Консервативні силові поля. Гравітаційне та електростатичне поле належать до консервативних силових полів, оскільки в них робота по замкненій ділянці траєкторії рівна нулеві.
В векторній формі: 1 2 В системі CI Поле створене точковими масами (чи зарядами) називається центрально-симетричним (F~ Покажемо, що воно є потенціальним.
Fig2 Переносимо заряд
Робота залежить лише від положення початкової і кінцевої точки і не залежить від вигляду траєкторії, тобто центрально-симетричне поле є потенціальним. Принцип суперпозиції полів. Якшо силове поле створене декількома джерелами, то напруженість сумарного поля в точці з координатою
Fig 3 Для електричних полів це також справедливо (тут слід враховувати знаки). Для суперпозиції потенціалів справедлива така сума:
Fig 4 Кожний силовий центр діє на кожну частинку не залежно від інших.
Електричне поле в речовині. Всі речовини умовно можна поділити на два класи: провідники і непровідники (діелектрики). Є ще напівпровідники. В провідниках (це як правило метали) є вільні заряди які можуть вільно переміщуватись всередині провідника. Носієм негативного заряду є електрони - Всяка речовина, яка перебуває в нормальному стані звичайно є нейтральна, тобто кількість електронів і протонів однакова. Якщо в зразку є негативний заряд, то в ньому надлишок електронів, якщо речовина заряджена позитивно, то в ній недостача електронів. Провідники мають таку хімічну будову, що валентні електрони атомів цих речовин зв’язані із своїми ядрами достатньо слабо, і тому практично вільно переміщаються в провіднику. В діелектрику всі валентні електрони приймають участь у створенні хімічних зв’язків, а тому локалізовані біля своїх атомів. Напівпровідники займають середнє положення між провідниками і діелектриками, тобто в цих речовинах мало вільних зарядів. В принципі, будь-яка речовина за певних умов може стати провідником.
Електрична ємність тіл.
Електрична ємність тіла позначається символом [ В системі СГС [ Приклади обчислення ємності деяких тіл. 1) Ємність сфери.
Fig 19
2) Ємність земної сфери.
Ємність окремих тіл є достатньо мала,але система електрично пов’язаних тіл має набагато більшу ємність. (до прикладу такою системою є так званий конденсатор).
3) Сферичний конденсатор:
Fig 20
4) Ємність плоского конденсатора:
Fig 21
Диполь в електричному полі. Диполем називають два заряди протилежних знаків, які електростатично взаємодіють між собою і знаходяться на певній відстані один відносно одного.
Fig 24 Властивості диполя характеризує величина Неоднорідне поле зорієнтує диполь вздовж силових ліній, а після цього буде втягувати диполь всередину поля. Молекули діелектрика можуть бути полярні і неполярні. Можливі випадки, коли молекули можуть ще до внесення в електричне поле являти собою диполі (наприклад NaCl). При внесенні в зовнішнє поле полярні молекули ведуть себе як жорсткий диполь; неполярні молекули при внесенні в зовнішнє поле, робляться пружнім диполем. Приклад неполярних молекул: молекули води, азоту, водню, кисню. При внесенні в поле діелектрика проходять наступні явища: поле орієнтує полярні молекули, цій орієнтації протидіє тепловий рух молекул, тому чим вища температура тим слабша орієнтація молекул. Поле перетворює в диполі молекули неполярного діелектрика.
Fig 25 Тобто на поверхні внесеного діелектрика виникають та звані зв’язані заряди з поверхневою густиною
Для розрахунку Під дією електричного поля речовина набуває якогось дипольного моменту , а по величині Тоді тут æ-електрична сприятливість, тобто
Властивість æ: 1) æ не залежить від температури для речовин, молекули яких неполярні. 2)æ
Fig 26
Сегнетоелектрики. Є ряд речовин, які мають дуже велике значення відносної діелектричної проникливості
Fig 27 1) Якщо поляризувати сегнетоелектрик, то виникає петля гістерезису представлена на рисунку 21. Тут
2) Для будь-якого сегнетоелектрика існує температура, вище якої він перетворюється в звичайний діелектрик (температура Кюрі). æ
Fig 28 3) Сегнетова сіль має дві точки Тк (дві температури Кюрі).
Дані властивості сегнетоелектрика можна пояснити наступним чином: ще до внесення в зовнішнє електричне поле, всередині діелектрика існують поляризовані ділянки. Ці ділянки, які називають доменами (з розмірами порядку 10-3см), поляризовані до насичення; і коли діелектрик вноситься в поле, то ділянки з протилежним напрямком поляризації зменшуються, а потім зникають і виникає така картина:
Fig 29 Існування температури Кюрі ( Крім сегнетової солі до сегнетоелектриків відносять кварц SiO2 та титанат барію BaTiO3.
Закони Кірхгофа В загальному випадку закони Кірхгофа – це узагальнення закону Ома. 1) Вираз закону збереження заряду: Алгебраїчна сума струмів у вузлі дорівнює нулю. Вузол – це точка де з’єднується не менше двох провідників.
Fig 36
2) Узагальнення закону Ома для повного кола.
Fig 37 В довільному замкнутому контурі взятому в межах кола алгебраїчна сума спадів напруг дорівнює сумі електрорушійних сил, що діють в цьому контурі Застосуємо правила Кірхгофа для схеми представленої на рисунку 9: Перший закон: Другий закон:
Правила Кірхгофа дозволяють розраховувати електричний струм і напругу в складних електричних колах.
Метали При температурі
Fig 38 Фізичний зміст коефіцієнта Якщо побудувати залежність питомого опору від температури, то при температурах нижчих за певну температуру Дебая (для кожного металу своя) опір металу еквівалентний
а б Fig 39-40 а) При б) При критичній температурі опір падає до нуля і маємо стан надпровідності. На сьогоднішній день вважається, що перенос заряду в металах здійснюється в основному електронами. На початку минулого століття Рікі поставив дослід: три циліндри з різних металів поставили в холод, щоб не було дифузії і протягом року пропускали струм. За цей час пройшов заряд
Fig 41-42 Було проставлено досліди по визначенню питомого заряду носіїв струму в металі і з них виявили, що носіями є електрони, вони практично можуть вільно переміщатись в металі. Їхній питомий заряд: Друде і Лоренц створили першу класичну теорію провідності металів.
Класична теорія провідності металів та її недоліки. Згідно з теорію Друде-Лоренца валентні електрони атомів металів відриваються від своїх атомів, стають спільними для всього зразка і можуть практично вільно переміщуватись в металі. Якщо прикласти зовнішнє поле напруженістю
де
Fig 43 Таким чином, густина струму в металі:
Час вільного пробігу
Відомо, що
Друде і Лоренц пояснили чому при протіканні струму виділяється тепло. Вважалось, що при зіткненні з граткою електрон повністю втрачає напрямлену складову швидкості, тобто при кожному ударі віддає таку порцію енергії гратці:
Тобто теорія Друде-Лоренца добре пояснила закон Джоуля – Ленца. Проте, незважаючи на всі переваги ця модель мала ряд неточностей: 1) Виявилось, що модель, використана в теорії Друде –Лоренца не знала як правильно пояснити температурну залежність опору металів: 2) Для того, щоб виходили розумні значення При такому густому розміщенні атомів для того, щоб пройти відстань 3) Теорія не зуміла пояснити так звану електронну теплоємність. 4) Теорія не могла припустити існування явища надпровідності. 5) З точки зору даної теорії не можна було пояснити властивості напівпровідників і діелектриків. Все це привело до потреби створення більш досконалої теорії, зокрема в 30-х р. минулого століття Зоммерфельд використав поняття електронних хвиль і з допомогою цього підходу розв’язав більшість проблем, пов’язаних з теорією металів. Зокрема пояснив температурну провідність металів, високе значення Напівпровідники До напівпровідників входить широкий клас речовин. Особливе практичне значення мають германій та кремній (Ge, Si), які стали основою розвитку твердотільної електроніки.
Fig 44 Провідність напівпровідників на декілька порядків нижча ніж провідність металів. Характерною рисою напівпровідників є те, що питомий опір напівпровідника з ростом температури нелінійно спадає. В більшості випадків питомий опір напівпровідників може бути виражений як:
Отже, є експоненціальна залежність питомого опору (питомої провідності) від температури. Якщо побудувати залежність
Fig 45 При низьких температурах всі валентні електрони атомів приймають участь у створенні хімічних зв’язків, в результаті чого в речовині відсутні вільні електрони, тобто немає носіїв струму; зокрема в Ge, який є чотирьох валентним, схему зв’язку малюють так:
Fig 46 Кожен атом взаємодіє з 4-ма сусідами, утворюючи ковалентні (міцні) зв’язки. При нагріванні речовини деякі зв’язки розриваються, тобто окремі електрони стають вільними. В результаті з’являються вільні електрони і електронні вакансії, які називають «дірками». Якщо до напівпровідника прикласти зовнішнє поле, то з’явиться напрямлений рух електронів до позитивного полюса батареї, а дірок – до негативного. Тобто, носіями струму в напівпровідниках є електрони і дірки, тому густина струму, що протікає через напівпровідник запишеться через наступне співвідношення: (обидва числа додатні, бо швидкості напрямлені в різні боки). Провідність, при якій концентрація електронів і дірок є одинакові Провідність напівпровідника може бути збільшена, якщо в нього ввести домішки. Атоми-домішки звичайно зв’язані з атомами напівпровідника іншим чином, ніж атоми напівпровідника між собою і ця відмінність може забезпечити домішкову провідність. Найкраще це видно при розгляді домішок іншої валентності. Нехай домішковий атом має п’ять валентних електронів. Якщо замінити атом Ge атомом домішки, то 4 валентні електрони домішкового атому приймають учать в створенні хімічних зв’язків, а 5-ий виявляється зайвим і при досить слабкому нагріванні може відірватись від свого атома (в атомі виникає вільний електрон без виникнення дірки). Дане явище проходить при нижчих температурах, ніж проявляється власна провідність напівпровідника. Тому при низьких температурах домішкова провідність відіграє визначальну роль. Такий тип домішок називається донором і викликає появу Величина Домішкова провідність, яка накладається на власну має свою експоненту з меншою енергією активації. Це можна виявити з аналізу температурної залежності провідності.
Fig 47
Провідність електролітів
Провідність електролітів здійснюється позитивними і негативними іонами, причому з підвищенням температури провідність зростає, тобто опір зменшується.
Fig 48 Провідність електролітів описується як
Є 2 причини за якими зростає 1) з ростом 2) з ростом Провідність газів Гази є діелектриками. Вольт-амперна характеристика газів виглядає наступним чином:
Fig 49-50 Протікання струму в газі називається газовим розрядом. Ділянка 0-2 відповідає «несамостійному» розряду. Ділянка 2-3 – самостійному. Носіями струму в газі є позитивні іони. На ділянці несамостійного розряду носії струму утворюються за рахунок дії зовнішніх іонізаторів (таких як сонячне сівтло, нагрів і т. д.). На ділянці 2-3 різке зростання струму обумовлене тим, що концентрація носіїв струму різко зростає за рахунок процесів, що протікають у газовому розряді. Нові носії струму виникають за рахунок таких процесів: 1) термоелектронна емісія з катода-при нагріванні катода з нього можливе випускання електронів; 2) вторинна електронна емісія-електрони випускаються катодом при бомбардуванні його іонами; 3) ударна іонізація - якщо напруженість поля в газі достатньо висока, то електрони можуть набувати енергії достатньої, щоб при зіткненні з молекулою газу іонізувати цю молекулу; 4) фотоіонізація - газовий розряд звичайно світиться і можлива іонізація молекул газу при поглинанні квантів цього світла; 5) автоіонізація - якщо напруженість поля в газі дуже висока, то можлива іонізація молекул газу під дією цього поля. Іонізований газ називають плазмою. Розрізняють такі 2 види плазми газового розряду: 1) низькотемпературна плазма - від ядер відриваються лише валентні електрони. (звичайна плазма) 2) високотемпературна плазма - при якій всі електрони відірвані від своїх ядер. (термоядерна плазма) В першому випадку енергія електронів відповідає температурі T~(20-30)*103 K (оскільки Для високотемпературної плазми T~107 К. Обидва види плазми наявні зорям (зокрема Сонцю), водневій бомбі. У плазмі можливі так звані ядерні реакції синтезу. Основними серед самостійних газових розрядів є: 1) тліючий розряд – тип газового розряду із неоднорідним розподілом електричного поля між катодом і анодом.Це самостійний розряд, в якому катод випромінює електрони внаслідок бомбардування позитивними йонами й високоенергетичними світловими квантами.Його використовують в неонових лампах; 2) дуговий – вид самостійного газового розряду, який виникає за високої температури між електродами, розведеними на невелику відстань і супроводжується яскравим світінням у формі дуги. Прикладом є електрозварка (при розведенні електродів виникає дуга). Для дуги характерна падаюча вольт амперна характеристика;
Fig 51 3) іскровий – має вигляд яскравих зигзагоподібних розгалужених ниток — каналів іонізованого газу, які пронизують розрядний проміжок і зникають, замінюючись новими. Супроводжується виділенням великої кількості теплоти і яскравим свіченням газу. Явища, які характеризують даний розряд, викликаються електронними та іонними лавинами, що виникають в іскрових каналах, де тиски збільшуються до сотень атмосфер, а температура підвищується до 10000°С. Яскравий приклад - блискавка; 4) коронний – тип газового розряду, що виникає в сильних неоднорідних електричних полях навколо електродів із великою кривизною в газах із доволі високою густиною. Утворюється у тих випадках коли напруга є недостатньою, щоб пробити розрядний проміжок. Тому біля вістрів виникає частковий пробій, який називається коронний. Самостійно почитати Савельєва про розряди. Явище самоіндукції Суть явища полягає у виникненні електрорушійної сили індукції при зміні власного магнітного поля контуру. Якщо, по контуру протікає електричний струм І, то при цьому контурну площадку пронизує певний магнітний потік. Величина магнітного поля тим більша, чим більший електричний стум(
Fig 70 Ми отримали, що L=Ф, якщо І=1, тобто L- індуктивність контура чисельно рівна магнітному потокові, який пронизує контур при протіканні по контуру струму величиною в 1А. Якщо вважати В сталим, то зміна Ф може проходити лише за рахунок струму І, а тому Звідси L чисельно рівний Індуктивність соленоїда:
Fig.71
Ф1(один виток пронизує потік)=BS, де S- площа, яку обмежує один виток.
Енергія магнітного поля Спадання струму в колі з індуктивністю:
Fig 72 Якщо включити ключ в положення 1,то в колі протікатиме струм І0: Якщо ключ перевести в положення 2 (розірвати коло), записавши 2-ге правило Кірхгофа отримаємо: Використавши початкові умови, одержимо t=0, I=I0 (в момент вимкнення); t=0,
Fig 73 Наростання струму в колі з індуктивнівстю: Вмикаємо коло, і при t=0, I=0. Використовуючи друге правило Кірхгофа запишемо наступне рівняння:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.144.139 (0.011 с.) |



 .
.
 -А2,1
-А2,1
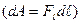
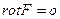
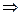

 - оператор Набла
- оператор Набла  - оператор Лапласа.
- оператор Лапласа. В них робота залежить від шляху, тобто
В них робота залежить від шляху, тобто  .
.
 - сила притягання двох мас по 1 кг на відстані 1м.
- сила притягання двох мас по 1 кг на відстані 1м. - закон Кулона.
- закон Кулона. ;
;
 , де
, де  - електрична стала (
- електрична стала ( ).
). )
)

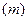 з точки 1 в точку 2. (Припустимо, що заряди відштовхуються)
з точки 1 в точку 2. (Припустимо, що заряди відштовхуються) ;
; ;
; (наскільки заряд
(наскільки заряд  за час траєкторії
за час траєкторії  ).
).

 ;
;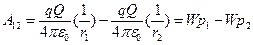 - робота по переміщенню заряда з точки 1 в точку 2.
- робота по переміщенню заряда з точки 1 в точку 2. дорівнює векторній сумі напруженостей полів, створених в даній точці кожним джерелом:
дорівнює векторній сумі напруженостей полів, створених в даній точці кожним джерелом:  .
.
 , яка є скалярною.
, яка є скалярною.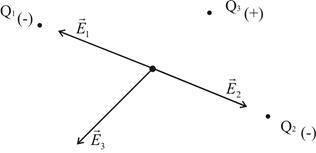
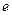 , а носієм позитивного заряду протони
, а носієм позитивного заряду протони 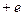 .
.  Кл – елементарний заряд.
Кл – елементарний заряд. - зв’язок напруженості та потенціалу з зарядом
- зв’язок напруженості та потенціалу з зарядом
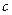 , і фактично є коефіцієнтом пропорційності між зарядом і потенціалом:
, і фактично є коефіцієнтом пропорційності між зарядом і потенціалом:  .
.  , якщо
, якщо  ,
,  (чисельно ємність рівна заряду, який потрібно надати тілу, щоб змінити потенціал на 1).
(чисельно ємність рівна заряду, який потрібно надати тілу, щоб змінити потенціал на 1). Ф
Ф 

 – ємність сфери.
– ємність сфери.


 -ємність сферичного конденсатора
-ємність сферичного конденсатора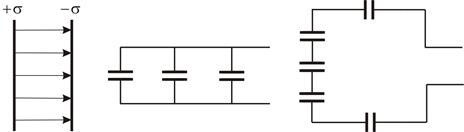


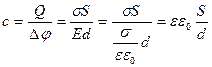 - ємність плоского конденсаора.
- ємність плоского конденсаора. - сумарна ємність при паралельному з’єднанні конденсаторів
- сумарна ємність при паралельному з’єднанні конденсаторів - сумарна ємність при послідовному з’єднанні конденсаторів
- сумарна ємність при послідовному з’єднанні конденсаторів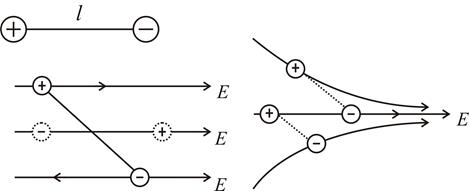
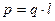 – дипольний момент.
– дипольний момент.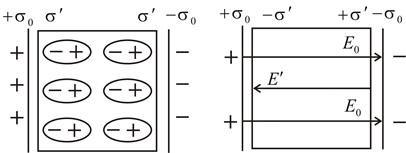
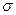 . Таким чином, якщо поле створюється вільними зарядами
. Таким чином, якщо поле створюється вільними зарядами 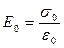 , то зв’язані заряди створюють зворотні поля
, то зв’язані заряди створюють зворотні поля 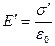 ,тобто в діелектрику виникає поле
,тобто в діелектрику виникає поле
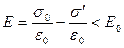
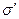 можна використати наступні думки:
можна використати наступні думки: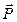 , який називається вектором поляризації і
, який називається вектором поляризації і 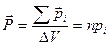 , де n-концентрація елементарних диполів,
, де n-концентрація елементарних диполів, 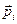 -елементарні дипольні моменти,
-елементарні дипольні моменти, 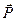 -дипольний момент одиниці об’єму. Можна показати, що
-дипольний момент одиниці об’єму. Можна показати, що 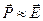 і
і  æ
æ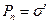 (нормальна складова вектора поляризації рівна поверхневій густині зв’язаного заряду).
(нормальна складова вектора поляризації рівна поверхневій густині зв’язаного заряду).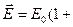 æ)-1
æ)-1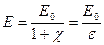 .
.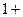 æ
æ  - відносна діелектрична проникність діелектрика, і вона показує в скільки разів електричне поле діелектрика має напруженість меншу, ніж напруженість поля у вакуумі.
- відносна діелектрична проникність діелектрика, і вона показує в скільки разів електричне поле діелектрика має напруженість меншу, ніж напруженість поля у вакуумі. (закон Кюрі) для речовин, молекули яких полярні.
(закон Кюрі) для речовин, молекули яких полярні.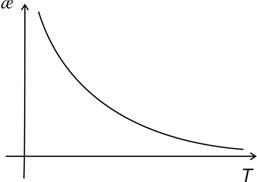
 (порядку 103). Завдяки цьому у них спостерігається дуже цікава картина поляризації (в них наявний гістерезис поляризації).
(порядку 103). Завдяки цьому у них спостерігається дуже цікава картина поляризації (в них наявний гістерезис поляризації).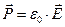 æ. В сегнетоелектрика æ= æf(E).
æ. В сегнетоелектрика æ= æf(E).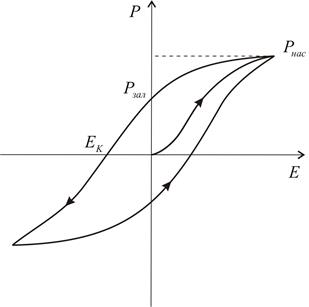
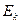 - коерцитивна сила.
- коерцитивна сила. → Мæ
→ Мæ 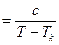 – закон Кюрі-Вейса
– закон Кюрі-Вейса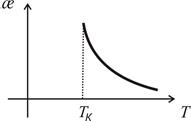

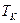 ) пояснюють так: при
) пояснюють так: при  домени руйнуються і сегнетоелектрик стає звичайним діелектриком.
домени руйнуються і сегнетоелектрик стає звичайним діелектриком.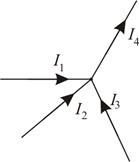

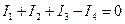

 .
.




 – питомий опір металів лінійно залежить від
– питомий опір металів лінійно залежить від  , таким чином:
, таким чином:  , де
, де  – питомий опір при
– питомий опір при 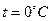 ,
,  .
.
 – температурний коефіцієнт опору. Показує відносну зміну опору при зміні температури на
– температурний коефіцієнт опору. Показує відносну зміну опору при зміні температури на  . В більш широкому діапазоні температур
. В більш широкому діапазоні температур  не можна вважати сталим, бо температурна залежність опору металів не завжди лінійна:
не можна вважати сталим, бо температурна залежність опору металів не завжди лінійна:  .
.  – абсолютна температура в шкалі Кельвіна.
– абсолютна температура в шкалі Кельвіна.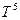 , а при температурах вищих за температуру Дебая (
, а при температурах вищих за температуру Дебая ( ) – еквівалентний
) – еквівалентний  .
.

 ,
,  (опір прямує до залишкового по закону
(опір прямує до залишкового по закону  Кл Виявилось, що не було ніякого проникнення металу в метал. Так прийшли до висновку, що носіями струму в металі не можуть бути іони металу. З’явилась думка, що носіями струму можуть бути вільні електрони.
Кл Виявилось, що не було ніякого проникнення металу в метал. Так прийшли до висновку, що носіями струму в металі не можуть бути іони металу. З’явилась думка, що носіями струму можуть бути вільні електрони.

 . Зразок металу рухаємо з великою швидкістю
. Зразок металу рухаємо з великою швидкістю  , а потім швидко (різко) гальмуємо. Внаслідок цього носії струму всередині зразка рухаються по інерції, тобто по зразку протікає струм (котушка і токарний верстат, крутильні коливання
, а потім швидко (різко) гальмуємо. Внаслідок цього носії струму всередині зразка рухаються по інерції, тобто по зразку протікає струм (котушка і токарний верстат, крутильні коливання  , то на електрони діє сила
, то на електрони діє сила  і під дією цієї сили вони рухаються з прискоренням
і під дією цієї сили вони рухаються з прискоренням  . Вважається, що кожен електрон пролітає в середньому відстань
. Вважається, що кожен електрон пролітає в середньому відстань  до наступного зіткнення з кристалічною граткою.
до наступного зіткнення з кристалічною граткою. 
 – час між двома послідовними зіткненнями.
– час між двома послідовними зіткненнями. – середня швидкість напрямленого руху носіїв.
– середня швидкість напрямленого руху носіїв.



 – стала Больцмана,
– стала Больцмана,  Тому
Тому 

 за 1 с електрон зазнає
за 1 с електрон зазнає  зіткнень. Таким чином,
зіткнень. Таким чином,  електронів виділяють в одиниці об’єму енергію:
електронів виділяють в одиниці об’єму енергію:

 Ǻ де 1 Ǻ =10-10 м. В той час, як відстань між сусідніми атомами рівна
Ǻ де 1 Ǻ =10-10 м. В той час, як відстань між сусідніми атомами рівна  Ǻ.
Ǻ. Ǻ електрон повинен пролітати біля декількох сотень атомних відстаней без зіткнень, що малоймовірно.
Ǻ електрон повинен пролітати біля декількох сотень атомних відстаней без зіткнень, що малоймовірно.
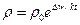

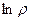 як функції
як функції 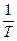 і
і  , як
, як  , то отримаємо наступні залежності:
, то отримаємо наступні залежності:


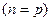 називають власною провідністю напівпровідника.
називають власною провідністю напівпровідника. ). Якщо домішка має меншу валентність (наприклад 3), то в атомі домішки не вистачає електрона для створення хімічного зв’язку. В результаті може виникнути додаткова дірка. Така домішка є акцепторна(
). Якщо домішка має меншу валентність (наприклад 3), то в атомі домішки не вистачає електрона для створення хімічного зв’язку. В результаті може виникнути додаткова дірка. Така домішка є акцепторна( ), а провідність дірковою.
), а провідність дірковою. називається енергією активації провідності.
називається енергією активації провідності. 
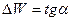 – енергія активації. Дані висновки є справедливі і для провідності діелектриків, однак якщо в напівпровіднику енергія активації не більше 2 еВ то для діелектрика вона може бути і 4-6 еВ. Провідність діелектрика можна підвищити, ввівши домішки. Введення домішок називається легуванням.
– енергія активації. Дані висновки є справедливі і для провідності діелектриків, однак якщо в напівпровіднику енергія активації не більше 2 еВ то для діелектрика вона може бути і 4-6 еВ. Провідність діелектрика можна підвищити, ввівши домішки. Введення домішок називається легуванням.


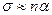 , тут
, тут  росте з ростом температури і є в межах
росте з ростом температури і є в межах  .
.

 , де k – стала Больцмана).
, де k – стала Больцмана).
 )
)
 ,
,  , де L - певний коефіцієнт пропорційності, який залежить від геометрії контура і від магнітних властивостей середовища.
, де L - певний коефіцієнт пропорційності, який залежить від геометрії контура і від магнітних властивостей середовища. ; то
; то  .
. , якщо
, якщо 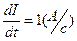 (швидкість зміни струму)
(швидкість зміни струму)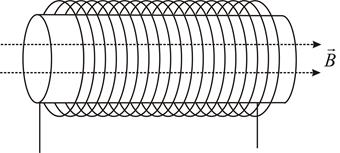
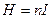 ;
; 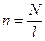
 - довжина котушки;
- довжина котушки; 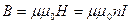
 ;
; 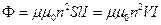 ;
;  , тут
, тут 
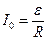 .
. .
. . Або
. Або  ; де
; де  - постійна часу; і якщо
- постійна часу; і якщо  ,то ми отримаємо в
,то ми отримаємо в 

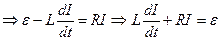 . Тоді
. Тоді  , де
, де  -
- 


