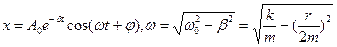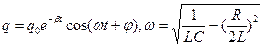Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики гармонічних коливаньСодержание книги
Поиск на нашем сайте
1)Амплітуда коливань – найбільше відхилення від положення рівноваги; 2) В момент часу t=0, 3)Величина Т називається періодом коливань – час протягом якого здійснюється одне повне коливання; 4) 5)
Вільні гармонічні коливання Розглянемо коливання які відбуваються під дією пружної та квазіпружної сили. Задача 1:
Fig 87
Задача 2: (математичний маятник) рух типу обертового
Fig 88
Якщо кут
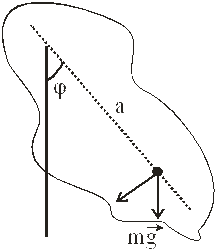
Задача 3: (фізичний маятник) – довільне тверде тіло, яке може коливатись відносно осі, що не проходить через центр мас цього тіла.
Fig 89
L- зведена довжина фізично маятника – довжина такого математичного маятника який коливається з цієюж частотою, що і даний фізичний маятник.
Задача 4: (коливання в коливальному контурі)
Fig 90 R=0 – коливальний контур без втрат
Fig 91
При t=0,
Fig 92
Енергія коливань Покажемо, що в коливальних системах без втрат виконується закон перетворення механічної енергії, причому в механічних коливаннях максимальна кінетична енергія прейде в потенціальну, і навпаки. В коливальному контурі енергія електричного поля С перетворюється в енергію магнітного поля котушки L, і навпаки.
Сумарна енергія:
Для коливального контуру:
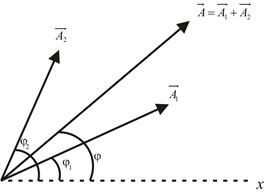
Cкладання коливань 1)Складання коливань одного напрямку; а) складання коливань однакової частоти.
................................
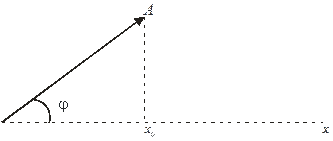
Для складання коливань одного напрямку і одної частоти використовують метод вектора амплітуди: будують вектор по величині рівний амплітуді з кутом рівним початковій фазі. При t=0,
Fig 93 Якщо розпочати обертати вектор А з кутовою швидкістю проти годинникової стрілки, то в певний момент часу проекція А на вісь х дає миттєве значення х. Період коливань рівний часу одного обертання. За даним методом складання коливань зводиться до складання відповідних векторів амплітуди.
Fig 94
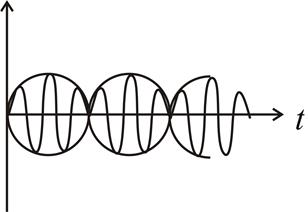
Кінцеве б)складання коливань з близькими частотами
сумарне коливання називається биттям і виглядає так:
Fig 95 2) Складання взаємноперпендикулярних коливань. Фігури Лісажу Треба знайти суму коливань однієї частоти, взаємноперпендикулярних напрямів
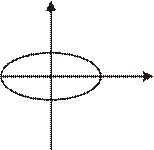
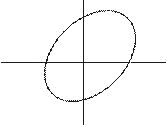
α = 0 α = π α = Отже, в загальному випадку в нас є еліпс: При a = b рух по еліпсу вироджується в рух по колу. Якщо частоти неоднакові, то рух дуже складний, якщо частоти кратні, то вийдуть фігури, які можна наперед вгадати, вони називаються фігурами Ліссажу.
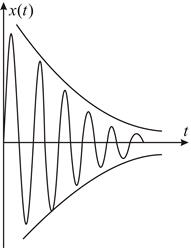
Fig 96 Згасаючі коливання (коливання при наявності втрат)
Тоді рівняння руху запишеться як:
Fig 97 виходимо з другого правила Кірхгофа:
Підставляємо дані рівності і отримаємо:
Fig 98 Як бачимо з графіку, огинаюча є експонентою.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.249.119 (0.009 с.) |

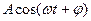
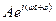
 - фаза коливання;
- фаза коливання;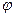 - початкова фаза.
- початкова фаза.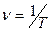 - частота коливань, кількість коливань за одиницю часу;
- частота коливань, кількість коливань за одиницю часу;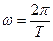 - кругова (циклічна) частота
- кругова (циклічна) частота 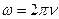 .
.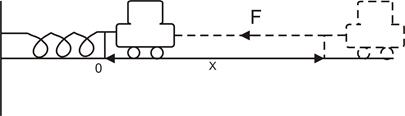
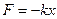 (закон Гука)
(закон Гука)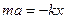 (задача одномірна)
(задача одномірна)
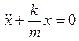
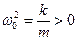
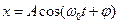 - рівняння коливань, тут
- рівняння коливань, тут 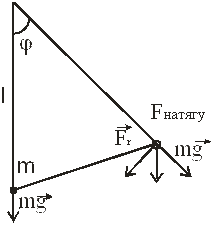
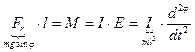

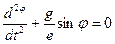


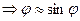
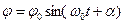
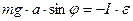
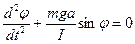
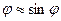


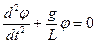
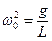
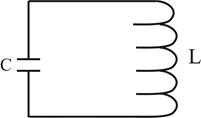
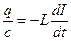
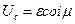 ?
?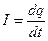
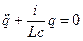
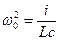



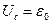 . Вмомент часу t=0 переводимо ключ з положення 1 в положення 2. З цього моменту починається розрядка конденсатора через котушку. Індуктивність стримує розрядний струм, тому він наростає поступово. Коли конденсатор розрядиться, струм має найбільше значення; якщо б не було індуктивності струм би зник, однак
. Вмомент часу t=0 переводимо ключ з положення 1 в положення 2. З цього моменту починається розрядка конденсатора через котушку. Індуктивність стримує розрядний струм, тому він наростає поступово. Коли конденсатор розрядиться, струм має найбільше значення; якщо б не було індуктивності струм би зник, однак 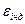 самоідукції підтримує його протікання в колі, струм повільно спадає до нуля. В результаті цього, проходить перезарядка конденсатора в зворотньому напрямі. На той момент, коли струм зникає, конденсатор набуває того ж заряду тільки протилежної полярності. Після цього починається зворотній цикл.
самоідукції підтримує його протікання в колі, струм повільно спадає до нуля. В результаті цього, проходить перезарядка конденсатора в зворотньому напрямі. На той момент, коли струм зникає, конденсатор набуває того ж заряду тільки протилежної полярності. Після цього починається зворотній цикл.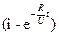 - гармонічний закон в колі. Роль пружної сили відіграє напруга на конденсаторі.
- гармонічний закон в колі. Роль пружної сили відіграє напруга на конденсаторі.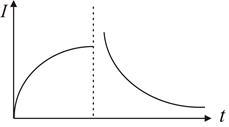
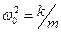
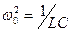
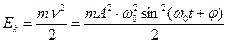 - кінетична енергія коливань;
- кінетична енергія коливань; - потенціальна енергія коливань.
- потенціальна енергія коливань.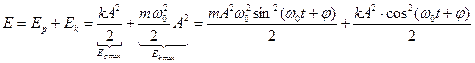

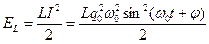
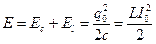
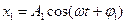

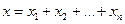
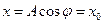


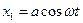



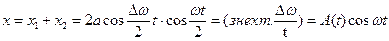
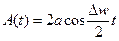
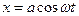
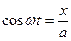
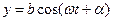
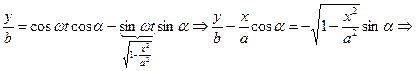
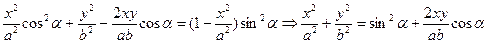
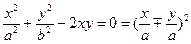
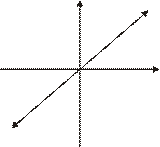

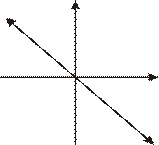
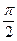
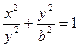
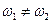 :
: 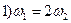
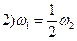



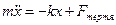 - рівняння згасаючих коливань.
- рівняння згасаючих коливань.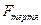 протилежна до швидкості: вважатимемо, що
протилежна до швидкості: вважатимемо, що 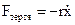
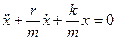 . Позначимо
. Позначимо 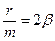 і
і  . Тоді перепишемо рівняння руху
. Тоді перепишемо рівняння руху 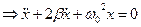 . Для коливного контура
. Для коливного контура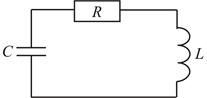
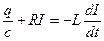
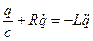
 . Позначимо
. Позначимо  . Розв’язок цього рівняння шукаємо в такому вигляді:
. Розв’язок цього рівняння шукаємо в такому вигляді: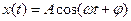

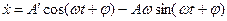
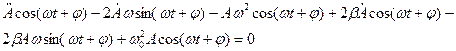
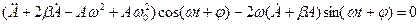
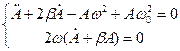
 , при t = 0
, при t = 0 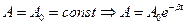 ,
, 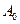 - початкова амплітуда. Підставимо в перше рівняння:
- початкова амплітуда. Підставимо в перше рівняння: 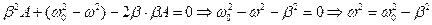 . При наявності опору частота коливань зменшується. Зокрема, якщо опір дуже великий коливання взагалі зникають, і є аперіодичне (неперервне) наближення системи до положення рівноваги.
. При наявності опору частота коливань зменшується. Зокрема, якщо опір дуже великий коливання взагалі зникають, і є аперіодичне (неперервне) наближення системи до положення рівноваги.