
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Змінний електричний струм як вимушені електричні коливанняСодержание книги
Поиск на нашем сайте
Струми, які ми будемо розглядати можна вважати як квазістаціонарні явища, тобто не треба враховувати ефектів, пов’язаних із зміною фази коливань протягом часу поширення коливань.
Тоді 1) Протікання змінного струму через опір R
Fig 101
Fig 102
Тобто, можна ствердити, що коливання струму і напруги проходить в однаковій фазі. 2) Конденсатор в колі змінного струму
Fig 103
То
Струми на ємності випереджають напругу на
Fig 104 3) Індуктивність в колі змінного струму Вважатимемо, що R = 0
Fig 105
Отже струм в котушці відстає від напруги на
Fig 106
4) Закон Ома для послідовного з’єднання в колі змінного струму
Fig 107 Векторна діаграма:
Fig 108
Спільним для даного кола є струм. Напруга на опорі в тій же фазі що і струм
Між сумарною напругою і струмом існує зсув фаз на кут φ, який визначатиметься так: Ми можемо записати закон Ома для змінного струму:
Fig 109 5) Закон Ома для паралельного з’єднання в колі змінного струму (буде все подібно до попереднього випадку, з тою різницею, що спільною буде напруга).
Fig 110 Векторна діаграма:
Fig 111
6) Резонанс струмів та напруг
Fig 112 Беремо послідовне з’єднання
Fig 113 В паралельному колі виникає явище резонансу струмів. Воно проявляється в тому, що при даній фіксованій напрузі сумарний струм в колі досягає найменших значень:
Fig 114 Котушка сама по собі має опір і на ній існує зсув фаз, тому навіть при резонансі сумарний струм не дорівнює нулю.
Fig 115 Резонанс струмів проявляється найменшим значенням сумарного струму.
Потужність в колі змінного струму Для постійного струму Для змінного струму можна записати вираз для миттєвої потужності
Одержали, що потужність в колі змінного струму буде найбільшою тоді, коли зсув фаз між струмом і напругою є відсутній. сosφ – коефіцієнт потужності.
Fig 116 Ефективне значення струму чи напруги - значення такого постійого струму чи напруги, що дають ту саму теплову дію, що і даний змінний струм.
Хвилі Хвиля – процес поширення коливань у просторі. Ми будемо розглядати поширення гармонічних коливань у просторі, пам’ятаючи, що коливання іншої форми можна представити як суперпозицію гармонічних коливань різних частот. 1) Хвилі подібно як і коливання залежать від природи. 2) Можуть бути поперечні чи поздовжні. Поперечна хвиля - така хвиля в якій напрямок коливань фізичної величини перпендикулярний до напрямку поширення хвилі. Повздовжня хвиля – така хвиля, коли коливання фізичної величини співпадають за своїм напрямком з напрямком поширення хвилі. Звукові хвилі є поздовжні: Електромагнітна хвиля – лише поперечна. 3) Основні характеристики хвиль: Властивості хвиль даної природи залежать від їх частоти і періоду.
Хвильова поверхня – це є геометричне місце точок, в яких коливання проходить в однаковій фазі. Фронт хвилі – геометричне місце точок до яких коливання дійшли до даного моменту часу. Фронт хвилі є також хвильовою поверхнею. λ – довжина хвилі v – фазова швидкість – швидкість поширення даної фази. v є фактично швидкістю руху фронту хвилі в напрямку поширення хвилі. Найпростішими прикладами хвильових поверхонь є плоска хвиля (хвильова поверхня – площина) і сферична хвиля (хвильова поверхня – сфера).
Fig 117 Обов’язковою умовою для плоскої хвилі є те, що швидкість перпендикулярна до фронту хвилі. Відстань, яку проходить хвиля за один період називають довжиною хвилі і позначають Рівняння хвиль
Треба вивести функцію · якщо · якщо З цього аналізу випливає, що рівнянням хвилі має бути період, фактично як по часу так і по координаті. Виведемо рівняння плоскої хвилі а) хвиля поширюється вздовж осі х
Fig 118 Коливання здійснюються за законом б) хвиля поширюється в довільному напрямі:
Fig 119 Описати коливний процес в межах коливної поверхні:
Рівняння сферичної хвилі:
Хвильове рівняння Хвильове рівняння - це таке диференціальне рівняння, розв'язком якого є рівняння хвилі.
Візьмемо другі похідні по всіх напрямках:
Одержали наступне рівняння:
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |


 ~
~  (досить малий час, тому можемо вважати, що в межах електричного кола всі процеси проходять таким чином, що сигнал доходить в усі точки кола майже моментально).
(досить малий час, тому можемо вважати, що в межах електричного кола всі процеси проходять таким чином, що сигнал доходить в усі точки кола майже моментально).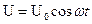 , де
, де  - циклічна частота коливань.
- циклічна частота коливань.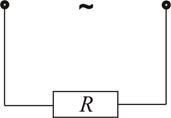
 , де
, де  . Векторна діаграма процесу:
. Векторна діаграма процесу:

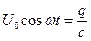 (друге правило Кірхгофа);
(друге правило Кірхгофа); ;
; - ємнісний опір кола;
- ємнісний опір кола; ,
, 
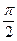 . Векторна діаграма:
. Векторна діаграма:

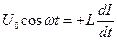





 .
.
 .
. - цей вираз називається законом Ома для послідовного з’єднання в колі змінного струму.
- цей вираз називається законом Ома для послідовного з’єднання в колі змінного струму.  ,
,  ,
,  - сумарний опір кола. Якщо немає ємності, то
- сумарний опір кола. Якщо немає ємності, то 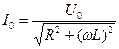 , а
, а  . Векторна діаграма:
. Векторна діаграма: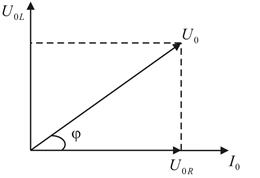


 , Далі всі розрахунки проводимо по аналогії до пункту 4.
, Далі всі розрахунки проводимо по аналогії до пункту 4.
 ; зсув фаз рівний нулеві (
; зсув фаз рівний нулеві ( ).При резонансі струм найбільший. Дане явище дістало назву резонанс напруг тому, що
).При резонансі струм найбільший. Дане явище дістало назву резонанс напруг тому, що  , але перебувають в протифазі і взаємно компенсуються. Подібні резонансні криві можна одержати змінюючи с та L.
, але перебувають в протифазі і взаємно компенсуються. Подібні резонансні криві можна одержати змінюючи с та L.
 , (
, ( ). Струми
). Струми  і
і  рівні за величиною і тому взаємокомпенсуються. Якби не було R, то струм в колі був би 0. (при великих струмах через с і L). Реальне коло обов’язково має електричний еквівалент.
рівні за величиною і тому взаємокомпенсуються. Якби не було R, то струм в колі був би 0. (при великих струмах через с і L). Реальне коло обов’язково має електричний еквівалент.


 ,
,  .
. . Шукаємо середнє значення потужності за період:
. Шукаємо середнє значення потужності за період: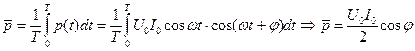
 - амплітудні значення напруги та струму.
- амплітудні значення напруги та струму.  ,
, 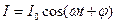 , вводять
, вводять 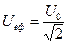 ,
,  , тоді
, тоді  .
.
 ,
, 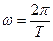



 ,
,  . Довжина хвилі – найменша відстань між двома хвильовими поверхнями в яких коливання проходять в однаковій фазі.
. Довжина хвилі – найменша відстань між двома хвильовими поверхнями в яких коливання проходять в однаковій фазі. , яка б повністю описувала коливний процес хвилі,і яка має мати наступні властивості:
, яка б повністю описувала коливний процес хвилі,і яка має мати наступні властивості: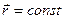 , то функція має перейти в рівняння коливань в даній точці тобто функцію типу
, то функція має перейти в рівняння коливань в даній точці тобто функцію типу  А cos (ωt+φ), φ(r).
А cos (ωt+φ), φ(r).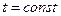 , то рівняння хвилі має дати миттєву картину коливного процесу у всьому просторі.
, то рівняння хвилі має дати миттєву картину коливного процесу у всьому просторі.
 . Ми хочемо описати коливання в точці х. Коливання в точці х буде відставати:
. Ми хочемо описати коливання в точці х. Коливання в точці х буде відставати: 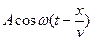 . Стверджуємо, що f(x,t) визначатиметься наступним чином:
. Стверджуємо, що f(x,t) визначатиметься наступним чином: 
 ,
,  - хвильове число. Якщо хвиля зворотня, то буде
- хвильове число. Якщо хвиля зворотня, то буде  .
.
 - співпадають,
- співпадають, 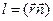 . Проектуємо
. Проектуємо  на напрямок нормалі і одержимо:
на напрямок нормалі і одержимо: - рівняння плоскої хвилі, яка поширюється в будь – якому напрямку;
- рівняння плоскої хвилі, яка поширюється в будь – якому напрямку;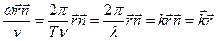 ,
,  - хвильовий вектор.
- хвильовий вектор. .
. - рівняння плоскої хвилі;
- рівняння плоскої хвилі; - рівняння сферичної хвилі.
- рівняння сферичної хвилі.

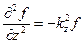




 - хвильове рівняння.
- хвильове рівняння.


