
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знаходження змінного струму. Миттєве і максимальне значення е. р. с.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В провіднику при перетині ним магнітних силових ліній виникає е. р. с. індукції, величина якої дорівнює добутку індукції поля на довжину провідника, на швидкість руху провідника і на синус кута між напрямами вектора магнітної індукції і вектора швидкості:
ω— циклічна частота змінного струму. Величину ε0 називають максимальним, або амплітудним, значенням е. р. с. Якщо рамка складається з N витків, то е. р. с, яка виникає в ній при рівномірному обертанні, буде в N раз більша
Якщо рамку замкнути на зовнішнє коло з опором R, в зовнішньому колі проходитиме змінний струм
який буде зареєстрований гальванометром. Величина I називається миттєвим значенням струму, а I0 — максимальним, або амплітудним. Змінним струмом називають струм, який змінюється за величиною і напрямом за синусоїдним законом. Амплітуда, період, частота і фаза змінного струму. Ефективне (діюче) значення струму і напруги Найбільші значення струму I0 і ε0 називаються амплітудними. Час повної зміни е. р. с. (циклу), після якого весь процес її зміни повторюється в тому самому порядку, називається періодом змінного струму (Т). Число періодів змінного струму за одиницю часу називають частотою змінного струму ν:
Стандартна частота змінного струму 50 Гц. Величину Ефективне (діючє) значення струму:
Ефективним, або діючим, значенням сили змінного струму називається сила такого постійного струму, який виділяє в певному провіднику стільки ж теплоти за час одного періоду змінного струму, скільки останній за той самий час. Ефективні значення напруги Uеф і εеф менші від максимальних (амплітудних) в
Потужність змінного струму визначається добутком
де φ — різниця фаз між струмом і е. р. с. Визначену таким способом потужність називають ефективною. Величина cosφ називається коефіцієнтом потужності. Опори в колі змінного струму Якщо в колі змінного струму є лише активний опір R, то вся електрична енергія витрачається на теплову дію. У цьому колі струм і напруга завжди мають однакові фази. Закон Ома в цьому разі справедливий як для максимальних, так і для діючих значень напруги і сили струму:
Індуктивний опір прямо пропорційний індуктивності кола L і циклічній частоті змінного струму ω:
Ємнісний опір Хс обернено пропорційний ємності С і циклічній частоті змінного струмуω:
Індуктивний і ємнісний опори називають реактивними. Якщо коло складається з послідовно сполучених активного, індуктивного і ємнісного опорів, то повний опір кола Z можна визначити за формулою: Зсув фаз між струмом і напругою в колі змінного струму визначають з рівності
Закон Ома для кола з трьох послідовно сполучених опорів R, Хl і Хс визначається співвідношенням
Трансформатори
Для змінного струму е. р. с. (напругу) підвищують за допомогою підвищувальних трансформаторів. У найпростішому вигляді трансформатор складається з двох обмоток на спільному замкнутому залізному осерді. Первинна обмотка N1 складається з невеликого числа витків товстого проводу, вторинна обмотка N2 — з великого числа витків тонкого проводу. Струм, що проходить через обмотку N1, створює змінний потік магнітної індукції Ф, який майже цілком зосереджений всередині осердя і пронизує витки вторинної обмотки. Обидві обмотки пронизуються тим самим потоком. При зміні цього потоку в кожній обмотці індукується е. р. с. Якщо N1 — число витків первинної обмотки, то е. р. с, яка виникає, дорівнює
У вторинній обмотці, що має N 2 витків, виникає е. р. с, яка дорів- нює
Порівнявши вирази для ε1 і ε2, дістанемо зв'язок
Відношення (N1> N2), то трансформатор називається знижувальним. Якщо до кінців вторинної обмотки трансформатора не під'єднане яке-небудь навантаження, тобто вторинна обмотка розімкнута (холостий хід трансформатора), то напруга на кінцях цієї обмотки і U2 дорівнює е. р. с. ε2, що індукується в ній:
Е. р.с. ε1,яка індукується в первинній обмотці, напрямлена, за правилом Ленца, протилежно до прикладеної до неї зовнішньої напруги U2 і майже дорівнює їй:
Отже, відношення індукованих е. р. с. в обмотках при холостому ході наближено дорівнює відношенню напруг на затискачах обмоток трансформатора:
Якщо вторинну обмотку тепер замкнути на яке-небудь зовнішнє навантаження, то напруга на затискачах цієї обмотки вже дорівнюватиме
де Осердя трансформатора виготовляють не з цільного куска заліза, а набирають з тонких пластин, ізольованих одна від одної шаром лаку або тонкого паперу. Це спричинено тим, що змінний магнітний потік, який існує в трансформаторі, створює е. р. с. індукції не лише у витках котушок, а й в осерді, яке також є провідником. Тому в осерді виникають вихрові струми, які називають струмами Фуко. Ці струми нагрівають осердя, що призводить до непродуктивних втрат енергії. Щоб зменшити ці втрати, осердя трансформатора набирають з окремих, ізольованих одна від одної, пластин. Нехтуючи втратами в трансформаторі, можна вважати, що потужності, які розвиваються в первинному і вторинному колах, практично однакові:
Використавши попередню рівність (1), дістанемо
Сили струмів у первинному і вторинному колах обернено пропорційні числу витків у первинній і вторинній обмотках.
Приклади рішення задач Приклад 1. По відрізку прямого дроту довжиною l =80см тече струм І =50А. Визначити магнітну індукцію В поля, створеного цим струмом, у точці А, рівновіддаленої від кінців відрізка дроту і знаходиться на відстані r 0=30см від його середини.(рис.2)
де символ l означає, що інтегрування поширюється на всю довжину дроту. Запишемо закон Біо-Савара-Лапласа у векторній формі:
де dВ — магнітна індукція,створена елементом дроту довжиною dl зі струмом І у точці, обумовленій радіусом-вектором r; m0 - магнітна постійна; m, — магнітна проникність середовища, у якій знаходиться дріт (у нашому випадку m=1). Помітимо, що вектори dВ від різних елементів струму співпадають за напрямком, тому вираз (1) можна переписати в скалярній формі:
де В скалярному вираженні закону Біо-Савара-Лапласа кут a є кут між елементом струму Іdl і радіус-вектором r. Таким чином,
Перетворимо підінтегральний вираз так, щоб була одна перемінна — кут a. Для цього виразимо довжину елемента дроту dl через кут da: у вигляді
Таким чином, вираз (2) можна переписати у вигляді
де a1 і a2 – межі інтегрування. Виконаємо інтегрування
Помітимо, що при симетричному розташуванні точки А щодо відрізка дроту cosa2 = -cosa1. З урахуванням цього формула (3) прийме вигляд
З рис. 2 випливає що;
Підставивши вираз cosa1 у формулу (4), одержимо
Зробивши обчислення по формулі (5), знайдемо В=26,7мкТл. Напрямок вектора магнітної індукції В поля, створеного прямим струмом, можна визначити за правилом буравчика (правила правого гвинта). Для цього проводимо магнітну силову лінію (штрихова лінія на рис. 3) і по дотичній до неї в цікавлячій нас точці проводимо вектор В. Вектор магнітної індукції В в точці А (рис. 4) спрямований і перпендикулярно площині креслення від нас.
Приклад 2. Два паралельних нескінченно довгих проводи D і С, по яких тече в одному напрямку електричний струм силою І =60А, розташовані на відстані d =10cм один від одного. Визначити магнітну індукцію В поля, створеного провідниками зі струмом у точці А (рис. 4), що відстоїть від вісі одного провідника на відстані r 1=5см, від іншого — r 1=12см. Рішення. Для визначення магнітної індукції В в точці А скористаємося принципом суперпозиції магнітних полів. Для цього визначимо напрямки магнітних індукцій В 1, і В 2 полів, створених кожним провідником зі струмом окремо, і складемо їх геометрично: В=В1+В2. Модуль вектора В може бути знайдений по теоремі косинусів:
де a— кут між векторами B1 і В2. Магнітні індукції B1 і В2 виражаються відповідно через силу струму І і відстані r 1 і r 2 від проводів до точки А:
Підставляючи вираз B 1 і В 2 у формулу (1) і виносячи
Обчислимо cos a. Помітивши, що a=ÐDAC (так як кути з відповідно перпендикулярними сторонами), за теоремою косинусів запишемо
де d — відстань між проводами. Звідси
Підставимо у формулу (2) числові значення фізичних величин і зробимо обчислення:
Приклад 3. По тонкому провідному кільцю радіусом R =10см тече струм І = 80А. Знайти магнітну індукцію В в точці А, рівновіддаленій від усіх точок кільця на відстань r =20см. Рішення. Для рішення задачі скористаємося законом Біо — Савара — Лапласа:
де dВ — магнітна індукція поля, створеного елементом струму Іdl точці, обумовленої радіусом вектором r. Виділимо на кільці елемент dl і від нього в точку А проведемо радіус-вектор r (рис. 5). Вектор dВ направимо відповідно до правила буравчика. Відповідно до принципу суперпозиції магнітних полів, магнітна індукція В в точці А визначається інтегруванням:
де інтегрування ведеться по всіх елементах dl. Розкладемо вектор dВ на дві складові: dB ^, перпендикулярну площині кільця, і dB ||, паралельно площині кільця, тобто
Тоді
Помітивши, що
Після скорочення на 2π і заміни cosb на R / r (рис.5) одержимо
Перевіримо, чи дає права частина рівності одиницю магнітної індукції (Тл):
Тут ми скористалися визначальною формулою для магнітної індукції:
Тоді . Виразимо усі величини в одиницях СІ і зробимо обчисленння
чи В=62,8мкТл. Вектор В спрямований по вісі кільця (пунктирна стрілка на рис. 5) відповідно до правила свердлика.
Приклад 4. Довгий провід зі струмом І= 50А згинають під кутом a=2p/3. Визначити магнітну індукцію В в точці А (рис. 6). Відстань d =5 см. Рішення. Вигнутий провід можна розглядати як два довгих проводи, кінці яких з'єднані в точці О (рис.6). Відповідно до принципу суперпозиції магнітних полів магнітна індукція В в точці А буде дорівнювати геометричній сумі магнітних індукцій B1 і В2 полів, створених відрізками довгих проводів 1 до 2, тобто B=B1 + B2. Магнітна індукція В 2 дорівнює нулю. Це випливає з закону Біо—Савара—Лапласа, відповідно до якого в точках, що лежать на вісі приводу, dВ=0 ([dlr]=0). Магнітну індукцію В 1 знайдемо, скориставшись співвідношенням (3), знайденим у прикладі 1:
де r 0 — найкоротша відстань від дроту 1 до точки А (рис. 7).
У нашому випадку Тоді магнітна індукція
Так як В=В1 (В2 =0), то
Вектор В співпадає по напрямку з вектором B 1 і визначається правилом правого гвинта. На (рис. 7) цей напрямок відзначений хрестиком у кружечку (перпендикулярно площини креслення, від нас). Перевірка одиниць аналогічна виконаної в прикладі 3. Зробимо обчислення:
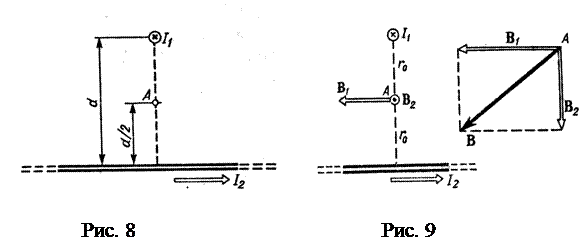
Приклад 5. Два нескінченно довгих проводи схрещені під прямим кутом (рис. 8). По проводах течуть струми І1 =80 А та І2 =60 А. Відстань d між проводами дорівнює 10 см. Визначити магнітну індукцію В в точці А, однаково віддаленої від обох проводів.
В 2 — магнітна індукція поля, створеного в точці А струмом І 2. Помітимо, що вектори B 1 і В 2 взаємно перпендикулярні (їхні напрямки знаходяться за правилом буравчика і зображені в двох проекціях на рис. 9). Тоді модуль вектора В можна визначити по теоремі Піфагора:
де B1 і В2 визначаються по формулах розрахунку магнітної індукції для нескінченно довгого прямолінійного дроту зі струмом:
У нашому випадку r0=d/2. Тоді
Перевірка одиниць величин аналогічно виконаній в прикладі (3). Зробимо обчислення:
Приклад 6. Нескінченно довгий провід зігнутий так, як це зображено на рис. 10. Радіус R дуги кола дорівнює 10 см. Визначити магнітну індукцію В поля, створену в точці О струм І =80 А, що тече по цьому проводі. Рішення. Магнітну індукцію В в точці О знайдемо, використовуючи принцип суперпозиції магнітних полів:
Одним кінцем направлені в нескінченність, і дугу півкола (2) радіуса R. Тоді В=В1 + В2 + В3 де B1, B2 і В3 — магнітні індукції в точці О, створені струмом, що тече відповідно на першій, другій і третій ділянках проводу. Так як точка О лежить на осі дроту 1, то B 1=0 і тоді В=В2 + В3 З урахуванням того, що вектори В 2 і В 3 спрямовані відповідно до правила буравчика перпендикулярно площині креслення від нас, то геометричне підсумовування можна замінити алгебраїчним: В=В2 + В3 Магнітну індукцію В 2 знайдемо, скориставшись виразом для магнітної індукції в центрі колового струму:
У нашому випадку магнітне поле в точці О створюється лише половиною такого колового струму, тому
Магнітну індукцію В 3 знайдемо, скориставшись співвідношенням 3, виведеним у прикладі 1:
У нашому випадку r 0= R, a1=p/2(cosa1=0), a2 ®p (cosa2= -1 ), Тоді:
Використовуючи знайдені вирази для В 2 і В 3, одержимо
чи
Перевірка одиниць величин аналогічно виконана в прикладі 3. Зробимо обчислення:
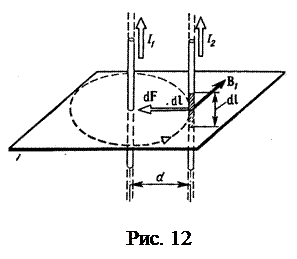
Приклад 7. По двом паралельним прямим проводах довжиною l =2,5 м кожний, що знаходяться на відстані d=20cм один від одного, течуть однакові струми І= 1кА. Обчислити силу взаємодії струмів. Рішення. Взаємодія двох проводів, по яких течуть струми, здійснюється через магнітне поле. Кожен струм створює магнітне поле, що діє на інший провід. Припустимо, що обидва струми (позначимо їх для зручності І 1 і І 2) течуть в одному напрямку. Струм І 1 створює в місці розташування другого дроту (зі струмом І 2) магнітне поле. Проведемо лінію магнітної індукції (пунктир на рис. 12) через другий провід і по дотичній до неї — вектор магнітної індукції В 1 Модуль магнітної індукції B1 визначається співвідношенням
Відповідно по закону Ампера, на кожен елемент другого дроту зі струмом І 2довжиною dl діє в магнітному полі сила
Тому що вектор dl перпендикулярний вектору B 1, то sin(dlB)=1 і тоді
Підставивши в цей вираз В 1 згідно (1), одержимо
Силу F взаємодії проводів зі струмом знайдемо інтегруванням:
Помітивши, що І 1 =І 2 =І
Переконаємося в тому, що права частина цієї рівності дає одиницю сили (Н):
Зробимо обчислення:
Сила F співпадає по напрямку із силою dF (рис. 12) і визначається (у даному випадку простіше) правилом лівої руки.
Приклад 8. Протон, що пройшов прискорюючу різницю потенціалів U =600В, влетів в однорідне магнітне поле з індукцією В =0,3Тл і почав рухатися по колу. Обчислити радіус R кола.(рис. 13) Рішення. Рух зарядженої частинки в однорідному магнітному полі буде відбуватися по колі тільки в тому випадку, коли частинка влетить у магнітне поле перпендикулярно лініям магнітної індукції υ ^B. Тому що сила Лоренца перпендикулярна вектору υ, то вона надасть частинці (протону) нормальне прискорення аn. Відповідно до другого закону Ньютона,
де m — маса протона. На рис.13 сполучена траєкторія протона з площиною креслення і надано (довільно) напрямок вектора υ. Силу Лоренца направимо перпендикулярно вектору u до центра кола (вектори аn і FЛ співпадає). Використовуючи правило лівої руки, визначимо напрямок магнітних силових ліній (напрямок вектора В). Перепишемо вираз (1) у скалярній формі (у проекції на радіус):
У скалярній формі FЛ=QВusina. У нашому випадку υ ^В і sina=l, тоді FЛ=QuВ. Тому що нормальне прискорення аn = v 2/ R, то вираз (2) перепишемо таким способом:
Звідси знаходимо радіус кола:
Помітивши, що mu є імпульс протона (р), цей вираз можна записати у вигляді
Імпульс протона знайдемо, скориставшись зв'язком між роботою сил електричного поля і зміною кінетичної енергії протона, тобто А=DТ, чи
де j1 - j2 — прискорююча різниця потенціалів (чи напруга, що прискорює, U); Т 1 і Т 2 — початкова і кінцева кінетичні енергії протона. Нехтуючи початковою кінетичною енергією протона (T 1» 0) і виразивши кінетичну енергію Т2 через імпульс р, одержимо
Знайдемо з цього виразу імпульс підставимо його у формулу (3):
чи
Переконаємося в тому, що права частина рівності дає одиницю довжини (м):
Підставимо у формулу (4) числові значення фізичних величин і зробимо обчислення:
Приклад 9. Електрон, влетівши в однорідне магнітне поле (В =0,2 Тл), став рухатися по кола радіуса R =5см. Визначити магнітний момент р m еквівалентного колового струму. Рішення. Електрон починає рухатися по кола, якщо він влітає в однорідне магнітне поле перпендикулярно лініям магнітної індукції. На рис.14 лінії магнітної індукції перпендикулярні площини креслення і спрямовані «від нас» (позначені хрестиками). Рух електрона по колу еквівалентно круговому струмі, який у даному випадку визначається виразом
де е - заряд електрона; Т – період його обертання. Період обертання можна виразити через швидкість електрона u і шлях, пройдений електроном за період Т=u/(2p R). Тоді
Знаючи І екв, знайдемо магнітний момент еквівалентного колового струму. По визначенню, магнітний момент контуру зі струмом виражається співвідношенням
де S — площа, обмежена колом, описаним електроном (S=p R 2). Підставивши І екв із (1) у виразу (2), одержимо
Скоротимо на p R і перепишемо цей вираз у вигляді:
В отриманому виразі є швидкість електрона, що зв'язана з радіусом R кола, по якій він рухається, співвідношенням
Переконаємося в тому, що права частина рівності дає одиницю магнітного моменту (А.м2):
Рішення. Електрон буде рухатися по гвинтовій лінії, якщо він влітає в однорідне магнітне поле під деяким кутом (a ¹ p/2 ) до ліній магнітної індукції. Розкладемо, як це показано на рис.15, швидкість v електрона на два складові: рівнобіжну вектори B(υ || ) і перпендикулярну йому (υ^). Швидкість υ| у магнітному полі не змінюється і забезпечує переміщення електрона уздовж силової лінії. Швидкість υ ^ у результаті дії сили Лоренца буде змінюватися тільки по напрямку (FЛ^ υ ^) (під час відсутності рівнобіжної складової (υ ||=0) рух електрона відбувався б по колу в площині, перпендикулярній магнітним силовим лініям). Таким чином, електрон буде брати участь одночасно в двох рухах: рівномірному переміщенні із швидкістю u|| і рівномірному русі по кола зі швидкістю u^. Період обертання електрона зв'язаний з перпендикулярною складовою швидкості співвідношенням
Знайдемо відношення
чи
де Скоротивши (2) на
Переконаємося в тому, що права частина рівності дає одиницю часу (с):
Зробимо обчислення:
Модуль швидкості З формули (2) виразимо перпендикулярну складову швидкості:
Рівнобіжну складову швидкості v || знайдемо з наступних розумінь. За час, рівний періоду звертання Т, електрон пройде уздовж силової лінії відстань, рівну кроку гвинтової лінії, тобто h = Tv ||, звідки
Підставивши замість Т праву частину виразу (2), одержимо
Таким чином, модуль швидкості електрона
Переконаємося в тому, що права частина рівності дає одиницю швидкості (м/с). Для цього помітимо, що R і h мають однакову одиницю — метр (м). Тому в квадратних дужках ми поставимо тільки одну з величин (наприклад, R): . Зробимо обчислення
Приклад 11. Альфа-частинка пройшла різницю потенціалів, що прискорює, U=104 В і влетіла в схрещені під прямим кутом електричне (Е=10кВ/м) і магнітне (В=0,1Тл) поля. Знайти відношення заряду альфа-частинки до її маси, якщо, рухаючи перпендикулярно обом полям, частка не випробує відхилень від прямолінійної траєкторії. Рішення. Для того щоб знайти відношення заряду Q альфа-частинки до її маси m, скористаємося зв'язком між роботою сил електричного поля і зміною кінетичної енергії частинки:
звідки Швидкість υ альфа-частинки знайдемо з наступних розумінь. У схрещених електричному і магнітному полях на заряджену частку, що рухається, діють дві сили: а) сила Лоренца б) Кулонівська сила В уздовж вісі Oz, швидкість υ — у позитивному напрямку вісі Ох, тоді FЛ і FК будуть спрямовані так, як показано на рисунку. Альфа-частинка не буде випробувати відхилення, якщо геометрична сума сил. FЛ=FК буде дорівнювати нулю. У проекції на вісь Оу одержимо наступну рівність (при цьому враховано, що u ^ В і sin a= 1): Тоді Звідки
Підставивши це вираз швидкості у формулу (1), одержимо
Переконаємося в тому, що права частина рівності дає одиницю питомого заряду (Кл/кг):
Зробимо обчислення:
Приклад 12. Коротка котушка, що містить N =103 витків, рівномірно обертається з частотою n =10с-1 навколо вісі АВ, що лежить у площині котушки і перпендикулярна лініям однорідного магнітного поля (В =0,04Тл). Визначити миттєве значення ЕРС індукції для тих моментів часу, коли площина котушки складає кут a=60° з лініями поля. Площа S котушки дорівнює 100 см2.
Зчеплення потоку
При обертанні котушки магнітний потік Ф, що пронизує котушку в момент часу t, змінюється за законом Ф = BS cosw t, де В — магнітна індукція; S — площа котушки; w — кутова швидкість котушки. Підставивши у формулу (2) вираз магнітного потоку Ф і продиференціювавши за часом, знайдемо миттєве значення ЕРС індукції:
Помітивши, що кутова швидкість w зв'язана з частотою обертання n котушки співвідношенням w=2p n і що кут wt=p/2 - a (рис. 17), одержимо (враховано, що sin (p/2 - a) =cos a)
Переконаємося в тому, що права частина цієї рівності дає одиницю ЕРС (В):
Зробимо обчислення:
Приклад 13. Квадратна дротова рамка зі стороною а =5 см і опором R =10 мОм знаходиться в однорідному магнітному полі (В =40 мТл). Нормаль до площини рамки складає кут a=30° з лініями магнітної індукції. Визначити заряд Q, що пройде по рамці, якщо магнітне поле виключити. Рішення. При вимиканні магнітного поля відбудеться зміна магнітного потоку. Внаслідок цього в рамці виникне ЕРС індукції, обумовлена основним законом електромагнітної індукції
ЕРС індукції викликає в рамці індукційний струм, миттєве значення якого можна визначити скориставшись законом Ома для повного ланцюга
Тому що миттєве значення сили індукційного струму
Проінтегрувавши вираз (1), знайдемо
Помітивши що при виключеному полі (кінцевий стан) Ф 2=0, остання рівність перепишеться у вигляді
Знайдемо магнітний потік Ф 1. По визначенню магнітного потоку маємо Ф 1= BScos a, де S — площа рамки. У нашому випадку (рамка квадратна) S = а 2. Тоді
Підставивши (3) у (2), одержимо | ||
|
| Поделиться: |





 ,
,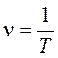
 називають фазою змінного струму.
називають фазою змінного струму.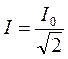
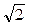 рази:
рази:
 ,
,





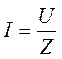



 називають коефіцієнтом трансформації. Якщо число витків вторинної обмотки більше, ніж первинної (N2> N1), то трансформатор називається підвищувальним. Якщо навпаки
називають коефіцієнтом трансформації. Якщо число витків вторинної обмотки більше, ніж первинної (N2> N1), то трансформатор називається підвищувальним. Якщо навпаки


 ,
, — спад напруги на вторинній обмотці.
— спад напруги на вторинній обмотці.

 Рішення. Для рішення задач скористаємося законом Біо - Савара-Лапласа і принципом суперпозиції магнітних полів. Закон Біо-Савара-Лапласа дозволяє визначити магнітну індукцію dВ, створювану елементом струму Іdl. Помітимо, що вектор dВ у точці А спрямований за площину креслення. Принцип суперпозиції дозволяє для визначення В скористатися геометричним підсумовуванням (інтегруванням):
Рішення. Для рішення задач скористаємося законом Біо - Савара-Лапласа і принципом суперпозиції магнітних полів. Закон Біо-Савара-Лапласа дозволяє визначити магнітну індукцію dВ, створювану елементом струму Іdl. Помітимо, що вектор dВ у точці А спрямований за площину креслення. Принцип суперпозиції дозволяє для визначення В скористатися геометричним підсумовуванням (інтегруванням): , (1)
, (1) ,
, ,
,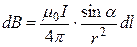 .
. . (2)
. (2) (рис. 2). Тоді підінтегральний вираз
(рис. 2). Тоді підінтегральний вираз  запишемо
запишемо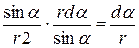 . Помітимо, що перемінна r також залежить від a, (r = r 0/sina); отже,
. Помітимо, що перемінна r також залежить від a, (r = r 0/sina); отже,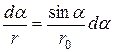 .
. ,
, , (3)
, (3) (4)
(4) .
. (5)
(5)
 , (1)
, (1) ;
; 
 за знак кореня, одержуємо
за знак кореня, одержуємо . (2)
. (2) ,
, ;
;  .
.

 ,
,


 з понять симетрії і що вектори dB ^ від різних елементів dl співнаправлені, замінимо векторне підсумовування (інтегрування) скалярним:
з понять симетрії і що вектори dB ^ від різних елементів dl співнаправлені, замінимо векторне підсумовування (інтегрування) скалярним: , де
, де  і
і 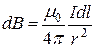 (оскільки dl перпендикулярний r і, отже, sina=1). Таким чином,
(оскільки dl перпендикулярний r і, отже, sina=1). Таким чином, .
. .
.
 .
.
 ,
, ,
,
 (провід довгий),
(провід довгий),  ( cosa2=cos(2p/3)=-1/2 ). Відстань
( cosa2=cos(2p/3)=-1/2 ). Відстань 
 .
. .
.
 Рішення. Відповідно до принципу суперпозиції магнітних полів магнітна індукція В поля, створеного струмами І 1 і І 2 визначається виразом В=B1 + В2, де B1 — магнітна індукція поля, створеного в точці А струмом І1;
Рішення. Відповідно до принципу суперпозиції магнітних полів магнітна індукція В поля, створеного струмами І 1 і І 2 визначається виразом В=B1 + В2, де B1 — магнітна індукція поля, створеного в точці А струмом І1; ,
, і
і 
 .
. .
. . У нашому випадку провід можна розбити на три частини (рис. 11): два прямолінійних проводи (1 і 3),
. У нашому випадку провід можна розбити на три частини (рис. 11): два прямолінійних проводи (1 і 3),
 .
. .
.
 .
.
 .
. .
. . (1)
. (1) .
. .
.
 .
. .
. .
.


 , (1)
, (1) . (2)
. (2)
 .
. . (3)
. (3) ,
,
 ,
, . (4)
. (4)
 .
.
 ,
, . (1)
. (1) , (2)
, (2)
 . (3)
. (3) , знайдемо швидкість
, знайдемо швидкість  і підставимо її у формулу (3):
і підставимо її у формулу (3): .
.
 Приклад 10. Електрон рухається в однорідному магнітному полі (В=10мТл) по гвинтовій лінії, радіус R якої дорівнює 1 см і крок h =6 см. Визначити період Т обертання електрона і його швидкість u.
Приклад 10. Електрон рухається в однорідному магнітному полі (В=10мТл) по гвинтовій лінії, радіус R якої дорівнює 1 см і крок h =6 см. Визначити період Т обертання електрона і його швидкість u. (1)
(1)
 . Для цього скористаємося тим, що сила Лоренца повідомляє електрону нормальне прискорення
. Для цього скористаємося тим, що сила Лоренца повідомляє електрону нормальне прискорення  . Відповідно до другого закону Ньютона можна написати
. Відповідно до другого закону Ньютона можна написати
 , (2)
, (2)
 , виразимо співвідношення
, виразимо співвідношення  . (
. ( ) і підставимо його у формулу (1):
) і підставимо його у формулу (1): .
.
 .
. , як це видно з рис. 15, можна виразити через
, як це видно з рис. 15, можна виразити через  |:
|: 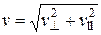
 .
.
 .
.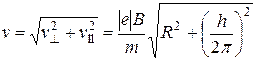 .
.
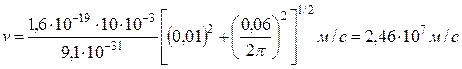 .
.

 (1)
(1) , спрямована перпендикулярно швидкості u і вектору магнітної індукції В;
, спрямована перпендикулярно швидкості u і вектору магнітної індукції В;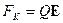 , співпадає за напрямком з вектором напруженості Е електростатичного поля (Q >0). На рис. 16 направимо вектор магнітної індукції
, співпадає за напрямком з вектором напруженості Е електростатичного поля (Q >0). На рис. 16 направимо вектор магнітної індукції ,
, .
. .
.

 Рішення. Миттєве значення ЕРС індукції ei визначається основним рівнянням електромагнітної індукції Фарадея—Максвела:
Рішення. Миттєве значення ЕРС індукції ei визначається основним рівнянням електромагнітної індукції Фарадея—Максвела: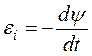 (1)
(1) , де N — число витків котушки, що пронизуються магнітним потоком Ф. Підставивши вираз Y у формулу (1), одержимо
, де N — число витків котушки, що пронизуються магнітним потоком Ф. Підставивши вираз Y у формулу (1), одержимо . (2)
. (2) .
. .
. .
. .
.
 , де R — опір рамки. Тоді
, де R — опір рамки. Тоді .
. , то це вираз можна переписати у вигляді
, то це вираз можна переписати у вигляді , звідки
, звідки  (1)
(1) чи
чи  .
. . (2)
. (2) . (3)
. (3)


