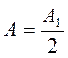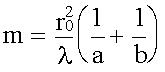Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Гюйгенса-Френеля. Метод зон Френеля.Содержание книги
Поиск на нашем сайте
Принцип Гюйгенса – любой волновой фронт – совокупность вторичных когерентных источников, к-ые действуют по направлению распространения света.
Принцип Гюйгенса-Френеля – волновое возмущение в некоторой точке можно рассматривать как результат интерференции волн, излучаемых вторичными источниками, расположенными на фронте.
Для решения данной задачи было предложено разбить фронт на зоны, т.ч. волны от соседних зон приходят в противофазе.
При таком построении волны, приходящие в N от соседних зон гасят др. др. Можно показать, что при таком построении площади зон одинаковы. Действие зоны уменьшается при увеличении её номера.
Действие всей открытой волновой пов-ти = половине действия центральной зоны. Вследствие интерференции в N свет идёт внутри узкого канала d<r первой зоны. Зонная пластинка – перекрывает все чёт либо нечёт зоны, в результате амплитуда в N резко возрастает.
+ - m нечёт, - - m чёт. +Am/2(нечёт) - - чёт
При нечёт m A в N совпадает с A1, при чёт = 0.
| |||||||
| ··22·· | ··23·· | ··24·· | ||||||
Дифракция от круглого отверстия к круглого диска. Дифракция - огибание волнами препятствий соизмеримыми с длиной волны. Под дифракцией волн понимают как нарушение законов геометрической оптики так их сопровождает интерфеционые явления. Любой волновой фронт можно представить как совокупность вторичных когерентных волн.An=(An-1+An+1)/2;Свет от (.)S распр. во все стороны, но вследствии из-за интерф в (.)N он идёт в узком канале диаметром<r1;(An-2/2-An-1+An/2)*An/2 -n нечётное;(An-3/2-An-2+An-1/2)+An-1/2+An –n чётное; Дифракция от круглого диска: Asinφ=(2n+1)λ/2 –max; Asinφ=2n(λ/2) –min; При небольших закрытой зоны An-A1~A;
Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r0. Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.
При нечетном числе зон в точке P будет максимум, так как колебания одной зоны останутся не погашенными.
Можно показать, что радиус зоны Френеля с номером m при не очень больших m: Расстояние "a" примерно равно расстоянию от источника до преграды, расстояние "b" - от преграды до точки наблюдения P.
Если отверстие оставляет открытым целое число зон Френеля, то, приравняв r0 и rm, получим формулу для подсчета числа открытых зон Френеля:
При m четном в точке P будет минимум интенсивности, при нечетном - максимум.
|
|
|||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.89.197 (0.009 с.) |

 →0
→0 →0
→0