
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные колебания механических систем. МаятникиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте

Пружинный маятник – груз массой m на абсолютно упругой пружине совершает колебания под действием упругой силы.
Таким образом М опережает по фазе смещение на
Математический маятник – это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешен точечный груз массой m, совершающий колебания под действием силы тяжести.
при малых углах
Гюйгенс
Физический маятник
Приведённая длина физ. маятника – длина такого мат. маятника, период колебаний к-ого совпадает с периодом колебаний данного физ. маятника. Th Штейнера:
Момент инерции J относ. произвольной оси равен моменту его инерции J0 относ. параллельной оси, проходящей через центр масс тела, сложенному с произведением массы тела m на квадрат расстояния l между осями.
Точка на прямой, соединяющей т. подвеса с центром инерции (масс) на расстоянии пр. длины от оси вращения, - центр качаний физ. маятника. Можно показать, что если подвесить физ. маятник в центре качаний, то пр. длина и T будут такими же, как и в начале.
|
Затухающие колебания
 Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Система называется линейной, если параметры, характеризующие существенные в рассматриваемом процессе физические свойства системы, не изменяются в ходе процесса.
В любой реальной колебательной системе существуют потери энергии, поэтому колебания будут уже не гармоническими, т.к. это не периодический процесс. Если потери небольшие, то можно приближённо ввести понятие периода затухающих колеб., к-ый будет несколько больше периода незатухающих колеб. Можно показать, что при малых энергетических потерях сила сопротивления прямо пропорциональна скорости:
где
При демпфировании система быстрее всего приходит в положение равновесия.
декремент затухания
логарифмический декремент Добротность Q прямо пропорц. числу колеб. за время, за к-ое амплитуда уменьшается в e раз (τ)
| ||||||||
| ··1·· | ··2·· | ··3·· |
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 688; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |



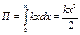

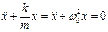

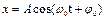


 . Ускорение и смещение находятся в противофазе.
. Ускорение и смещение находятся в противофазе.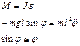




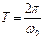 ,
, 
 ,
, 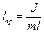



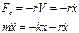



 ,
,
 =
=  - условие демпфирования,
- условие демпфирования,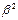 >
>  - апериодический процесс.
- апериодический процесс. ,
,  - время, через к-ое амплитуда колебаний уменьшается в e раз (время релаксации).
- время, через к-ое амплитуда колебаний уменьшается в e раз (время релаксации).







