
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонічні коливання і хвиліСодержание книги
Поиск на нашем сайте
С. Г. Авдєєв, Т. І. Бабюк О. С. Камінський ЗБІРНИК ЗАДАЧ З ФІЗИКИ Частина 2 (коливання і хвилі, хвильова і квантова оптика) Міністерство освіти і науки України Вінницький національний технічний університет С. Г. Авдєєв, Т. І. Бабюк О. С. Камінський ЗБІРНИК ЗАДАЧ З ФІЗИКИ Частина 2 (коливання і хвилі, хвильова і квантова оптика) Вінниця ВНТУ УДК 530(078) ББК 22.3я77 А18
Рекомендовано до друку Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України (протокол № 5 від 24.12.09 р.)
Рецензенти: І. О. Сівак, доктор технічних наук, професор О. В. Осадчук, доктор технічних наук, професор В. Г. Дзісь, кандидат фізико-математичних наук, доцент
Авдєєв, С. Г. А18Збірник задач з фізики. Ч. 2 (коливання і хвилі, хвильова і квантова оптика): навчальний посібник / С. Г. Авдєєв, Т. І. Бабюк, О. С. Камінський. – Вінниця: ВНТУ, 2010. – 122 с. Збірник задач складається з розділів “Механіка, електрика і електромагнетизм”, які традиційно викладаються в одному триместрі. Кожен окремий розділ супроводжується короткими теоретичними викладками і прикладами розв’язування задач. В першу чергу збірник задач призначений для організації та проведення практичних занять з курсу загальної фізики студентами вищих технічних навчальних закладів. Велика кількість і різноманітність задач, які ввійшли до збірника задач, дозволяє широко організовувати самостійну та індивідуальну роботу студентів. УДК 53(078) ББК 22.3я77 © С. Авдєєв, Т. Бабюк, О. Камінський, 2010 ЗМІСТ Частина 2
Гармонічні коливання і хвилі. Основні формули...................................... 3 Приклади розв’язування задач.................................................................. 8 Механічні хвилі. Основні формули.......................................................... 23 Приклади розв’язування задач................................................................. 27 Електромагнітні коливання і хвилі. Основні формули............................ 33 Приклади розв’язування задач................................................................. 36 Задачі.......................................................................................................... 39 Інтерференція світла. Основні формули................................................... 53 Приклади розв’язування задач................................................................. 61
Дифракція світла. Основні формули......................................................... 63 Поляризація світла. Основні формули..................................................... 67 Приклади розв’язування задач................................................................. 69 Дисперсія світла. Основні формули.......................................................... 73 Приклади розв’язування задач................................................................. 75 Теплове випромінювання. Основні формули........................................... 77 Приклади розв’язування задач................................................................. 78 Фотоефект. Основні формули................................................................... 82 Приклади розв’язування задач................................................................. 83 Тиск світла. Основні формули.................................................................. 85 Приклади розв’язування задач................................................................. 85 Ефект Компотна. Основні формули.......................................................... 86 Приклади розв’язування задач................................................................. 87 Задачі.......................................................................................................... 88 Література................................................................................................ 116 Додаток А................................................................................................. 117 Довідкові таблиці..................................................................................... 119
Частина 2 ГАРМОНІЧНІ КОЛИВАННЯ І ХВИЛІ Основні формули 1. Зміщення, швидкість і прискорення матеріальної точки при гармонічних коливаннях визначаються рівняннями:
х = А cos (w t + j0), υ = - A w sin (wt + j0), a = - A w2cos (wt + j0) = - w2 x,
де А – амплітуда коливань; w – циклічна частота; j0 – початкова фаза коливань. 2. Зв’язок циклічної частоти w з періодом коливань Т і частотою n:
w =
3. Сила, яка діє на тіло при вільних гармонічних коливаннях (квазіпружна сила):
F = ma = - m w2 x = - k x,
де k = mw2 – коефіцієнт квазіпружної сили, який вимірюється силою, що викликає зміщення х = 1. 4. Кінетична, потенціальна і повна енергії гармонічних коливань матеріальної точки:
5. Диференціальні рівняння малих коливань: а) математичний маятник
б) пружинний маятник
в) фізичний маятник
де І – момент інерції маятника відносно осі коливань; l – відстань від осі коливань до центра мас маятника;
При відсутності опору середовища циклічна частота коливань w називається власною циклічною частотою і позначається через w0. 6. При додаванні двох однаково направлених гармонічних коливань однакового періоду одержуємо гармонічне коливання того ж періоду, амплітуда якого А і початкова фаза j0 визначаються рівняннями:
tq j0 =
де А1 і А2 – амплітуди коливань, що складаються; j1 і j2 – початкові фази цих коливань. 7. При додаванні двох однаково направлених гармонічних коливань однакової амплітуди і близьких частот (w1 » w2) одержуємо биття, яке описується рівнянням:
x =
де
Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса, тому період биття дорівнює:
8. При додаванні двох взаємно перпендикулярних гармонічних коливань з однаковою частотою в напрямі координатних осей х і у матимемо рівняння траєкторії результуючого руху матеріальної точки:
де А1 і А2 – амплітуди коливань, що додаються; j2 - j1 – різниця фаз цих коливань. 9. Диференціальне рівняння згасаючих коливань:
або
де b = r – коефіцієнт опору середовища;
10. Загальний розв’язок диференціального рівняння для згасаючих коливань має вигляд: x = A0e-bt cos (wt + a),
де А0е-bt – амплітуда згасаючих коливань; w – циклічна частота згасаючих коливань. 11. Швидкість зменшення амплітуди згасаючих коливань характеризують логарифмічним декрементом згасання
δ= ln
де δ – логарифмічний декремент згасання; b – коефіцієнт згасання; Т – період згасаючих коливань. 12. Циклічна частота згасаючих коливань
w = 13. Період згасаючих коливань:
T = 14. Добротність коливальних систем
q = 2p
де Wt – повна енергія, яку має коливальна система на момент часу t; DW(t=T ) – втрати енергії коливальної системи за один період; δ – логарифмічний декремент згасання; b – коефіцієнт згасання; w0 – власна циклічна частота коливань; Т – період згасаючих коливань (при малих згасаннях Т» Т0).
15. Диференціальне рівняння вимушених коливань
або
де F0 – вимушувальна сила; w – циклічна частота вимушених коливань.
16. Загальний розв’язок диференціального рівняння вимушених коливань, які протягом певного часу встановлюються під дією вимушувальної сили має вигляд:
x = A cos (wt + a),
де А – амплітуда вимушених коливань; a – зсув за фазою вимушених коливань і вимушувальної сили. 17. Амплітуда вимушених коливань
A = де f0 = w0 – власна частота коливань системи; w – циклічна частота вимушувальної сили. 18. Зсув фази вимушених коливань:
tga = -
19. Резонансна частота і резонансна амплітуда:
wрез = Арез =
МЕХАНІЧНІ ХВИЛІ
Основні формули 1. Рівняння плоскої хвилі
де Ux,t – зміщення точок пружного середовища від положення рівноваги на відстані x від джерела; А – амплітудне зміщення цих точок;
l – довжина хвилі; w – циклічна частота коливань.
Рівняння сферичної хвилі
де r – радіус-вектор пружного середовища. 3. Зв’язок довжини хвилі з періодом коливань і частотою:
де υ – швидкість поширення хвиль в пружному середовищі;
Т – період коливань; n – частота коливань. 4. Швидкість поширення хвиль (фазова швидкість хвильового руху): а) поздовжня хвиля в твердому середовищі:
де Е – модуль Юнга; r – густина твердого середовища. б) поперечна хвиля в твердому середовищі:
де G – модуль зсуву; r – густина твердого середовища. в) повздовжня хвиля в рідкому середовищі:
де K – модуль об’ємної пружності рідини; r – густина рідини.
г) поздовжня хвиля в газоподібному середовищі:
5. Енергія пружних хвиль: а) кінетична енергія
де m = rSDx – маса виділеного елементу пружного середовища;
б) потенціальна енергія
в) повна енергія хвиль
г) середні значення повної енергії і густини енергії за час в один період
6. Потік енергії пружних хвиль R =
де
7. Вектор потоку енергії пружних хвиль
де
8. Ефект Допплера для звукових хвиль
де n – частота звуку джерела; с – швидкість поширення звукових хвиль в пружному середовищі; υ – швидкість руху приймача звуку; u – швидкість руху джерела звуку (нижній знак – джерело і приймач розходяться; верхній знак – джерело і приймач сходяться). 9. Інтерференція когерентних хвиль: а) максимуми інтерференції спостерігаються, коли
Dj = 2p де х2 - х1 – різниця ходу двох хвиль; Dj – різниця фаз хвиль; l – довжина хвилі; n = 0, 1, 2, 3,... – порядок max.
Або Dx = (x2 - x1) = n × l;
б) мінімуми інтерференції спостерігаються, коли:
Dj = 2p або D x = (x2 - x1) =
10. Рівняння стоячої хвилі
ux,t = де ux,t – зміщення точок середовища від положення рівноваги на відстані х від джерела коливань; А – амплітуда зміщення; k = w – циклічна частота коливань;
а) координати вузлів стоячої хвилі
kx =
де n = 0, 1, 2, 3,...; х – координати вузлів стоячої хвилі.
б) координати пучностей стоячої хвилі
kx =
де n = 0, 1, 2, 3,.... Основні формули 1. При вільних коливаннях в контурі, який складається з послідовно з’єднаних конденсатора ємністю С, котушки з індуктивністю L і резистора з омічним опором R, заряд на обкладках конденсатора змінюється за законом:
q = q0 e-bt × cos (wt + j0),
де q0 e-b t – амплітуда згасаючих коливань; b – коефіцієнт згасання; w – циклічна частота згасаючих коливань; q0 i j0 – початкові значення амплітуди заряду і фази коливань.
2. Циклічна частота згасаючих коливань:
w =
3. Власна циклічна частота коливального контуру:
4. Добротність коливального контуру:
або для малих значень R (наближена формула)
5. Якщо в коливальному контурі, який складається з конденсатора ємністю С, котушки резистора з омічним опором R, з’єднаних послідовно, діє періодично діюча е.р.с ξ = ξ0 cos wt, то в такому колі виникнуть вимушені коливання струму з частотою w
I = I0 cos (wt + j).
При цьому величини І0 і j виражаються формулами:
I0 =
tg j =
6. Амплітуда струму І0 досягне найбільшого значення (явище резонансу), якщо частота w вимушених коливань збіжиться з частотою w0 власних коливань: wp = w0 =
7. Швидкість поширення електромагнітних хвиль в прозорих середовищах:
υ = де e і m – діелектрична і магнітна проникності середовища; e0 і m0 – електрична і магнітна сталі вакууму. 8. Швидкість поширення електромагнітних хвиль в вакуумі:
c =
9. Показник заломлення середовища
10. Рівняння електромагнітних хвиль
Ez = E0 cos (wt - kx); Hу = H0 cos (wt - kx),
де Е0 і Н0 – амплітуди значень векторів напруженості електричного і магнітного полів в електромагнітній хвилі; k = 2p/l – хвильове число.
11. Густина енергії електромагнітних хвиль
w = we + wм =
де wе і wм – густина енергії відповідно електричного і магнітного полів електромагнітної хвилі.
12. Вектор густини потоку енергії електромагнітних хвиль, вектор Пойнтінга
де w – густина енергії поля;
Приклади роз’язування задач
Приклад 1. Коливальний контур має індуктивність 1,6 мГн, електричну ємність 0,04 мкФ і максимальну напругу Umax на клемах рівну 200 В. Визначити максимальну силу струму в контурі. Опором контуру знехтувати. Дано: L = 1,6 мГн C = 0,04 мкФ Umax = 200 В ____________ Іmax –? Розв’язування. Згідно з законом збереження енергії, максимальна енергія електричного поля конденсатора дорівнює максимальній енергії магнітного поля котушки індуктивності. Тому
Звідки Imax = Umax
Підставимо числові значення
Imax = 200 ×
Відповідь: Іmax = 1 А.
Приклад 2. Індуктивність коливального контуру дорівнює 0,5 мГн. Контур резонує на довжину хвилі 300 м. Визначити електроємність такого контуру. Опором контуру знехтувати. Дано: L = 0,5 мГн l = 300 м __________ С –? Розв’язування. Виразимо довжину електромагнітної хвилі через швидкість поширення і період коливань контуру
l = с Т, де с = 3 × 108 м/с – швидкість електромагнітних хвиль у вакуумі. Період коливань контуру дорівнює
Т = 2p
Тому
l = 2p с Звідки знаходимо ємність конденсатора
С =
Підставимо числові значення
С =
Відповідь: С = 51 пФ.
Приклад 3. В середовищі, для якого e = 4,00 і m = 1,00, поширюється плоска електромагнітна хвиля. Амплітуда електричного вектора хвилі Еmax = 200 В/м. На шляху хвилі розміщена поглинаюча поверхня, яка має форму диска радіусом r = 300 мм. Яку енергію поглинає ця поверхня за t = 1,00 хв? Період хвилі Т << t.
Дано: e = 4,00; m = 1,00 Еmax = 200 В/м r = 300 мм t = 1,00 хв _______________ W –? Розв’язування. Енергія, яка переноситься електромагнітною хвилею за одиницю часу через одиницю поверхні, перпендикулярно до напрямку поширення хвилі, визначається вектором Пойнтінга
де В електромагнітній хвилі вектори
Оскільки обидві величини Е і Н, які характеризують електромагнітну хвилю, в кожній її точці змінюються в часі за законом синуса або косинуса і знаходяться в однакових фазах, співвідношення (2) можна записати так:
R = E0 sin wt H0 sin wt = E0 H0 sin2 wt. (3)
Таким чином, величина R є функцією часу, а формули (2) і (3) дають лише миттєві значення цієї величини. Нехай через площадку S в напрямі перпендикулярному до напряму поширення хвилі переноситься за час t енергія W. Тоді густина потоку
R =
Через площадку S буде перенесена за час t енергія W, яка міститься в об’ємі циліндра з основою S і висотою υt, тобто
W = R S t. (5)
З урахуванням (3) маємо
W = E0 H0 S t sin2 wt. (6)
Згідно з теорією електромагнітних хвиль, густини енергії електричного і магнітного полів хвилі в будь-який момент часу однакові як для Е і Н, так і для Е0 і Н0. Тому
З формули (7) знаходимо Н0 і підставляємо в (6)
W =
Оскільки за умовою задачі Т << t, то величину sin2wt можна усереднити в часі, тобто
Остаточно одержуємо W = Підставимо числові значення W =
Відповідь: 1800 Дж.
Задачі
303. Точка виконує гармонічні коливання. Найбільше зміщення хmax дорівнює 10 см, найбільша швидкість υмах = 20 см/с. Знайти циклічну частоту ω коливань і максимальне прискорення amax. Відповідь: 2 с-1; 40 см/с2.
304. Точка виконує коливання за законом х = Asinωt. У деякий момент часу зміщення х1 точки виявилося рівним 5 см. Коли фаза коливань збільшилася вдвічі, зміщення х2 стало дорівнювати 8см. Знайти амплітуду А коливань. Відповідь:
305. Рівняння коливань точки має вигляд х = A cosω (t+ τ), де ω= πс -1; τ = 0,2 с. Визначити період Т і початкову фазу φ коливань. Відповідь: 2 с; 36о.
306. Точка виконує коливання за законом х = А cos (ωt+ φ), де А = 4 см. Визначити початкову фазу φ, якщо: а) Відповідь:;
307. Точка виконує коливання з амплітудою A = 4 см і періодом Т = 2 с. Написати рівняння цих коливань, вважаючи, що в момент часу t = 0 зміщення х(0) = 0 і υ(0)< 0. Визначити фазу (ωt + φ) для двох моментів часу: а) коли зміщення х = 1 см і υ > 0; б) коли швидкість υ = – 6 см/с і х < 0. Відповідь:
308. Точка виконує коливання за законом х = A cosωt, де А = 5 см; Відповідь:
309. Максимальна швидкість υmах точки, що виконує гармонічні коливання, дорівнює 10 см/с, максимальне прискорення amах = 100 см/с2. Знайти циклічну частоту ω коливань, їх період Т і амплітуду А. Написати рівняння коливань, прийнявши, що початкова фаза дорівнює нулю. Відповідь:
310. Коливання точки відбуваються за законом х = A cos (ωt + φ). У деякий момент часу зміщення х точки дорівнює 5 см, її швидкість υ = 20 см/с і прискорення a = – 80 см/с2. Знайти амплітуду А, циклічну частоту ω, період T коливань і фазу (ωt + φ) у розглянутий момент часу. Відповідь:
311. Точка бере участь у двох однаково направлених коливаннях х1 = А1 sin ωt і х2 = А2 cos ωt, де А1 = 1 см; А2 = 2 см; ω =1с-1. Визначити амплітуду А результуючого коливання, його частоту v і початкову фазу φ. Знайти рівняння цього руху. Відповідь: А = 2,24 см;
312. Матеріальна точка виконує гармонічні коливання уздовж осі х за законом: Відповідь: А = 6,0 см; Т = 2 с; х = 4,85 см; υ = 11,07 см/с; а = 47,6 см/с2.
313. Частинка виконує прямолінійні гармонічні коливання. Амплітуда швидкості частинки Відповідь: А = 6,28 см; ω = 3,5 с-1.
314. Матеріальна точка виконує коливання уздовж деякого напрямку за законом Відповідь: х1 = 0; х2 = 0,042м; х3 = 0,06 м; υ1 = 0,094 м/с; υ2 = 0,066 м/с; υ3 = 0; а1 = 0; а2 = 0,1 м/с2; а 3 = 0,15 м/с2.
315. Матеріальна точка виконує гармонічні коливання. Найбільше зміщення точки дорівнює 0,1 м, найбільша швидкість 0,2 м/с. Знайти циклічну частоту коливань і максимальне прискорення точки. Відповідь: ω = 2 с-1; амах. = 0,4м/с2.
316. Коливання матеріальної точки масою 0,1 г відбуваються за законом: Відповідь: Kмах = 4,9.10-6 Дж; Fмах = 1,97.10-4 Н.
317. До спіральної пружини підвісили тягарець, у результаті чого пружина розтяглася на 9 см. Який буде період коливань тягарця, якщо його трохи відтягнути від положення рівноваги, а потім відпустити? Відповідь: Т = 0,6 с.
318. Матеріальна точка виконує прямолінійні гармонічні коливання. Період коливань Т = 2 с, а амплітуда А = 4 см. Знайти швидкість Відповідь: υ = 0,108 м/с.
319. Матеріальна точка виконує прямолінійні гармонічні коливання. Циклічна частота ω = 4 c-1, амплітуда прискорення Відповідь: υ = 0,157 м/с.
320. Частинка виконує прямолінійні гармонічні коливання. При зміщенні частинки від положення рівноваги на x1 = 2,6 см її швидкість Відповідь: А = 0,0389 м; ω = 1 с-1.
321. Частинка одночасно бере участь у двох гармонічних коливаннях одного напрямку: x1 = 4cos4πt (см) і x2 = 3cоs(4πt + π/2) (см). Визначити циклічну частоту ω, амплітуду А і початкову фазу Відповідь: ω = 4π с-1; А = 0,05 м; φ = 36,86о.
322. Написати рівняння руху x(t) частинки, яка одночасно бере участь у двох гармонічних коливаннях одного напрямку: x1 = 30cosπt/3 і x2 = 30cos(πt/3 + π/6) мм. 323. Додаються два гармонічних коливання одного напрямку: x1 = 20cosωt (мм) і x2 = 20cos(ωt + π/3) (мм). Визначити амплітуду А і початкову фазу Відповідь: А=34,6 мм: φ = π/6.
324. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = sin
325. Частинка бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = 0,50sinωt і y = 1,5cosωt. Знайти рівняння руху частинки y(x). Побудувати графік результуючого траєкторії коливань і вказати на ній напрямок руху частинки.
326. Визначити амплітуду і початкову фазу результуючого коливання, утвореного при додаванні двох коливань однакового напрямку і періоду: x1 = 10sin3πt (см) і x2 = 12sin(3πt + Відповідь: А = 15,6 см; φ = 39,8о.
327. Зміщення освітленої точки на екрані осцилографа є результатом додавання двох взаємно перпендикулярних коливань, які описуються рівняннями: x = 1,5sin2πt см і y = 3sin2πt см. Написати рівняння результуючого коливання y(x) і побудувати його траєкторію.
327. Додаються два гармонічних коливання одного напрямку з однаковими періодами Т1 = Т2 = 1,5 с і амплітудами А1 = А2 = 2 см. Початкові фази коливань φ1 = π/2, φ2 = π/3. Визначити амплітуду А і початкову фазу Відповідь: А= 3,86 см; φ = 75о.
329. Точка рухається в площині x y за законом x = Asinωt і y = Bcosωt, де А = В = 10 см, Відповідь: а = 0,4 м/с2.
330. Матеріальна точка одночасно бере участь у двох взаємно перпендикулярних коливаннях, які виражаються рівняннями: x = 5cosπt см і y = 10cosπt см. Знайти рівняння траєкторії точки y(х) і швидкість точки в момент часу 1 с. Відповідь: υ = 0. 331. Частинка виконує прямолінійні згасаючі коливання з періодом Т = 4,5 с. Початкова амплітуда коливань Ao = 0,16 м, а амплітуда після 20 – ти повних коливань А = 0,01 м. Визначити коефіцієнт згасання β і логарифмічний декремент згасання Відповідь: β = 0,03 с-1; δ = 0,135.
332. Математичний маятник довжиною l = 1 м виконує згасаючі коливання в середовищі, логарифмічний декремент згасання якого Відповідь: δ2 |
|||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.170.61 (0.015 с.) |

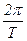 = 2 p n.
= 2 p n. ,
, ,
, .
. +
+  x = 0, де
x = 0, де  , звідки T = 2p
, звідки T = 2p  ;
; x = 0, де
x = 0, де  , звідки Т = 2p
, звідки Т = 2p  ;
; x = 0, де
x = 0, де  , звідки T = 2p
, звідки T = 2p  ,
, – зведена довжина.
– зведена довжина. ,
,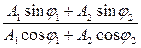 ,
, cos
cos  ,
,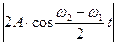 – амплітуда биття.
– амплітуда биття. Tб =
Tб =  , звідки Tб =
, звідки Tб = 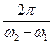 .
.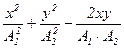 cos(j2 - j1) = sin2 (j2 - j1),
cos(j2 - j1) = sin2 (j2 - j1), 0
0
 – коефіцієнт згасання;
– коефіцієнт згасання; – власна циклічна частота коливань.
– власна циклічна частота коливань. ,
,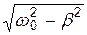 або w =
або w = 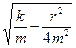 .
.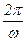 або Т =
або Т =  .
. або q =
або q =  ,
,
 ,
, ,
, ;
; .
. ;
; .
.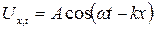 ,
, – хвильове число;
– хвильове число;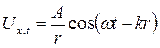 ,
,

 ,
,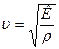 ,
, ,
, ,
,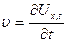 – швидкість хвильового руху точок середовища;
– швидкість хвильового руху точок середовища;



 ,
, – середнє значення повної енергії хвиль.
– середнє значення повної енергії хвиль. ,
, – середня густина енергії пружних хвиль;
– середня густина енергії пружних хвиль;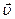 – вектор швидкості поширення хвиль в пружному середовищі.
– вектор швидкості поширення хвиль в пружному середовищі. n,
n, – частота звуку яка сприймається приймачем;
– частота звуку яка сприймається приймачем; ± 2n p,
± 2n p, .
. (2n + 1) l/2.
(2n + 1) l/2.
 – хвильове число;
– хвильове число; – амплітуда стоячої хвилі.
– амплітуда стоячої хвилі.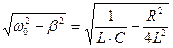
 .
.
 .
.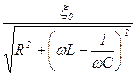 ;
; .
. .
. ,
, .
. .
. E H =
E H = 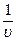 E H,
E H,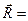

 і
і 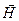 – вектори напруженості електричного і магнітного полів електромагнітної хвилі.
– вектори напруженості електричного і магнітного полів електромагнітної хвилі.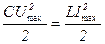 .
. .
. = 1 A.
= 1 A. .
. .
. .
. = 5,1 × 10-11 Ф.
= 5,1 × 10-11 Ф. , (1)
, (1) – вектор густини потоку енергії.
– вектор густини потоку енергії. . (2)
. (2) (4)
(4) . (7)
. (7) S t sin2 wt. (8)
S t sin2 wt. (8)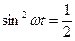 .
. .
. × 4 × 104 × 9 × 10-2 × 3,14 × 60 = 1800 Дж.
× 4 × 104 × 9 × 10-2 × 3,14 × 60 = 1800 Дж. .
. і
і  б)
б)  см і
см і  в) х(0) =
в) х(0) =  см і
см і 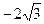 см і
см і 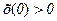 . Побудувати векторну діаграму для моменту часу t = 0.
. Побудувати векторну діаграму для моменту часу t = 0. ;
; 
 ;
;  .
. , де А = 4см,
, де А = 4см,  рад/с,
рад/с, 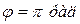 ;
; ;
;  .
. = 2 с-1. Визначити прискорення а точки в момент часу, коли її швидкість υ = 8 см/с.
= 2 с-1. Визначити прискорення а точки в момент часу, коли її швидкість υ = 8 см/с. .
. ; 0,628 с; 1 см;
; 0,628 с; 1 см;  .
.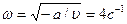 ;
;  ;
;  ;
; 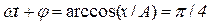 рад.
рад. ;
;  рад;
рад;  , де
, де  .
. , де t – час у секундах, х – у сантиметрах. Визначити амплітуду зміщення А и період коливань Т. Знайти зміщення х, швидкість
, де t – час у секундах, х – у сантиметрах. Визначити амплітуду зміщення А и період коливань Т. Знайти зміщення х, швидкість  і прискорення а матеріальна точки в момент часу t = 4,0 с.
і прискорення а матеріальна точки в момент часу t = 4,0 с. = 22 см/с, амплітуда її прискорення
= 22 см/с, амплітуда її прискорення  = 77 см/c². Визначити амплітуду зміщення А і циклічну частоту ω коливань частинки.
= 77 см/c². Визначити амплітуду зміщення А і циклічну частоту ω коливань частинки. , де ω = 1,57 c-1. Амплітуда швидкості
, де ω = 1,57 c-1. Амплітуда швидкості 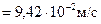 . Знайти для моментів часу
. Знайти для моментів часу 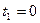 ,
,  ,
,  значення координати х, швидкості
значення координати х, швидкості 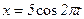 (см). Визначити максимальні значення кінетичної енергії і сили, яка повертає матеріальну точку до положення рівноваги.
(см). Визначити максимальні значення кінетичної енергії і сили, яка повертає матеріальну точку до положення рівноваги. результуючого коливання частинки. Побудувати векторну діаграму.
результуючого коливання частинки. Побудувати векторну діаграму. . Написати рівняння коливань частинки, прийнявши початкову фазу коливань
. Написати рівняння коливань частинки, прийнявши початкову фазу коливань  1 = 1,26. Визначити логарифмічний декремент згасання
1 = 1,26. Визначити логарифмічний декремент згасання 


