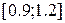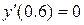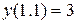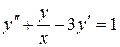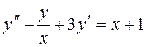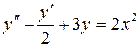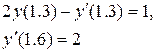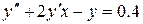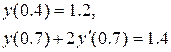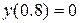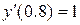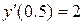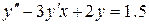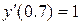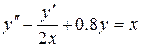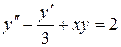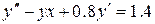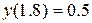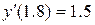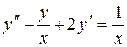Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язок систем диференціальних рівняньСодержание книги
Поиск на нашем сайте
Постановка задачі
Розглянемо систему
де Розв’язком (3.1) називається будь-яка сукупність функцій Загальний розв’язок системи
де Частинний розв’язок системи можна отримати із загального при певних значеннях довільних постійних, які можна знайти за наявності додаткових умов. Якщо ці умови задано в одній точці, отримаємо задачу Коші. Якщо для рівняння другого порядку додаткові умови задано в двох точках, отримаємо крайову задачу. Зауважимо, що диференціальне рівняння
зводиться до системи диференціальних рівнянь (3.1) заміною:
Тоді рівняння (3.2) зводиться до системи, що є частинним випадком системи (3.1):
а отже, розглянуті методи розв’язку систем рівнянь використовуються і для розв’язання диференціальних рівнянь вищих порядків.
Методи розв’язку задачі Коші
Метод Ейлера-Коші
Запишемо систему диференціальних рівнянь з початковими умовами (задача Коші) в загальному виді:
Початкові умови задамо в виді:
Формула Ейлера-Коші для задачі (3.4)-(3.5) має вид:
де
Модифікований метод Ейлера
Модифікований метод Ейлера розв’язку задачі (3.4)-(3.5) є однокроковим методом другого порядку, який реалізовано формулами:
де
Метод Ейлера-Коші з ітераціями
Метод Ейлера-Коші з ітераціями належить до неявних однокрокових методів і полягає в обчисленні на кожному кроці початкових значень:
Метод реалізовано за допомогою ітераційної формули:
де
де Зазвичай кількість ітерацій не має перевищувати 3-4, в противному випадку необхідно зменшити крок
Методи Рунге-Кута
Запишемо для задачі (3.4)-(3.5) формули методу Рунге-Кута 4 порядку:
де
Багатокрокові явні методи розв’язку
Широко розповсюдженим сімейством багатокрокових методів є методи Адамса. Відповідні формули розв’язку задачі (3.4)-(3.5) наведено нижче. Двокроковий метод:
Трикроковий метод:
Чотирикроковий метод:
П’ятикроковий метод:
Для того, щоб використати ці багатокрокові (
Крайова задача
Розглянемо звичайне диференціальне рівняння другого порядку:
Крайова задача полягає в пошуку розв’язку (значень функції)
або в загальному виді:
де Числові методи розв’язку крайової задачі можна розділити на дві групи: зведення розв’язку крайової задачі до послідовності розв’язків задач Коші (метод стрільби) та безпосереднє застосування кінцево-різницевого методу. Розглянемо метод кінцевих різностей, оскільки він дозволяє звести розв’язок крайової задачі для диференціального рівняння к розв’язку системи алгебраїчних рівнянь відносно значень функції, що шукається, на заданій множині точок. Це досягається шляхом заміни похідних, що входять в диференціальне рівняння, їх кінцево-різницевими апроксимаціями. Розіб’ємо відрізок Розв’язок крайової задачі замінимо обчисленням значень сіткової функції
Замінимо похідні, що входять до цих співвідношень їх кінцево-різницевими апроксимаціями:
Підставляючи ці вирази в (3.12), отримаємо систему різницевих рівнянь:
що є системою з Якщо крайові умови задані в загальному виді (3.11), то їх також необхідно представити в різницевому виді шляхом апроксимації похідних
Тобто граничні умови приймуть вид:
з яких легко знаходяться значення Отримана система (3.13), доповнена за необхідності рівняннями (3.14), є лінійною або нелінійною в залежності від того, лінійним чи нелінійним є вихідне диференціальне рівняння. Розглянемо детально лінійну крайову задачу:
де Побудуємо таку різницеву схему: – для внутрішніх вузлів
в результаті:
– для кінців відрізку інтегрування
Виконавши нескладні перетворення, отримаємо
Об’єднавши (3.15) та (3.16), отримаємо систему
розв’язуючи яку, знайдемо значення сіткової функції Отримана система (3.17) лінійних рівнянь є тридіагональною і може бути розв’язана методом прогонки. Для цього визначають коефіцієнти рівнянь виду:
де
Позначення
Потім виконується «зворотний хід»:
Завдання
Розв’язати диференціальне рівняння ІІ порядку на заданому відрізку для 1) задачі Коші. Номери методів розв’язку вказано в таблиці 3.1, відповідні методи – в таблиці 3.2. Початкові значення для методу Адамса розрахувати за методом Ейлера-Коші; 2) крайової задачі з початковими або граничними умовами відповідно. Прийняти, 3) Навести блок-схеми алгоритмів використаних методів. Таблиця 3.1 – Завдання на 3 частину курсової роботи
Таблиця 3.2 – Методи розв’язку задачі Коші
Перелік посилань
1. Демидович Б.П, Марон И.А. Основы вычислительной математики. 3-е изд., испр. – М.: Наука, 1966. – 664 стр. 2. Краскевич В.Е., Зеленский К.Х., Гречко В.И. Численные методы инженерных исследований. – Киев: Высшая шк., 1986. – 263 стр. 3. Боглаев Ю.П. Вычислительная математика и программирование – М.: Высш. шк., 1990. – 544 стр. 4. Копченова Н.В., Марон И.В. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 512с. 5. Самарский А.А., Гулин А.В. Численные методы: Учебное пособие для вузов. – М.: Наука. Гл. ред. физ-мат. лит., 1989. – 432 с. –C. 190 – 195. 6. Н.Н. Калиткин. Численные методы. Главная редакция физико-математической литературы "Наука", М., 1978. – C. 138 – 146. 7. Лященко М.Я., Головань М.С. Чисельні методи: Підручник. – К.: Либідь, 1996. – 288 с. C. 14-20, 26-45. 8. Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране. – М.: Изд-во МГУ, 1990. – 336 с. 9. Каханер Д., Моулер К., Нэш С. Численные методы и математическое обеспечение. – М.: Мир, 1998. – 575 с. 10. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986. – 288 с. 11. ДСТУ 3008-95. Документація. Звіти у сфері науки і техніки. Структура і правила оформлення. 12. ГОСТ 19.701-90 Единая система программной документации. Схемы алгоритмов, программ, данных и систем. Условные обозначения и правила выполнения.
ДОДАТОК
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.105 (0.007 с.) |

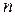 диференціальних рівнянь І-го порядку, розв’язаних відносно похідних:
диференціальних рівнянь І-го порядку, розв’язаних відносно похідних: (3.1)
(3.1) – незалежна змінна.
– незалежна змінна. , яка після підстановки в систему рівнянь (3.1), перетворює цю систему на тотожність.
, яка після підстановки в систему рівнянь (3.1), перетворює цю систему на тотожність. ,
, – довільні постійні.
– довільні постійні.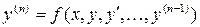 (3.2)
(3.2)
 (3.3)
(3.3)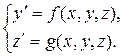 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) – крок приросту змінної
– крок приросту змінної 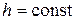 .
. (3.7)
(3.7)
 .
. (3.8)
(3.8) ,
,  ,
,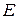 – задана точність.
– задана точність. , і повторити обчислення
, і повторити обчислення  з початку.
з початку.
 та
та




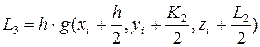


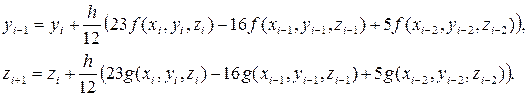

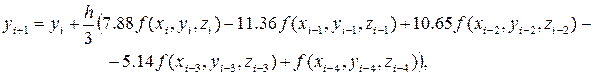

 -крокові) методи, необхідно спочатку будь-яким одно кроковим методом обчислити розв’язок на
-крокові) методи, необхідно спочатку будь-яким одно кроковим методом обчислити розв’язок на  попередніх кроках (в точках
попередніх кроках (в точках  ).
). (3.9)
(3.9) рівняння на відрізку
рівняння на відрізку  , що задовольняє на кінцях відрізка умовам, які задані в частинному виді:
, що задовольняє на кінцях відрізка умовам, які задані в частинному виді: , (3.10)
, (3.10) (3.11)
(3.11) – деякі постійні величини.
– деякі постійні величини. . Точки
. Точки  називають вузлами сітки,
називають вузлами сітки,  та
та  називають граничними вузлами, а
називають граничними вузлами, а  – внутрішніми вузлами.
– внутрішніми вузлами. в вузлових точках
в вузлових точках  . Для цього запишемо рівняння (3.9) для внутрішніх вузлів:
. Для цього запишемо рівняння (3.9) для внутрішніх вузлів: . (3.12)
. (3.12) ,
,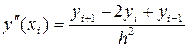 .
. ,
,  (3.13)
(3.13) алгебраїчного рівняння відносно значень сіткової функції
алгебраїчного рівняння відносно значень сіткової функції  . Значення
. Значення  та
та  , що входять до цієї системи, беруть з граничних умов.
, що входять до цієї системи, беруть з граничних умов. та
та  кінцево-різницевими співвідношеннями:
кінцево-різницевими співвідношеннями: ,
, .
. , (3.14)
, (3.14) ,
, ,
, та
та  – задані функції.
– задані функції. ,
, ,
, , (3.15)
, (3.15) :
:  ,
, 
 .
. (3.16)
(3.16)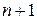 лінійних рівнянь:
лінійних рівнянь: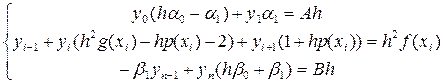 , (3.17)
, (3.17) .
. ,
,
 прийняті для
прийняті для  відповідно, що використовуються в системі (3.17). Потім знаходять елементи «прямого ходу»:
відповідно, що використовуються в системі (3.17). Потім знаходять елементи «прямого ходу»: ;
;  ;
; ;
;  ;
;  ;
; ,
,  .
. ,
,  .
.