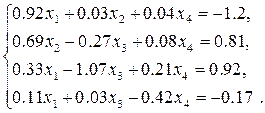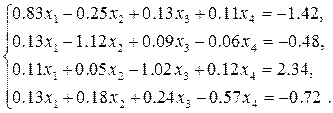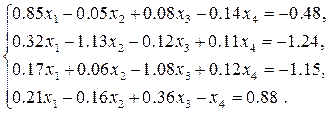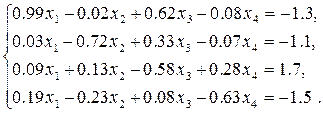Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка існування розв’язкуСодержание книги
Поиск на нашем сайте
Нехай
– це алгебраїчна сума
де Зазначимо, що зі зростанням Властивість 1. Значення визначника матриці не змінюється при транспонуванні цієї матриці. Властивість 2. Детермінант добутку двох матриць дорівнює добутку детермінантів цих матриць. Властивість 3. Якщо в детермінанті поміняти місцями два рядки (або два стовпці), то визначник змінить знак на протилежний. Властивість 4. Визначник з двома пропорційними рядками (стовпцями) дорівнює нулю. Властивість 5. Якщо всі елементи будь-якого рядка (стовпця) дорівнюють нулю, то визначник дорівнює нулю. Властивість 6. Якщо всі елементи будь-якого рядка (стовпця) мають загальний множник, то його можна винести за знак детермінанта. Властивість 7. Якщо кожен елемент будь-якого рядка (стовпця) є сумою двох доданків, то такий визначник дорівнює сумі двох визначників, в одному з них відповідний рядок (стовпчик) складається з перших доданків, а в іншому – з других доданків; інші рядки (стовпці) – такі ж як у вихідному детермінанті. Властивість 8. Визначник не змінює свого значення, якщо до всіх елементів будь-якого рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на одне й те ж число.
Метод зниження порядку
Полягає в обчисленні Мінором Алгебраїчним доповненням
Властивість 9. Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення.
Ця властивість називається розкладанням визначника по елементах рядка (стовпця). Використовуючи наведені властивості, можна зручно обчислювати визначники вищих порядків. Метод зниження порядку – добитися, щоб в деякому рядку (стовпці) стало якомога більше нулів, і розкласти визначник по елементах цього рідка (стовпця). Зрозуміло, що формула (1.4) значно спрощується, якщо всі крім одного елементи рядку або стовпця дорівнюють 0 (метод ефективного зниження порядку).
Метод Гауса за схемою Жордана
Властивість 10. Визначник верхньої трикутної, нижньої трикутної або діагональної матриці дорівнює добутку елементів, які стоять на головній діагоналі для верхньої трикутної: для нижньої трикутної: для діагональної: В методі Гауса за схемою Жордана необхідно привести визначник до діагонального виду (використовуючи властивості 3,6-8) і скористатися властивістю 10.
Прямі методи
Метод Крамера
Згідно даного методу кожне невідоме системи (1.1) представляється у виді відношення визначників. Запишемо його для системи рівнянь порядку
Тоді
де В методі Крамера необхідно обчислити (
Метод зворотної матриці
Якщо система рівнянь – невироджена, тобто визначник матриці системи За умови
або
Формула (1.5) дає розв’язок рівняння (1.3).
Метод Гауса
– За схемою одиничного ділення Метод заснований на приведенні матриці системи Зворотний хід методу Гауса полягає в послідовному обчисленні невідомих: розв’язуючи останнє рівняння, знаходимо єдине невідоме Розглянемо схему застосування методу Гауса для системи з трьох рівнянь:
Для виключення де
Помноживши друге рівняння системи (1.7) на де
Система (1.8) має трикутний вид. На цьому закінчується прямий хід методу Гауса. Зазначимо, що в процесі виключення невідомих, доводиться виконувати операції ділення на коефіцієнти Зворотний хід починається з рішення третього рівняння системи (1.8):
Використовуючи це значення, можна знайти
Аналогічно будується обчислювальний алгоритм для лінійної системи з довільним числом рівнянь.
– З вибором головного елементу Ця модифікація методу Гауса полягає в тому, що вимога нерівності 0 коефіцієнтів
– За схемою Жордана Також є модифікацією метода Гауса. В цьому випадку матриця системи Алгоритм розв’язку системи (1.1) методом Гауса-Жордана. 1. Нехай 2. Перевірити, чи відмінний діагональний елемент 3. Якщо відмінний, то 4. Для
де
аналогічно представимо нові праві частини рівнянь:
5. Збільшуємо
6. Обчислення вектора-розв’язку
– Метод прогонки Модифікація методу Гауса. Цей метод використовується для розв’язку частинного випадку розріджених систем лінійних рівнянь – рівнянь з тридіагональною матрицею. Такі системи виникають при числовому розв’язку крайових задач для диференціальних рівнянь. Запишемо систему рівнянь в виді:
де Метод прогонки складається з двох етапів – прямої прогонки (аналог прямого ходу методу Гауса) та зворотної прогонки (аналогу зворотного ходу методу Гауса). Пряма прогонка полягає в вираженні кожного невідомого
З першого рівняння
Оскільки З другого рівняння:
Так само Аналогічно можна обчислити прогоночні коефіцієнти для будь-якого
де Отже,
Далі виконується зворотна прогонка, для чого спочатку обчислюється
Потім
та формулами прогоночних коефіцієнтів. Під час обчислення
Числові методи
Метод уточнення коренів
Цей метод дозволяє уточнити розв’язок, отриманий за допомогою прямого методу. Метод уточнення коренів дає можливість зменшити помилки обчислень, а саме помилки округлення. Розглянемо систему лінійних рівнянь (1.1):
Нехай за допомогою будь-якого прямого методу (наприклад, методу Гауса), були обчислені наближені значення невідомих
Введемо позначення Віднімаючи з вихідної системи систему рівнянь з наближеними значеннями коренів, отримаємо таку систему:
Розв’язуючи цю систему знаходимо значення похибок
В той самий спосіб можна знайти поправки до розв’язку Зазначимо, що для знаходження певного значення похибок (поправок) розв’язуються системи лінійних рівнянь з тією самою матрицею
Метод простої ітерації
Проілюструємо цей метод на прикладі розв’язку системи:
Збіжність даного методу гарантується, якщо діагональні елементи
причому хоча б для одного рівняння нерівність має виконуватися строго. Зазначимо, що будь-які системи лінійних рівнянь можна звести до потрібного для збіжності виду за допомогою лінійних перетворень (додавання, вирахування, множення на константу) над рівняннями системи. Припустимо, що для даної системи умова збіжності виконується. Виразимо невідомі
Задамо деякі початкові (нульові) наближення значень невідомих. В якості нульових значень можуть бути обрані: стовпець вільних членів Підставляючи ці значення в праву частину рівнянь системи (1.10), одержуємо нове (перше) наближення для невідомих
Використовуючи обчислені значення
Ітераційний процес продовжується доти, поки значення
або критерієм по відносних відхиленнях (при
де Описаний алгоритм може бути розширений на систему з
Метод Зейделя
Ітераційний метод Зейделя відрізняється від методу простої ітерації тим, що на
Зазначені вище умова збіжності та умова припинення обчислень для методу простої ітерації залишаються вірними для методу Зейделя.
Завдання
Розв’язати систему лінійних рівнянь: 1) прямими методами (зворотної матриці, Крамера, Гауса) з двома знаками після коми; 2) уточнити отриманий в п. 1) розв’язок числовими методами (уточнення коренів, ітерацій або Зейделя) з точністю 3) Навести блок-схеми алгоритмів використаних методів.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.63.107 (0.008 с.) |

 – квадратна матриця порядку
– квадратна матриця порядку  , тоді визначник порядку
, тоді визначник порядку 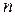

 добутків елементів матриці
добутків елементів матриці 
 ,
, – кількість інверсій переставлення
– кількість інверсій переставлення  .
. (
( доданки). На практиці для обчислення визначників вищих порядків застосовують методи, які використовують такі властивості визначників:
доданки). На практиці для обчислення визначників вищих порядків застосовують методи, які використовують такі властивості визначників: -го порядку.
-го порядку. елемента
елемента  визначника
визначника 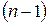 -го порядку, який утворюється з заданого визначника шляхом викреслювання
-го порядку, який утворюється з заданого визначника шляхом викреслювання  -го рядка та
-го рядка та  -го стовпця.
-го стовпця. елемента
елемента  визначника називається відповідний мінор
визначника називається відповідний мінор  , взятий з певним знаком
, взятий з певним знаком
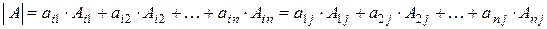 . (1.4)
. (1.4) ,
, ,
,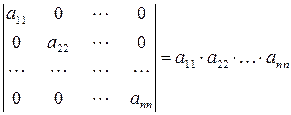 .
. :
: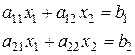
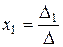 ,
,  ,
, ,
,  ,
,  .
.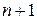 ) визначник
) визначник  , то система (1.1) або еквівалентне їй матричне рівняння (1.3), має єдиний розв’язок.
, то система (1.1) або еквівалентне їй матричне рівняння (1.3), має єдиний розв’язок. . Помноживши обидві частини рівняння (1.3) зліва на матрицю
. Помноживши обидві частини рівняння (1.3) зліва на матрицю 
 . (1.5)
. (1.5)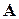 (1.2) до трикутного виду. Це досягається послідовним виключенням невідомих з рівнянь системи (1.1). Спочатку за допомогою першого рівняння виключається
(1.2) до трикутного виду. Це досягається послідовним виключенням невідомих з рівнянь системи (1.1). Спочатку за допомогою першого рівняння виключається  із усіх наступних рівнянь системи. Потім за допомогою другого рівняння перетвореної системи виключається
із усіх наступних рівнянь системи. Потім за допомогою другого рівняння перетвореної системи виключається  із третього і всіх наступних рівнянь. Цей процес, називаний прямим ходом методу Гауса, продовжується доти, поки в лівій частині останнього (
із третього і всіх наступних рівнянь. Цей процес, називаний прямим ходом методу Гауса, продовжується доти, поки в лівій частині останнього ( , тобто матриця системи буде приведена до трикутного виду.
, тобто матриця системи буде приведена до трикутного виду.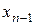 і т.д. Останнім знаходимо
і т.д. Останнім знаходимо  (1.6)
(1.6)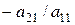 і
і  відповідно. Одержимо рівносильну систему виду:
відповідно. Одержимо рівносильну систему виду: , (1.7)
, (1.7) ,
, 
 ,
, 
 і додавши результат до третього рівняння, виключимо тим самим
і додавши результат до третього рівняння, виключимо тим самим  , (1.8)
, (1.8) ,
, .
. ,
,  і т.д. Тому вони мають бути відмінні від нуля. В іншому випадку необхідно відповідним чином переставити рівняння системи.
і т.д. Тому вони мають бути відмінні від нуля. В іншому випадку необхідно відповідним чином переставити рівняння системи. .
. ,
, .
. замінюється на більш жорстку: зі всіх елементів, що залишилися в
замінюється на більш жорстку: зі всіх елементів, що залишилися в  -му стовпці, необхідно обрати найбільший за модулем, і переставити рівняння системи так, що цей елемент став діагональним.
-му стовпці, необхідно обрати найбільший за модулем, і переставити рівняння системи так, що цей елемент став діагональним. .
.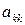 від
від  .
. , то необхідно замінити
, то необхідно замінити  -й (
-й ( ), в якій
), в якій 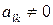 .
. обчислюємо нові матричні елементи, які позначимо, подібно попереднім, за правилом:
обчислюємо нові матричні елементи, які позначимо, подібно попереднім, за правилом: , якщо
, якщо  ,
,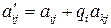 , якщо
, якщо 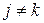 ,
, ;
; .
. , и переходимо до пункту 2. Це приведе до того, що всі елементи
, и переходимо до пункту 2. Це приведе до того, що всі елементи  .
. :
: .
.
 .
. через
через  за допомогою прогоночних коефіцієнтів:
за допомогою прогоночних коефіцієнтів: .
.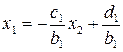 .
. , отже:
, отже: 
 .
. ,
, ,
, ,
, .
. :
: 
 , де
, де 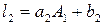 .
. .
.
 ,
, .
.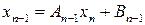 .
. з останнього рівняння:
з останнього рівняння: ,
, ,
, ,
, ,
, .
. за формулою
за формулою та
та  необхідно враховувати можливість ділення на 0. Щоб запобігти цьому бажано, щоб в таких системах виконувалась умова переважання діагональних елементів, тобто
необхідно враховувати можливість ділення на 0. Щоб запобігти цьому бажано, щоб в таких системах виконувалась умова переважання діагональних елементів, тобто 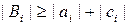 і хоча б для одного
і хоча б для одного 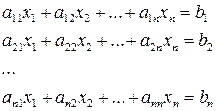 .
. . Підставивши ці розв’язки в ліві частини системи, отримаємо значення
. Підставивши ці розв’язки в ліві частини системи, отримаємо значення  , що відрізняються від
, що відрізняються від 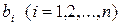 :
: .
. – похибка значень невідомих,
– похибка значень невідомих,  ,
,  .
.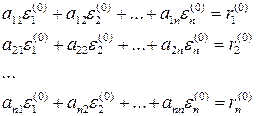 .
. (
(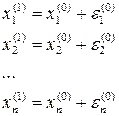 .
. (
( і т.д. Процес продовжується доти, поки всі чергові значення похибок (поправок)
і т.д. Процес продовжується доти, поки всі чергові значення похибок (поправок) 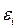 не стануть достатньо малими (такими, що задовольняють нас).
не стануть достатньо малими (такими, що задовольняють нас). не дорівнюють 0 і для них виконується умова:
не дорівнюють 0 і для них виконується умова: ,
, з першого, другого і третього рівнянь системи (1.9) відповідно:
з першого, другого і третього рівнянь системи (1.9) відповідно: . (1.10)
. (1.10) , відношення
, відношення  , а також будь-які інші значення (наприклад, нульові), тому що виконання умови збіжності забезпечує досягнення результату при будь-яких початкових умовах.
, а також будь-які інші значення (наприклад, нульові), тому що виконання умови збіжності забезпечує досягнення результату при будь-яких початкових умовах. . (1.11)
. (1.11) ,
,  ,
,  , можна тим саме способом провести другу ітерацію, у результаті якої будуть знайдені другі наближення до розв’язку
, можна тим саме способом провести другу ітерацію, у результаті якої будуть знайдені другі наближення до розв’язку  ,
,  ,
,  . Наближення з номером
. Наближення з номером  можна представити у виді:
можна представити у виді: . (1.12)
. (1.12) ,
,  ,
,  , не стануть близькими з заданою похибкою до значень
, не стануть близькими з заданою похибкою до значень  ,
,  ,
, 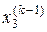 , що можна перевірити критерієм по абсолютних відхиленнях
, що можна перевірити критерієм по абсолютних відхиленнях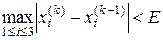 , (1.13)
, (1.13) )
)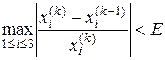 , (1.14)
, (1.14)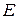 – задана похибка невідомих. При виконанні умови (1.13) або (1.14) процес ітерацій припиняється і за шукані розв’язки приймаються їх останні обчислені значення.
– задана похибка невідомих. При виконанні умови (1.13) або (1.14) процес ітерацій припиняється і за шукані розв’язки приймаються їх останні обчислені значення. використовуються значення
використовуються значення  ,
,  , обчислені на тій самій ітерації. Наближення на
, обчислені на тій самій ітерації. Наближення на  , (1.15)
, (1.15) ;
;