Паралельні векторні системи (PVP)

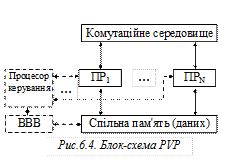
Блок - схема PVP наведена на рис.6.4, характеристики – в табл.6.4.

Таблиця 6.4. Характеристики PVP

Архітектура	Основна ознака - наявність спеціальних векторно – конвеєрних процесорів, у яких передбачені команди однотипної обробки векторів незалежних даних, що ефективно виконуються на конвеєрних функціональних пристроях. Як правило, кілька таких процесорів (1 - 16) працюють одночасно над спільною пам'яттю (аналогічно SMP) у рамках багатопроцесорних конфігурацій. Кілька таких вузлів можуть бути об'єднані за допомогою комутатора (аналогічно MPP).
Приклади	NEC SX - 4/SX - 5, лінія векторно - конвеєрних комп'ютерів CRAY: CRAY - 1, CRAY J90/T90, CRAY SV1, серія Fujitsu VPP.
Модель програмування	Ефективне програмування має на увазі векторизацію циклів (для досягнення розумної продуктивності одного процесора) і їх розпаралелення (для одночасного завантаження декількох процесорів однією задачею).

Перевагами PVP є висока швидкодія і практично відсутність проблеми взаємодії між процесорами; недоліком – висока вартість.

 

Кластерні системи

Характеристики кластерної системи наведені в табл.6.5.

Таблиця 6.5. Характеристики кластерних систем

Архітектура	Набір робочих станцій (чи ПК) загального призначення, використовується як дешевий варіант масивно – паралельного комп'ютера. Для зв'язку вузлів використовується одна з стандартних мережних технологій (Fast/ Gigabit Ethernet, Myrinet) на базі шинної чи архітектури комутатора. При об'єднанні в кластер комп'ютерів різної потужності чи різної архітектури, говорять про гетерогенні (неоднорідні) кластери. Вузли кластера можуть одночасно використовуватися як користувацькі робочі станції.
Приклади	NT - кластер у NCSA, Beowulf - кластери.
Операційна система	Використовуються стандартні для робочих станцій ОС, найчастіше, вільно розповсюджувані - Linux/FreeBSD, разом зі спеціальними засобами підтримки паралельного програмування і розподілу навантаження.
Модель програмування	Програмування, як правило, у рамках моделі передачі повідомлень (найчастіше - MPI). Дешевизна подібних систем обертається великими накладними витратами на взаємодію паралельних процесів між собою, що сильно звужує потенційний клас розв'язуваних задач.

Вправи і завдання до теми №6

1. Є дві системи. Одна має швидкі процесори і повільні канали зв’язку, а інша – повільні процесори і швидкі канали зв’язку. Які переваги і недоліки кожної системи? На якій системі програми будуть мати кращу масштабованість?

2. Наведіть приклад реальної обчислювальної системи з розподіленою пам’яттю і комутаційною мережею, що має топологію двовимірного тора.

3. Допустимо, що перемножуються дві квадратні матриці. Які появляться особливості в організації обчислювальних процесів, якщо взяти матриці максимального розміру і старатися розв’язати задачу максимально швидко? Розгляньте варіанти обчислювальних процесів:

а) з спільною пам’яттю і універсальними процесорами;

б) з спільною пам’яттю і конвеєрними суматорами, перемножувачами і пристроями ділення;

в) з розподіленою пам’яттю і універсальними процесорами;

г) з розподіленою пам’яттю і конвеєрними суматорами, перемножувачами і пристроями ділення.

 

Тема №7: Схеми паралельних алгоритмів задач.

Питання:

Схеми алгоритмів задач

2. Алгоритми перемноження матриці на матрицю і їх реалізація на структурах типу: кільцева, 2D (решітка), 3D (куб)

Вправи і завдання до теми №7

 

Схеми алгоритмів задач

Паралельні алгоритми використовуються для розв’язання таких задач: множення матриці на матрицю, задача Діріхле, розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) методом Гауса і методом простої ітерації та інші. В простому варіанті сіткової задачі (задача Діріхле) крок сітки в просторі обчислень однаковий і не змінюється в процесі обчислень. При динамічній зміні кроку сітки треба було б розв’язувати задачу паралельного програмування, як перебалансування обчислювального простору між комп'ютерами, для вирівнювання обчислювального навантаження комп'ютерів.

Особливості алгоритмів:

1. Задачі відносяться до задач, що розпаралелюються грубозернистими методами.

2. Для представлення алгоритмів використовується SPMD-модель обчислень (розпаралелення за даними).

3. Однорідне розподілення даних по комп'ютерах - основа для гарного балансу часу обчислення і часу, затрачуваного на взаємодії віток паралельної програми. Такий розподіл використовується з метою забезпечення рівності обсягів частин даних, що розподіляються, і відповідності нумерації частин даних, що розподіляються, нумерації комп'ютерів у системі.

4. Вихідними даними розглянутих алгоритмів є матриці, вектори і 2D (двовимірний) простір обчислень.

5 У розглянутих алгоритмах застосовуються такі способи однорідного розподілу даних: горизонтальними смугами, вертикальними смугами і циклічними горизонтальними смугами.

При розподілі горизонтальними смугами матриця, вектор або 2D простір "розрізається" на смуги по рядках. Нехай M - кількість рядків матриці, кількість елементів вектора або кількість рядків вузлів 2D простору, P - кількість віртуальних комп'ютерів у системі, С1 = М / Р - ціла частина від ділення, С2 = М /Р - дробова частина від ділення. Дані розрізаються на Р смуг. Перші (Р-С2) смуг мають по С1 рядків, а інші С2 смуги мають по С1+1 рядків.

Смуги даних розподіляються по комп'ютерах таким чином. Перша смуга поміщається в комп'ютер з номером 0, друга смуга - у комп'ютер 1, і т.д. Такий розподіл смуг по комп'ютерах враховується в паралельному алгоритмі. Розподіл вертикальними смугами аналогічний попередньому, тільки в розподілі беруть участь стовпці матриці або стовпці вузлів 2 D простору. При розподілі циклічними горизонтальними смугами дані розрізаються на кількість смуг значно більшу, від кількості комп'ютерів. І найчастіше смуга складається з одного рядка. Перша смуга завантажується в комп'ютер 0, друга - у комп'ютер 1, і т.д., потім, Р-1-а смуга знову в комп'ютер 0, Р-а смуга в комп'ютер 1, і т.д.

Проте, тільки однорідність розподілу даних ще недостатня для ефективного виконання алгоритму. Ефективність алгоритмів залежить і від способу розподілу даних. Різний спосіб представлення даних веде, відповідно, і до різної організації алгоритмів, що обробляють ці дані.

Точні значення ефективності конкретного паралельного алгоритму можуть бути визначені на конкретній обчислювальній системі на деякому наборі даних. Тобто, ефективність паралельних алгоритмів залежить, по-перше, від обчислювальної системи, на якій виконується задача, а, по-друге, від структури самих алгоритмів. Вона визначається як відношення часу реалізації паралельного алгоритму задачі до часу реалізації послідовного алгоритму цієї ж задачі. Ефективність можна вимірювати і співвідношенням між часом, витраченим на обмін даними між процесами, і загальним часом обчислень. Зауважимо, що ефективність алгоритмів, що використовують глобальний обмін даними, знижується з збільшенням кількості паралельних віток. Тобто з збільшенням кількості комп'ютерів у системі, швидкість виконання глобальної операції обміну буде падати. До таких задач можна віднести, наприклад, задачу розв’язання СЛАР ітераційними методами. Ефективність алгоритмів, у яких обмін даними здійснюється тільки локально, буде незмінною з збільшенням кількості паралельних віток.

 

2. Алгоритми перемноження матриці на матрицю і їх реалізація на структурах типу: кільцева, 2D (решітка), 3D (куб)

Множення матриці на вектор і матриці на матрицю є базовими макроопераціями для багатьох задач лінійної алгебри, наприклад ітераційних методів розв’язання систем лінійних рівнянь і т.п. Тому приведені алгоритми тут можна розглядати як фрагменти в алгоритмах цих методів. Розглянемо три алгоритми множення матриці на матрицю. Розмаїтість варіантів алгоритмів виникає із-за розмаїтості обчислювальних систем і розмаїтості розмірів задач. Розглядаються і різні варіанти завантаження даних у систему: завантаження даних через один комп'ютер; і завантаження даних безпосередньо кожним комп'ютером з дискової пам'яті. Якщо завантаження даних здійснюється через один комп'ютер, то дані зчитуються цим комп'ютером з дискової пам'яті, розрізаються на частини, які розсилаються іншим комп'ютерам. Але дані можуть бути підготовлені і заздалегідь, тобто заздалегідь розрізані вроздріб і кожна частина записана на диск у виді окремого файлу зі своїм ім'ям; потім кожен комп'ютер безпосередньо зчитує з диска, призначений для нього файл.

Алгоритм 1- Перемноження матриці на матрицю на кільцевій структурі

Задано дві вихідні матриці A і B. Обчислюється добуток C = А х B, де А - матриця n₁ х n₂, і B - матриця n₂ х n₃. Матриця результатів C має розмір n₁ х n₃. Вихідні матриці попередньо розрізані на смуги, смуги записані на дискову пам'ять окремими файлами зі своїми іменами і доступні всім комп'ютерам. Матриця результатів повертається в нульовий процес.

Реалізація алгоритму виконується на кільці з p₁ комп'ютерів. Матриці розрізані як показане на рис. 7.1: матриця А розрізана на p₁ горизонтальних смуг, матриця B розрізана на p₁ вертикальних смуг, і матриця результату C розрізана на p₁ смуги. Тут передбачається, що в пам'ять кожного комп'ютера завантажується і може знаходитися тільки одна смуга матриці А і одна смуга матриці B.

Рис. 7.1 Розрізування даних для паралельного алгоритму добутку двох матриць при обчисленні на кільці комп'ютерів. Виділені смуги розташовані в одному комп'ютері.

 

Оскільки за умовою в комп'ютерах знаходиться по одній смузі матриць, то смуги матриці B (або смуги матриці A) необхідно "прокрутити" по кільцю комп'ютерів повз смуги матриці A (матриці B). Кожний зсув смуг уздовж кільця і відповідна операція множення наведена на рис.7.2 у виді окремого кроку. На кожному з таких кроків обчислюється тільки частина смуги. Процес i обчислює на j-м кроці добуток i-й горизонтальної смуги матриці A j-ї вертикальної смуги матриці B, добуток отриманий у підматриці(i,j) матриці C.

Обчислення відбувається в такій послідовності.

1. Кожен комп'ютер зчитує з дискової пам’яті відповідну йому смугу матриці А. Нульова смуга повинна зчитуватися нульовим комп'ютером, перша смуга - першим комп'ютером і т.д., остання смуга - зчитується останнім комп'ютером. На рис. 7.2 смуги матриці А і B пронумеровані.

2. Кожен комп'ютер зчитує з дискової пам’яті відповідну йому смугу матриці B. У даному випадку нульова смуга повинна зчитуватися нульовим комп'ютером, перша смуга - першим комп'ютером і т.д., остання смуга - зчитується останнім комп'ютером.

3. Обчислювальний крок 1. Кожен процес обчислює одну підматрицю добутку. Вертикальні смуги матриці B зсуваються уздовж кільця комп'ютерів.

4. Обчислювальний крок 2. Кожен процес обчислює одну підматрицю добутку. Вертикальні смуги матриці B зсуваються уздовж кільця комп'ютерів. І т.д.

5. Обчислювальний крок p1-1. Кожен процес обчислює одну підматрицю добутку. Вертикальні смуги матриці B зсуваються уздовж кільця комп'ютерів.

6. Обчислювальний крок p1. Кожен процес обчислює одну підматрицю добутку. Вертикальні смуги матриці B зсуваються уздовж кільця комп'ютерів.

7. Матриця C збирається в нульовому комп'ютері.

1. scatter A 2. scatter B

7. Збір результатів у С

Рис. 7.2 Стадії обчислень добутку матриць у кільці комп'ютерів.

Якщо "прокручувати" вертикальні смуги матриці B, то матриця С буде розподілена горизонтальними смугами, а якщо "прокручувати" горизонтальні смуги матриці A, то матриця С буде розподілена вертикальними смугами.

Алгоритм характерний тим, що після кожного кроку обчислень здійснюється обмін даними. Нехай t_u, t_s, і t_p час операцій, відповідно, множення, додавання і пересилання одного числа в сусідній комп'ютер. Тоді сумарний час операцій множень дорівнює:

U = (n₁*n₂)*(n₃*n₂)*t_u,

сумарний час операцій додавань дорівнює:

S = (n₁*n₂)*(n₃*(n₂-1))*t_s,

сумарний час операцій пересилань даних по всіх комп'ютерах дорівнює:

P = (n₃*n₂)*(p₁-1)*t_p.

Загальний час обчислень визначимо як:

T = (U+S+P)/p₁

Відношення часу "обчислень без обмінів" до загального часу обчислень є величина:

K = (U+S)/(U+S+P).

Якщо час передачі даних великий в порівнянні з часом обчислень, або канали передачі повільні, то ефективність алгоритму буде не висока. Тут не враховується час початкового завантаження і вивантаження даних у пам'ять системи. У смугах матриць може бути різна кількість рядків, а різниця в кількості рядків між смугами - 1. При великих матрицях цим можна знехтувати.

При достатніх ресурсах пам'яті в системі краще використовувати алгоритм, у якому мінімізовані обміни між комп'ютерами в процесі обчислень. Це досягається за рахунок дублювання деяких даних у пам'яті комп'ютерів. У наступних двох алгоритмах використовується цей підхід.

Алгоритм 2 - Перемноження матриці на матрицю на2D решітці

Обчислюється добуток C = А х B, де А - матриця n₁ х n₂, і B - матриця n₂ х n₃. Матриця результатів C має розмір n₁ х n₃. Вихідні матриці спочатку доступні на нульовому процесі, і матриця результатів повертається в нульовий процес.

Паралельне виконання алгоритму здійснюється на двовимірній (2D) решітці комп'ютерів розміром p₁ х p₂. Матриці розрізані, як показано на рис. 7.3: матриця А розрізана на p₁ горизонтальних смуг, матриця B розрізана на p₂ вертикальних смуг, і матриця результату C розрізана на p₁ х p₂ підматриці (або субматриці).

A B C

Рис. 7.3 Розрізування даних для паралельного алгоритму добутку двох матриць при обчисленні на 2D решітці комп'ютерів. Виділені дані розташовані в одному комп'ютері.

Кожен комп'ютер (i,j) обчислює добуток i -й горизонтальної смуги матриці A і j -й вертикальної смуги матриці B, добуток отримується у підматриці (i,j) матриці C.

Послідовність стадій обчислення наведена на рис.7.4:

1. Матриця А розподіляється по горизонтальних смугах уздовж координати (x,0).

2. Матриця B розподіляється по вертикальних смугах уздовж координати (0,y).

3. Смуги А поширюються у вимірі y.

4. Смуги B поширюються у вимірі х.

5. Кожен процес обчислює одну підматрицю добутку.

7. Матриця C збирається з (x,y) площини.

Здійснювати пересилання між комп'ютерами під час обчислень не потрібно, тому що всі смуги матриці А перетинаються з усіма смугами матриці B у пам'яті комп'ютерів системи.

Цей алгоритм ефективніший від попереднього, тому що непродуктивний час пересилань даних здійснюється тільки при завантаженні даних у пам'ять комп'ютерів і при їхньому вивантаженні, і обміни даними в процесі обчислень відсутні. Оскільки час обмінів рівний нулеві, а час завантаження і вивантаження тут не враховується, то загальний час обчислень дорівнює:

T = (U+S)/(p₁*p₂)

А відношення часу "обчислень без обмінів" до загального часу обчислень є величина:

K = (U+S)/(U+S)=1.

 

2.scatter B координати

3. broadcast підматриць A

4. broadcast 5. обчислення
підматриць B добутків
(підматриць в C )

6. збір
результатів в C

Рис. 7.4 Стадії обчислення добутку матриць у 2D паралельному алгоритмі.

Алгоритм 3 - Перемноження матриці на просторовій сітці комп’ютерів

Для великих матриць, час обчислення добутків може бути зменшений шляхом застосуванням алгоритму, що здійснює обчислення на 3-мірній (просторовій) сітці комп'ютерів.

У приведеному нижче алгоритмі відображаються основні дані обсягом n₁ х n₂ + n₂ х n₃ + n₁ х n₃ на об'ємну сітку комп'ютерів розміром p₁ х p₂ х p₃. Матриці розрізані, як показано на рис. 7.5: Матриця А розрізана на p₁ х p₂ субматриці, матриця B розрізана на p₂ х p₃ субматриці, і матриця C розрізана на p₁ х p₃ субматриці. Комп'ютер (i,j,k) обчислює добуток субматриці (i,j) матриці А і субматриці (j,k) матриці B. Субматриця (i,k) матриці C виходить підсумовуванням проміжних результатів, обчислених у комп'ютерах (i,j,k), j = 0,...,p2-1.

Послідовність стадій обчислення наведена на рис. 7.6.

1. Субматриці А розподіляються в (x,y,0) площині.

2. Субматриці B розподіляються в (0,y,z) площині.

3. Субматриці А поширюються у вимірі z.

4. Субматриці B поширюються у вимірі х.

5. Кожен процес обчислює одну субматрицю.

6. Проміжні результати редукується у вимірі y.

7. Матриця C збирається з (x,0,z) площини.

Алгоритм подібний до попереднього, але додатково розрізаються ще смуги матриць, і ці розрізані смуги розподіляються в третьому вимірі y. У даному випадку в кожному комп'ютері будуть перемножуватися тільки частини векторів рядків матриці А і частини стовпців матриці B. В результаті буде тільки часткова сума для кожного елемента результуючої матриці C. Операція підсумовування уздовж координати y цих отриманих часткових сум для результуючих елементів і завершує обчислення матриці C.

Загальний час обчислень у цьому алгоритмі дорівнює:

T = (U+S)/(p₁*p₂*p₃)

А відношення часу "обчислень без обмінів" до загального часу обчислень є величина:

K = (U+S)/(U+S)=1.

A B C

Рис. 7.5 Розрізування даних для паралельного алгоритму добутку двох матриць при обчисленні на просторовій сітці комп'ютерів.

2. scatter B 3. broadcast
підматриць з А

4. broadcast підматриць зУ 5. Обчислення добутків підматриць у С)

6. reduce (підсумовування)добутків 7. gather C (збір результатів)

Рис. 7.6. Стадії обчислень у 3D паралельному алгоритмі добутку матриць.