Приклади реалізації мереж Петрі

В принципі кожну програму, написану на будь-якій мові програмування, можна представити у формі розширеної мережі Петрі. При цьому треба мати на увазі, що "пам'ять маркувань" деякого вузла може містити тільки додатне число або нуль. Від’ємні числа можуть, наприклад, представлятися додатковим вузлом, що визначає знаки чисел. Кожна наведена тут мережа має спеціальний "стартовий" вузол, з якого починається обчислення, i вузол "готовності", який маркується тоді, коли обчислення повністю завершено i з'явився результат. Спеціальні старт - i готовність - вузли особливо важливі тоді, коли треба скласти розширену мережу Петрі із наявних елементів.

Суматор

Суматор (рис. 3.11) повинен порахувати маркування від пункту Y до маркувань в Z, тобто створити суму Z+Y. Стартовий вузол на початку операції зайнятий маркуванням “1”. Після перемикання переходу s ця марка зникне з місця старту, а марка у вузлі готовності з'явиться тільки тоді, коли закінчиться процес додавання i сума буде у вузлі Z.

Фініш

 

Z:=Z+Y

 

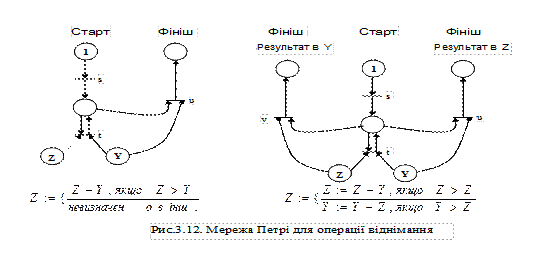
Рис. 3.11. Мережа Петрі як суматор

Після перемикання стартового переходу s маркується середній вузол мережі Петрі. Крок за кроком, перемикаючи перехід t, одне маркування береться з вузла Y (вхід) i одночасно вводиться у вузол Z (вихід). Середній вузол залишається при цьому маркованим, бо він містить у co6i як вихідну, так i вхідну дуги (1-1+1=1). Однак цей вузол не є зайвим, бо він дбає про те, щоб операція додавання відбувалась як результуюча після розблокування стартового вузла. В кінці; операції, коли Y=0, сума з'являється у вузлі Z i перехід t більше не активізується. Для завершення операції призначений перехід u, що тепер активізований; якщо він перемикається, то марка iз середнього вузла виводиться i генерується марка у вузлі готовності, що сигналізує про закінчення обчислення.

Необхідно враховувати, що початкове числове значення Y знищується (у нашому випадку стає нулем) i не може використовуватися для можливих подальших операцій. Якщо змінна Y потрібна для інших операцій, що відбуваються після отримання суми, то мережу Петрі треба будувати так, щоб в ній відновлювалося значення величини Y.

Пристрій для віднімання

Простий пристрій для віднімання (рис.3.12 зліва) можна побудувати iз суматора (рис.3.11), в якому змінено напрямок дуги від Z (штрихова стрілка). На кожному кроці тепер маркування не йде на місце Z, a навпаки, виводиться з Z. Ця методика функціонує тільки за тих умов, що Z³Y; в інших випадках віднімання зупиняється без маркування кінця операції у вузлі готовності. Це, звичайно, не має сенсу, тому на рис.3.12 (праворуч) показано розширений пристрій, який обчислює симетричну різницю.

При симетричному відніманні різниця Z-Y заноситься в Z, якщо Z >Y, а різниця Y-Z заноситься в Y, якщо Y>Z. У зв'язку з цим мережа Петрі доповнюється симетрично переходом v.

Помножувач

Помножувач (рис. 3.13) має складнішу будову, але в переходах s, t i v можна впізнати основні елементи суматора.Це змінює одночасно принцип роботи помножувача: під час кожного проходу Х зменшується на одиницю i Y покроково додається з Z. У вузлі "пам'ять" копіюється початкова величина Y, i в кінці операції через перехід u на Y робиться нова копія, щоб Y можна було використати в наступних розрахунках.

Пам’ять

Z:=Z+X*Y

Рис. 3.13. Мережа Петрі для операції множення

Новий обчислювальний цикл починається, якщо "пам'ять" дорівнює нулю; потім перехід знову активізується через дугу заперечення. Цикли, в яких величина Y додається з Z, виконуються доти, поки Х стане дорівнювати нулю, тобто добуток X*Y буде додано з Z.

На рис.3.14 показано можливість розмноження значень змінної величини. На рис.3.15, 3.16 наведено приклади складних мереж Петрі, як скомпоновані з простіших модулів за методом чорного ящика.

Рис. 3.14. Розмноження значень змінної Х

Послідовні обчислення

Старт Фініш

 

 

Рис. 3.15. Послідовне використання мережі Петрі

 

Паралельні обчислення

Рис. 3.16. Паралельне використання мережі Петрі