
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вправи і завдання до теми №2Содержание книги
Поиск на нашем сайте 1. Паралельна програма виконується на MIMD – системі з 100 процесорами, 3% всіх команд при проході програми виконуються послідовно, а решту може виконуватись паралельно на всіх процесорах. Яке значення має показник прискорення цієї програми на даній програмі? 2. Деяка паралельна програма, що має 10% послідовну частину, має виконуватись на MIMD – системі. Чи існує деякий максимально можливий показник прискорення, незалежний від кількості процесорів системи? 3. Паралельна програма має виконуватись на MIMD – системі з 100 процесорами, проте: - 2% всіх команд при проході програми мають виконуватися послідовно; - 20% всіх команд можуть виконуватись тільки на 50 процесорах. Яке значення має показник прискорення для цієї програми? 4. Паралельна програма має виконуватись на SIMD-системі, що має 10000 процесорних елементів, однак вона містить при виконанні 20% скалярних команд. Решту – векторні команди, що виконуються на всіх ПЕ. Яке значення має показник прискорення для цієї програми? 5. Паралельна програма має виконуватись на SIMD-системі, що має 10000 процесорних елементів. Якщо всі ПЕ були активними впродовж 30% загальної тривалості виконання програми, а решту часу були неактивними, яке значення має показник прискорення для цієї програми? 6. Паралельна програма має виконуватись на SIMD-системі, що має 100 000 процесорних елементів, проте: - 20% всіх виконуваних інструкцій є скалярними командами; - 10% всіх інструкцій можуть виконуватись векторно тільки на 100 процесорах; - 40% всіх інструкцій можуть виконуватись векторно на 50 000 процесорах; - решту інструкцій можуть виконуватись векторно на всіх процесорах. Яке значення має показник прискорення для цієї програми? 7. Чи можна для оцінки продуктивності процесора з рухомою крапкою використовувати одиницю вимірювання MIPS? 8. Чому для оцінки продуктивності паралельних систем неефективний метод обчислення продуктивності складових частин? 9. Які недоліки стосовно обчислення продуктивності має закон Амдала? 10. Як впливають параметри комунікацій на загальну продуктивність систем різного типу?
Тема №3 “Організація мереж Петрі” Питання: Поняття про мережі Петрі Прості мережі Петрі Розширені мережі Петрі Приклади реалізації мереж Петрі Вправи і завдання до теми №3
Поняття про мережі Петрі Мережі Петрі призначені для представлення координації асинхронних подій і застосовуються для описування взаємовідносин між паралельними процесами та їх синхронізацією. Мережа Петрі - це орієнтований, дводольний граф з мітками (марками). Це визначення треба розуміти так (рис.3.1):
На рис.3.2 показано просту мережу Петрі, що має один перехід, три ребра i три вузли, два з яких марковані i один не маркований. Кожен вузол зв'язаний з переходом за допомогою одного ребра.
Прості мережі Петрі Визначення: Активізація (Стан): перехід t активізований, якщо всі вхідні вузли pi цього переходу марковані. Тобто, активізація - це залежна від часу властивість переходу i описує деякий стан. Перехід мережі Петрі на рис.3.2 активізований, бо обидва вузли ребер, що входять у перехід, марковані. Ввімкнення (Подія): активізований перехід t може вмикатися. Тоді зникають марки з вcix вхідних вузлів pi переходу t i маркуються всі вихідні вузли pj цього переходу. Процес увімкнення переходу має передумовою його активізацію. Як видно з рис.3.3, в процесі ввімкнення відбувається зміна маркування вузлів мережі Петрі: перехід активізований, бо обидва вузли вхідних ребер марковані. Після ввімкнення переходу маркування обох верхніх (вхідних) вузлів зникає, в той час як на нижньому (вихідному) вузлі з'являється нова марка. Загальна кількість маркувань у будь-якій мережі Петрі не залишається постійною. Якби на вихідному вузлі вже була марка, то вона б переписалася, тобто вузол як i раніше був би зайнятий маркою.
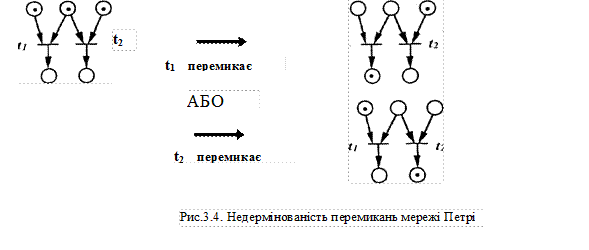
Невизначеність: якщо одночасно активізовані декілька переходів, то не зрозуміло, який з них перемкнеться першим. Зроблені вище визначення не дають уявлення про порядок перемикання декількох активізованих переходів. Одночасне перемикання їх неможливе! Як показано на рис.3.4, у цьому випадку можуть відбуватися два процеси i який з них фактично має місце, в мережі Петрі визначити не можна. У зв'язку з тим, що ввімкнення одного або іншого переходу не може бути здійснене за допомогою зовнішніх параметрів, мережа Петрі має в цьому випадку невизначеність. Стан: стан маркування (або, коротко, стан) мережі Петрі до деякого моменту часу Т визначено як сукупність маркувань кожного окремого вузла мережі.
У простих мережах Петрі стан маркування можна відобразити за допомогою деякої послідовності бінарних цифр (двійковий рядок). Можливе перемикання переходу задається за допомогою переходу в послідовність стану (якщо за аналогією з показаним на рис.3.4 можуть перемикатися декілька переходів, то існують різноманітні можливі послідовності станів):
У тому випадку, коли перемикання кожного переходу визначається цим правилом, всі послідовності станів одного заданого початкового стану можуть бути “обчислені” комп'ютером i можуть бути розпізнані вірогідні блокування. Генерування марок: перехід, що не має жодного вхідного ребра, завжди активізований i може постійно видавати нові марки на вихідні вузли, що з’єднані з ним. Знищення марок: перехід, що не має жодного вихідного ребра i має тільки одне вхідне ребро, завжди активізований тоді, коли це місце марковано i він може постійно знищувати марку. “Мертвий" стан: Мережа Петрі перебуває в "мертвому" стані (блокована), якщо жоден з переходів не активізований.
Блокована мережа Петрі є статичною, тобто в ній немає нових послідовностей станів. Наприклад, обидві мережі Петрі, що показані на рис.3.4, блоковані. “Живий” стан: мережа Петрі перебуває в "живому" стані (не блокована в жодному моменті часу), якщо хоча б один з її переходів активізований i це справедливо також для кожного наступного стану. Зауважимо, що "живий" стан не є протилежністю "мертвого" стану. Мережа Петрі в "живому" стані не блокована i не перебуває в жодному із можливих послідовностей станів, в той час як не блокована мережа Петрі не обов'язково має бути в "живому" стані. Наприклад, блокування може відбутися тільки після багатьох послідовних кроків. На рис. 3.6 показано два приклади мереж. Ліва мережа Петрі (рис.3.6) є "живою" тому, що її маркування змінюється від одного вузла до іншого, але не зникає; перехід завжди тут активізований. В правій мережі Петрі можуть перемикатись або перехід и (i тоді мережа негайно переходить у "мертвий" стан), або перехід s. Нарешті можуть перемикатись один раз переходи t i U, що веде також до "мертвого" стану мережі Петрі. За допомогою мереж Петрі можна уникнути взаємоблокування процесів або виникнення суперечних даних у тих випадках, коли два процеси мають звернутися до однієї і тієї області даних (рис.3.7).
Рис. 3.6. Діюча та блокуюча мережі Петрі
Процес P1 (виробник) генерує тут незалежно від процесу P2 дані, записує їх у буферну область пам'яті i хоче без затримки працювати далі. Процес P2 (споживач) читає дані із цього буфера i використовує їх паралельно з процесом P1. Щоб уникнути суперечливих даних треба виконати таку умову: одночасний доступ процесів в одну і ту саму область пам'яті має бути виключений. Це викликає потребу в синхронізації процесів, тобто один з них має деякий час почекати. На рис.3.8 показано простий приклад для випадку, коли процеси P1 та P2 мають бути синхронізовані, тому, що вони, наприклад, хочуть користуватися одними і тими самими даними.
P1 - семафор Рис. 3.8. Мережа Петрі для синхронізації процесів Кожний процес має тут два стани - активний i пасивний, які символізуються двома вузлами. Процес перебуває в тому стані, який позначається відповідною маркою (на рис.3.8 обидва процеси пасивні). Кожен з двох процесів може змінювати свій стан з пасивного на активний i навпаки, перемикаючи відповідний перехід. Обидва цикли стану для P1 i P2 аналогічні простому контуру, що зображений зліва на рис.3.6, але ці цикли пов'язані між собою за допомогою семафора S. Процес, що хотів би змінити свій стан з пасивного на активний (щоб звернутися до загальних даних), потребує для цього переходу маркування в S. Це означає, що він тільки тоді може змінити свій стан на активний, коли марка семафора не використовується іншим процесом (який в цей час перебуває в активному стані). При переході в активний стан семафор S звільняється від маркування; у тому випадку, коли інший процес запросить перехід з пасивного стану в активний (доступ до загальних даних), він має чекати, поки перший процес не перейде знову зі стану активного в пасивний i знову з'явиться семафор-марка S. Синхронізація за допомогою цієї мережі Петрі є високонадійною, оскільки, в кожний момент часу тільки один процес перебуває в активному стані. Таким чином, в разі одночасного запиту процеси з паралельних перетворюються в послідовні i їх блокування виникнути не зможе. Розширені мережі Петрі За допомогою трьох простих розширень прості мережі Петрі стають суттєво продуктивнішими.Як показано Хопкрофтом i Ульманом, "розширені мережі Петрі” (навіть без додатково введених нижче ваг дуг) за своєю ефективністю рівні машині Тьюрінга, тобто вони можуть застосовуватись як загальна модель обчислюваності. Розширення: Багаторазове маркування.
- перехід активізований тільки тоді, коли число, що відповідає кількості маркувань кожного його вхідного вузла, є більшим чи дорівнює одиниці; - якщо активізований перехід перемикається, то числа-маркування ycix вхідних вузлів цього переходу зменшуються, а ycix вихідних вузлів - збільшуються на одиницю. Тобто кількість маркувань одного вузла може бути як завгодно великою, але відповідне число не може бути меншим від нуля. Дуги-заперечення Дуги-заперечення в мережах Петрі зображаються кружечком на кінці замість стрілки (рис.3.9) i не мають дугової ваги; дуги, що були визначені раніше, розглядаються як позитивні.
Рис. 3.9. Дуга-заперечення Вони завжди направлені тільки від деякого вузла до деякого переходу, зворотного напрямку не дозволяється. Введення дуг-заперечень зумовлює оновлені пристосування правил активізації та перемикань: - перехід активізований тільки тоді, коли кількість маркувань кожного вхідного вузла з позитивною дугою більша або дорівнює одиниці i коли кількість маркувань кожного вхідного вузла з дугою-запереченням дорівнює нулю (на рис.3.9 перехід t активізований, якщо P1 маркований i P2 не маркований); - якщо активізований перехід перемикається, то кількість маркувань ycix вхідних вузлів з позитивними дугами цього переходу зменшується на одиницю, в той час як кількість маркувань вхідних вузлів з дугами-запереченнями залишається незмінною. Числа, що відповідають кількості маркувань ycix вихідних вузлів, як i раніше, збільшуються на одиницю. Вага дуг Кожна дуга, що не є дугою-запереченням, може мати постійну цілочислову вагу, що більша або дорівнює одиниці (число, що використовується за замовчанням, рис. 3.10). Для активізації i перемикання переходу діє правило: - перехід активізований тільки тоді, коли кількість маркувань кожного його вхідного вузла більша або дорівнює відповідній вазі дуги, а для дуги-заперечення дорівнюють нулю; - при перемиканні переходу кількість маркувань кожного вхідного вузла зменшується на вагу відповідної вхідної дуги (вона залишається незмінною для дуг-заперечень); кількість маркувань кожного вихідного вузла збільшується на вагу відповідної вихідної дуги.
|
|||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |


 Кожна мережа Петрі є графом з двома різними групами вершин: вузли та переходи. Між вузлами та переходами можуть міститися орієнтовані ребра (дуги), але два вузли або два переходи не можуть з’єднуватися ребрами. Між кожною парою вузол/перехід може існувати максимально одне ребро від вузла до переходу (ребро входу) i максимально одне ребро від переходу до вузла (ребро виходу). Вузли можуть бути вільними або зайнятими міткою (маркованими); переходи не можуть бути маркованими. Вузли, що є стартовими пунктами одного ребра до одного переходу t, називаються далі вхідними вузлами переходу t. Вузли, що є кінцевими пунктами ребра від переходу t називаються вихідними вузлами переходу t.
Кожна мережа Петрі є графом з двома різними групами вершин: вузли та переходи. Між вузлами та переходами можуть міститися орієнтовані ребра (дуги), але два вузли або два переходи не можуть з’єднуватися ребрами. Між кожною парою вузол/перехід може існувати максимально одне ребро від вузла до переходу (ребро входу) i максимально одне ребро від переходу до вузла (ребро виходу). Вузли можуть бути вільними або зайнятими міткою (маркованими); переходи не можуть бути маркованими. Вузли, що є стартовими пунктами одного ребра до одного переходу t, називаються далі вхідними вузлами переходу t. Вузли, що є кінцевими пунктами ребра від переходу t називаються вихідними вузлами переходу t.





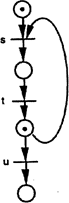 Не діюча, блокує через декілька кроків
Не діюча, блокує через декілька кроків
 Діюча
Діюча







